6.2.2: Parábolas y la Fórmula de Distancia
- Page ID
- 108873
Parabolas y la Fórmula de Distancia
En lecciones anteriores sobre secciones cónicas, discutimos tanto el círculo como la elipse, cada uno de los cuales resulta de “cortar” un cono transparente de izquierda a derecha. En esta lección, discutiremos la forma que se forma cuando cortamos solo un lado del cono, creando una figura en forma de cuenco llamada parábola.
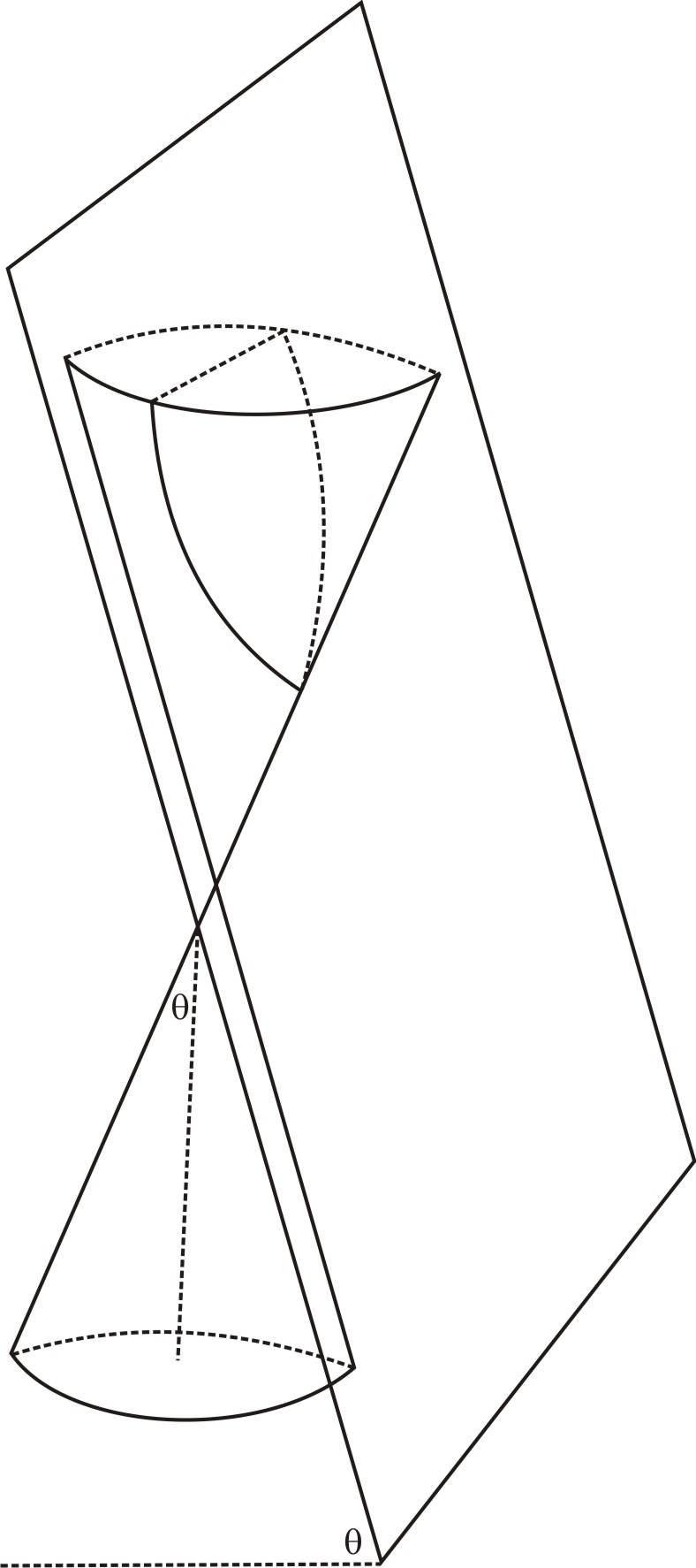
Considera la figura de “reloj de arena” que usamos en las definiciones de círculo y elipse, creada al conectar dos conos infinitos en sus puntas. ¿Qué limitación habría en el ángulo de la rebanada que sacaríamos de uno de los conos, si solo quisiéramos obtener una parábola (no conseguir una elipse, y no golpear el otro cono de ninguna manera)?
Parabolas y la Fórmula de Distancia
Hemos examinado elipses y círculos, los dos casos en los que un plano cruza solo un lado del cono y crea una sección transversal finita. ¿Es posible que un plano intersecta solo un lado del cono, pero cree una sección transversal infinita?
Resulta que esto es posible si y sólo si el plano es paralelo a una de las líneas que componen el cono. O, en otras palabras, el ángulo entre el plano y el horizonte, es igual al ángulo formado por un lado del cono y el plano horizontal.

En la imagen de arriba, si inclinas un poco el avión hacia la izquierda cortará una elipse finita (posiblemente una muy grande si solo la inclinas un poco). Incline el plano hacia la derecha y éste cruzará ambos lados del cono, haciendo una sección cónica de dos partes llamada hipérbola, que se discutirá en la siguiente sección.
Cuando el plano es paralelo a desde el lado del cono, la forma infinita que resulta de la intersección del plano y el cono se llama parábola. Al igual que la elipse, tiene una serie de interesantes propiedades geométricas.
La ecuación de una parábola es más simple que la de la elipse. Existen un par de métodos para derivar la ecuación de una parábola, en esta lección exploramos la fórmula de distancia.
Este primer método surge directamente de la propiedad focus - directrix discutida en la sección anterior. Supongamos que tenemos una línea y un punto no en esa línea en un plano, y queremos encontrar la ecuación del conjunto de puntos en el plano que es equidistante a estos dos objetos. Sin perder generalidad alguna, podemos orientar la línea horizontalmente y el punto en el eje y, con el origen a medio camino entre ellos. Dado que la parábola es el conjunto de puntos equidistantes de la línea y el punto, La parábola pasa por el origen, (0, 0). La siguiente imagen muestra esta configuración. El punto directamente entre la directriz y el foco (el origen en este caso) se denomina vértice de la parábola. Supongamos que el foco se encuentra en (0, b). Entonces la directriz debe ser y=−b.
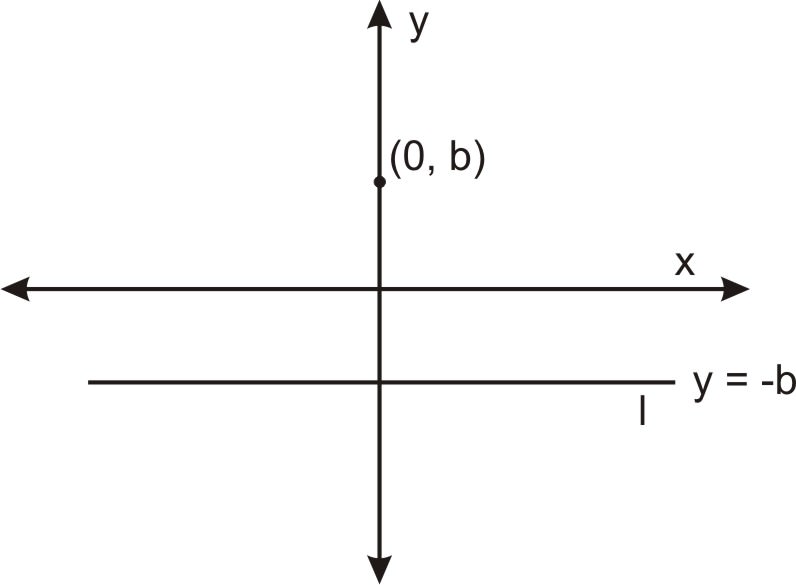
Así, la parábola es el conjunto de puntos\(\ (x, y)\) equidistantes de la línea\(\ y=-b\) y el punto de enfoque\(\ (0, b)\). La distancia a la línea es el segmento vertical de\(\ (x, y)\) abajo a\(\ (0,-b)\), que tiene longitud\(\ y-(-b)=y+b\). La distancia desde\(\ (x, y)\) el foco\(\ (0, b)\) es\(\ \text { distance }=\sqrt{(x-0)^{2}+(y-b)^{2}}\) por la fórmula de distancia. Entonces la ecuación de la parábola es el conjunto de puntos donde estas dos distancias igualan.
\(\ y+b=\sqrt{(x-0)^{2}+(y-b)^{2}}\)
Dado que las distancias son siempre positivas, podemos cuadrar ambos lados sin perder ninguna información, obteniendo lo siguiente.
\ (\\ comenzar {alineado}
y^ {2} +2 b y+b^ {2} &=x^ {2} +y^ {2} -2 b y+b^ {2}\\
2 b y &=x^ {2} -2 b y\\
4 b y &=x^ {2}\\
y &=\ frac {1} {4 b} x^ {2}
\ fin alineado}\)
Pero\(\ b\) fue elegido arbitrariamente y podría haber sido cualquier número positivo, y para cualquier número positivo\(\ a\),, siempre existe un número\(\ b\) tal que\(\ a=\frac{1}{4 b}\), así podemos reescribir esta ecuación como:
\(\ y=a x^{2}\)
donde\(\ a\) hay alguna constante.
Esta es la forma general de una parábola con una directriz horizontal, con un foco tendido por encima de ella, y con un vértice en el origen. Si\(\ a\) es negativo, la parábola se refleja alrededor del\(\ x\) eje −, dando como resultado una parábola con una directriz horizontal, con un foco debajo de ella, y con un vértice en el origen. La ecuación se puede desplazar horizontal o verticalmente moviendo el vértice, dando como resultado la forma general de una parábola con una directriz horizontal y pasando por un vértice de\(\ (h,k)\):
\(\ y-k=a(x-h)^{2}\)
Conmutación\(\ x\) y\(\ y\), la ecuación para una parábola con una directriz vertical y con un vértice en\(\ (h,k)\) es:
\(\ x-h=a(y-k)^{2}\)
Ejemplos
Anteriormente, te hicieron una pregunta sobre la limitación en el ángulo de la rebanada sacada de uno de los conos si solo querías una parábola.
Solución
Para obtener solo una sección transversal de parábola, la rebanada debe tomarse en el mismo ángulo que el lado del cono, de esa manera el borde de la rebanada corre paralelo al borde del cono y nunca la cruza en la parte superior o inferior.
Esto se puede ver con una mirada cercana a la imagen desde arriba:

Esboza una gráfica de la parábola\(\ y=3 x^{2}+12 x+17\).
Solución
Primero, necesitamos factorizar el coeficiente del\(\ x^{2}\) término y completar el cuadrado:
\ (\\ begin {array} {l}
y=3\ izquierda (x^ {2} +4 x\ derecha) +17\\
y=3\ izquierda (x^ {2} +4 x+4\ derecha) +17-12\\
y=3 (x+2) ^ {2} +5
\ end {array}\)
Ahora lo escribimos en la forma\(\ y-k=a(x-h)^{2}\):
\(\ y-5=3(x+2)^{2}\)
Entonces el vértice está en (−2, 5) y trazando algunos x−valores a cada lado de x=−2, podemos dibujar el siguiente boceto de la parábola:
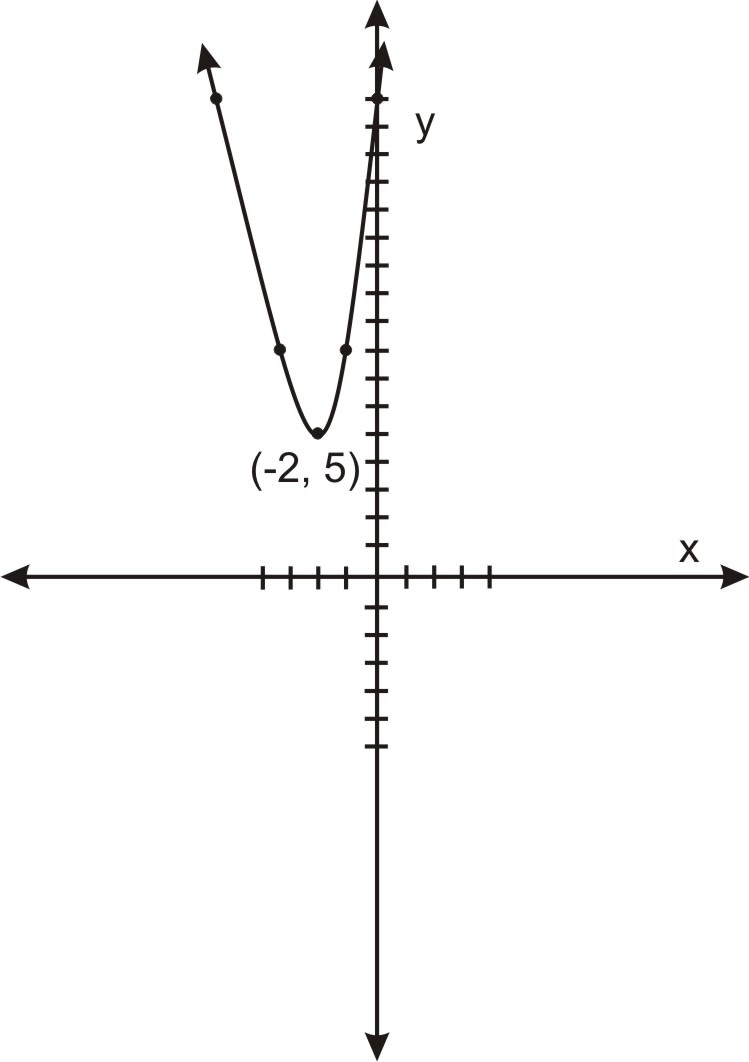
Esboce una gráfica de la siguiente parábola:\(\ y=2 x^{2}-2 x-3\).
Solución
Factorizar el 2:\(\ y=2\left(x^{2}-x\right)-3\)
Completa el cuadrado:\(\ y+\frac{1}{2}=2\left(x^{2}-x+\frac{1}{4}\right)-3\)
Agrega 3 a ambos lados y factoriza el trinomio:\(\ y+3 \frac{1}{2}=2\left(x-\frac{1}{2}\right)^{2}\)
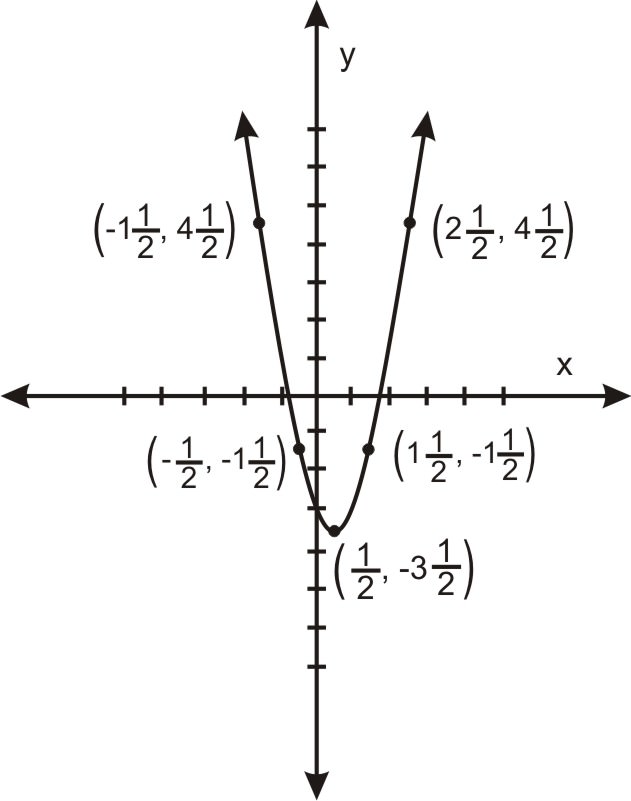
El vértice\(\ (h, k)\) es:\(\ \left(\frac{1}{2},-3 \frac{1}{2}\right)\)
Traza un par de puntos para obtener:
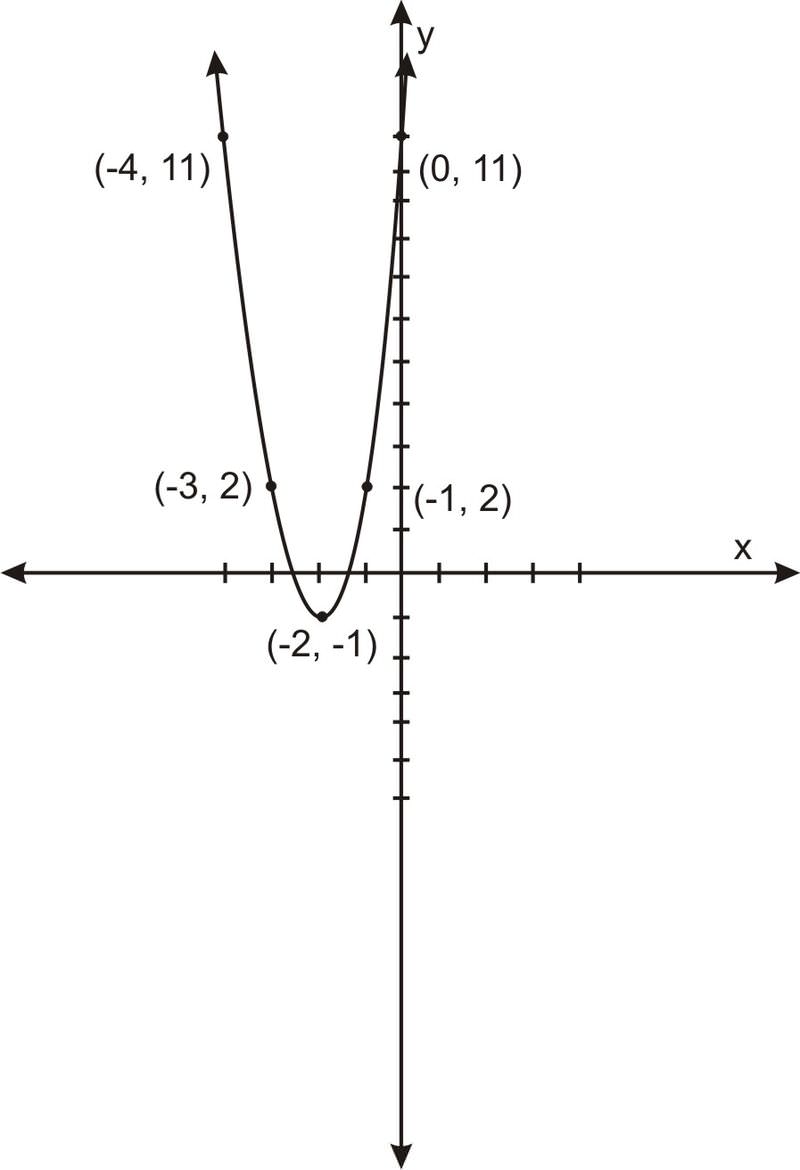
Esboce una gráfica de la siguiente parábola:\(\ 3 x^{2}+12 x+11-y=0\).
Solución
Factorizar el 3 y mover y y 11:\(\ 3\left(x^{2}+4 x\right)=y-11\)
Completa el cuadrado:\(\ 3\left(x^{2}+4 x+4\right)=y-11+12\)
Factorizar el trinomio y recopilar términos similares:\(\ 3(x+2)^{2}=y+1\)
El vértice\(\ (h, k)\) está en:\(\ (-2,-1)\)
Traza un par de puntos para obtener:
Identificar cuáles de las siguientes ecuaciones son parábolas:
- \(\ y-5 x+x^{2}=3\)
- \(\ x^{2}-3 y^{2}+3 y-2 x+15=0\)
- \(\ x-6 y^{2}+20 x-100=0\)
Solución
Recordemos que una parábola solo tiene un término de entrada cuadrado:
Dado que\(\ \text { b. } x^{2}-3 y^{2}+3 y-2 x+15=0\) es cuadrado en la entrada y salida (en otras palabras, ambos\(\ x\) y\(\ y\) son cuadrados), no es una parábola.
\(\ \text { a. } y-5 x+x^{2}=3\)y ambas\(\ \text { c. } x-6 y^{2}+20 x-100=0\) son parábolas.
Por cierto, después de completar el cuadrado, la ecuación a factores como:
\(\ (x-1)^{2}-3\left(y-\frac{1}{2}\right)^{2}+14 \frac{3}{4}=0\).
Calcula la distancia entre (3, 4) y (9, 5).
Solución
Para calcular la distancia entre (3, 4) y (9, 5), usa la fórmula de distancia
\(\ \text { distance }=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
\(\ \text { distance }=\sqrt{(9-3)^{2}+(5-4)^{2}} \ldots . . \text { Substitute }\)
\(\ \text { distance }=\sqrt{(6)^{2}+(1)^{2}} \ldots . . \text { Simplify }\)
\(\ \text { distance }=\sqrt{36+1} \rightarrow \sqrt{37}\)
\(\ \therefore \sqrt{37}\)es la distancia entre (3, 4) y (9, 5).
Calcula la distancia entre (-2, 7) y (11, 23).
Solución
Para calcular la distancia entre (-2, 7) y (11, 23), usa la fórmula de distancia
\(\ \text { distance }=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
\(\ \text { distance }=\sqrt{(11-(-2))^{2}+(23-7)^{2}} \ldots . . \text { Substitute }\)
\(\ \text { distance }=\sqrt{(13)^{2}+(16)^{2}} \ldots . . \text { Simplify }\)
\(\ \text { distance }=\sqrt{169+256} \rightarrow \sqrt{425} \rightarrow 5 \sqrt{17}\)
\(\ \therefore 5 \sqrt{17}\)es la distancia entre (-2, 7) y (11, 23).
Revisar
Grafique lo siguiente:
- \(\ y=-3(x-1)^{2}+2\)
- \(\ y=3(x-1)^{2}-1\)
- \(\ x=-2(y+2)^{2}-1\)
- \(\ y=3(x+4)^{2}-1\)
- \(\ y=(x-3)^{2}\)
- \(\ x=-3(y)^{2}+1\)
- \(\ x=-(y-3)^{2}-4\)
- \(\ x=-3(y-4)^{2}+4\)
- \(\ y=2(x+3)^{2}-3\)
- \(\ x=(y-1)^{2}-2\)
Para las preguntas 11-20, imagínese un cono limitado (no infinitamente alto), como se muestra a continuación. Supongamos que las dos coordenadas enumeradas representan la intersección de una curva parabólica y la parte superior del cono. Si la superficie superior del cono estuviera representada por el eje x, entonces las dos coordenadas podrían considerarse las intercepciones x de la ecuación de la parábola. Encuentra la distancia entre los puntos, y donde sea necesario, las coordenadas de los puntos.
- Coordenadas: (-20, -17) y (6, -1)
- Coordenadas: (-1, -5) y (6, -13)
- Coordenadas: (1, 2) y (5, -5)
- Coordenadas: (13, 12) y (15, 6)
- Coordenadas: (3, 9) y (6, -14)
- \(\ -25 x^{2}+15 x+10=0\)
- \(\ -24 x^{2}+22 x-4=0\)
- \(\ 4 x^{2}-24 x+32=0\)
- \(\ 24 x^{2}+54 x+27=0\)
- \(\ 12 x^{2}+25 x+12=0\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.3.
El vocabulario
| Término | Definición |
|---|---|
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| directrix | La directriz de una parábola es la línea de la que parece apartarse la parábola. Todos los puntos en una parábola son equidistantes del foco de la parábola y la directriz de la parábola. |
| Fórmula de distancia | La distancia entre dos puntos\(\ \left(x_{1}, y_{1}\right)\) y se\(\ \left(x_{2}, y_{2}\right)\) puede definir como\(\ d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\). |
| Elipse | Las elipses son secciones cónicas que parecen círculos alargados. Una elipse representa todas las ubicaciones en dos cotas que están a la misma distancia de dos puntos especificados llamados focos. |
| Elipses | Las elipses son secciones cónicas que parecen círculos alargados. Una elipse representa todas las ubicaciones en dos cotas que están a la misma distancia de dos puntos especificados llamados focos. |
| enfoque | El foco de una parábola es el punto que “ancla” una parábola. Cualquier punto de la parábola está exactamente a la misma distancia del foco que de la directriz. |
| Parábola | Una parábola es el conjunto de puntos que son equidistantes de un punto fijo en el interior de la curva, llamado el “'foco"', y una línea en el exterior, llamada la “'directrix"'. La directriz es vertical u horizontal, dependiendo de la orientación de la parábola. |
| Vertex | El vértice de una parábola es el punto más alto o más bajo en la gráfica de una parábola. El vértice es el punto máximo de una parábola que se abre hacia abajo y el punto mínimo de una parábola que se abre hacia arriba. |

