6.2.1: Parábolas con vértice en el origen
- Page ID
- 108855
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Parabolas con Vertex en el Origen
El área de un cuadrado está representada por la ecuación\(\ y=9 x^{2}\). ¿Cuáles son el foco y directrix de esta ecuación?
Parabolas con Vertex en el Origen
Ya sabes que la gráfica de una parábola tiene la gráfica padre\(\ y=x^{2}\), con un vértice de (0, 0) y un eje de simetría de\(\ x = 0\). Una parábola también se puede definir de una manera diferente. Tiene una propiedad tal que cualquier punto en él es equidistante de otro punto, llamado foco, y una línea llamada directrix.
El foco está en el eje de simetría y el vértice está a medio camino entre éste y la directrix. La directrix es perpendicular al eje de simetría.
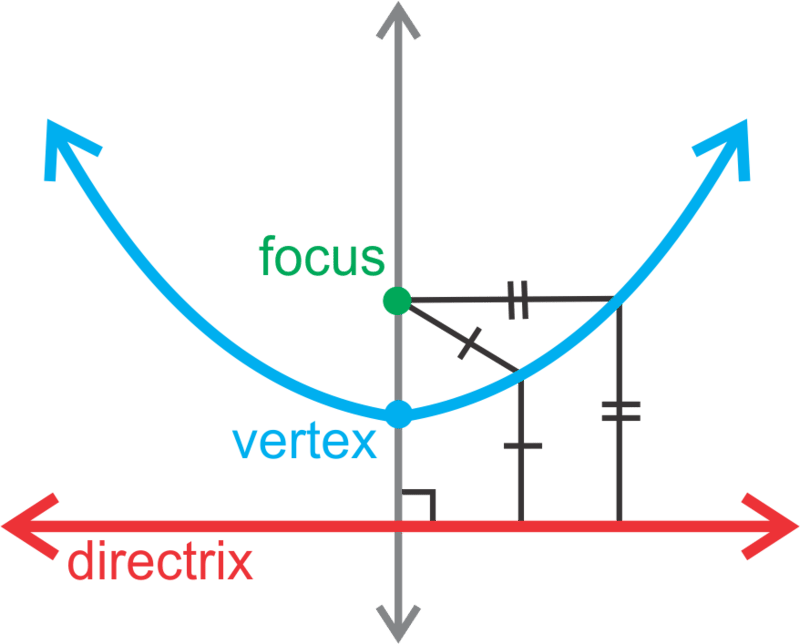
Hasta ahora, nos hemos acostumbrado a ver la ecuación de una parábola como\(\ y=a x^{2}\). En este concepto, reescribiremos la ecuación para que parezca\(\ x^{2}=4 p y\) dónde\(\ p\) se usa para encontrar el foco y la directrix. También dibujaremos la parábola con una orientación horizontal, tal que la ecuación será\(\ y^{2}=4 p x\).
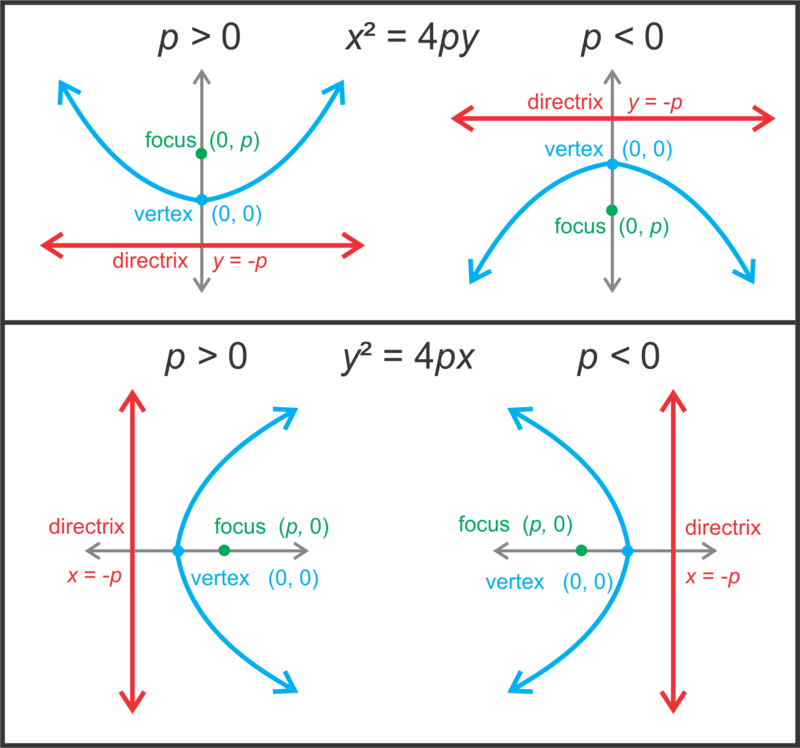
Observe, que cuando la parábola se abre a la izquierda o a la derecha, la y es cuadrada. En este concepto, el vértice será (0, 0).
Analicemos la ecuación\(\ y^{2}=-12 x\). Encontraremos el foco, directrix, y determinaremos si la función se abre hacia arriba, hacia abajo, hacia la izquierda o hacia la derecha. Entonces, graficaremos la parábola.
Para encontrar el enfoque y la directrix, necesitamos encontrar\(\ p\). Podemos establecer\(\ -12=4 p\) y resolver para\(\ p\).
\ (\\ begin {array} {c}
-12&=4 p\\
-3&=p
\ end {array}\)
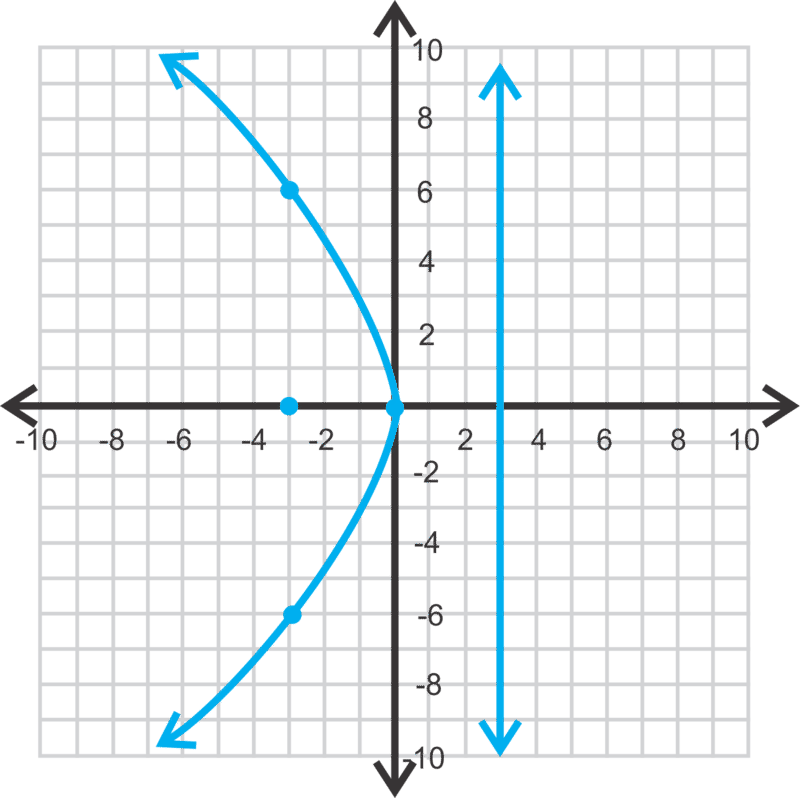
Porque\(\ y\) es cuadrada, sabemos que la parábola se abre a la izquierda o a la derecha. Porque\(\ p\) es negativo, sabemos que se va a abrir hacia la izquierda, hacia el lado negativo del eje x. Usando las imágenes de arriba, esta parábola es como la segunda debajo\(\ y^{2}=4 p x\). Por lo tanto, el foco es (−3, 0) y la directrix es x=3. Para graficar la parábola, trazar el vértice, enfocar, directrix y bosquejar la curva. Encuentre al menos uno o dos puntos en la curva para asegurarse de que su boceto sea preciso. Por ejemplo, porque (−3, 6) está en la parábola, entonces (−3, −6) también está en la parábola porque es simétrica.
Observe que los puntos (−3, 6) y (−3, −6) son equidistantes del foco y la directrix. Ambos son 6 unidades de cada uno.
El foco de una parábola es\(\ \left(0, \frac{1}{2}\right)\). Encontremos la ecuación de la parábola.
Debido a que el\(\ p\) valor es el valor y y positivo, esta parábola se va a abrir. Entonces, la ecuación general es\(\ x^{2}=4 p y\). Conectando\(\ \frac{1}{2}\) para\(\ p\), tenemos\(\ x^{2}=4 \cdot \frac{1}{2} y\) o\(\ x^{2}=2 y\).
Ahora, encontremos la ecuación de la parábola a continuación.
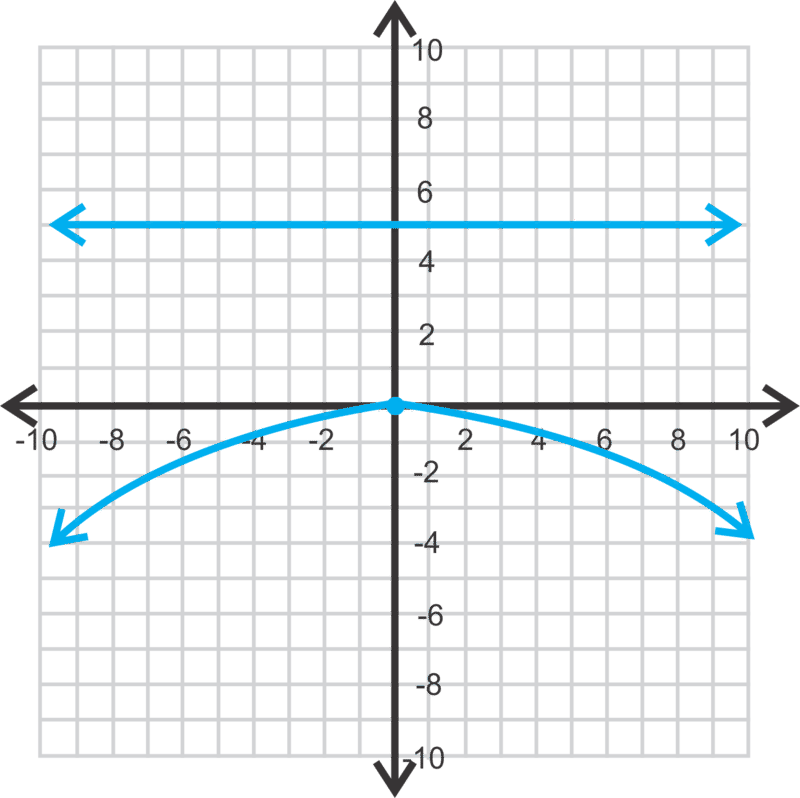
La ecuación de la directrix es\(\ y=5\), lo que significa que\(\ p=-5\) y la ecuación general será\(\ x^{2}=4 p y\). Conectando -5 para\(\ p\), tenemos\(\ x^{2}=-20 y\).
Ejemplos
Anteriormente, se le pidió que encontrara el foco y directrix de la ecuación\(\ y=9 x^{2}\).
Solución
Para encontrar el enfoque y la directrix, necesitamos resolver para\(\ x^{2}\) y luego encontrar\(\ p\).
\ (\\ begin {array} {l}
y&=9 x^ {2}\
\ frac {1} {9} y&=x^ {2}
\ end {array}\)
Ahora podemos establecer\(\ \frac{1}{9}=4 p\) y resolver para\(\ p\).
\ (\\ begin {array} {l}
\ frac {1} {9} =4 p\\
\ frac {1} {36} =p
\ end {array}\)
Por lo tanto, el foco es\(\ \left(0, \frac{1}{36}\right)\) y la directrix es\(\ y=-\frac{1}{36}\).
Determinar si la parábola\(\ x^{2}=-2 y\) se abre hacia arriba, abajo, izquierda o derecha.
Solución
Abajo;\(\ p\) es negativo y\(\ x\) es cuadrado.
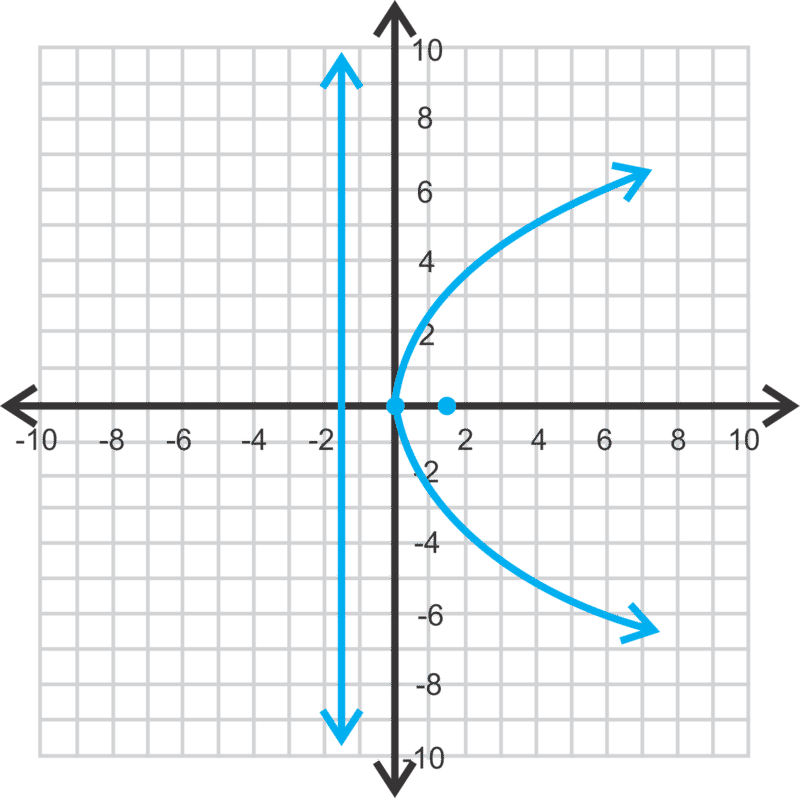
Encuentra el enfoque y la directrix de\(\ y^{2}=6 x\). Después, grafica la parábola.
Solución
Resolviendo para\(\ p\), tenemos\(\ 4 p=6 \rightarrow p=\frac{3}{2}\). Porque\(\ y\) es cuadrado y\(\ p\) es positivo, la parábola se abrirá a la derecha. El foco es\(\ \left(\frac{3}{2}, 0\right)\) y la directrix es\(\ x=-\frac{3}{2}\).
Encuentra la ecuación de la parábola con directrix\(\ x=-\frac{3}{8}\).
Solución
Si la directrix es negativa y vertical (x=), sabemos que la ecuación va a ser\(\ y^{2}=4 p x\) y la parábola se abrirá hacia la derecha, haciendo\(\ p\) positiva;\(\ p=\frac{3}{8}\). Por lo tanto, la ecuación será\(\ y^{2}=4 \cdot \frac{3}{8} \cdot x \rightarrow y^{2}=\frac{3}{2} x\).
Revisar
Determinar si la parábola se abre a la izquierda, derecha, arriba o abajo.
- \(\ x^{2}=4 y\)
- \(\ y^{2}=-\frac{1}{2} x\)
- \(\ x^{2}=-y\)
Encuentra el foco y directrix de las siguientes parábolas.
- \(\ x^{2}=-2 y\)
- \(\ y^{2}=\frac{1}{4} x\)
- \(\ y^{2}=-5 x\)
Grafica las siguientes parábolas. Identificar el enfoque y directrix también.
- \(\ x^{2}=8 y\)
- \(\ y^{2}=\frac{1}{2} x\)
- \(\ x^{2}=-3 y\)
Encuentra la ecuación de la parábola dado que el vértice es (0, 0) y el foco o directrix.
- enfoque: (4, 0)
- directrix: x=10
- enfoque:\(\ \left(0, \frac{7}{2}\right)\)
- Usted ha visto que antes la ecuación parabólica básica era\(\ y=a x^{2}\). Ahora, escribimos\(\ x^{2}=4 p y\). Reescribir\(\ p\) en términos de\(\ a\) y determinar cómo se afectan entre sí.
- Desafío Usa la fórmula de distancia\(\ d=\sqrt{\left(x_{2}-x_{1}\right)^{2}-\left(y_{2}-y_{1}\right)^{2}}\),, para demostrar que el punto (4, 2) está en la parábola\(\ x^{2}=8 y\).
- Aplicación del mundo real Una antena parabólica es una parábola tridimensional que se utiliza para recuperar sonido, TV u otras ondas. Suponiendo que el vértice es (0, 0), ¿dónde tendría que estar el foco en una antena parabólica de 4 pies de ancho y 9 pulgadas de profundidad? Se puede suponer que la parábola tiene una orientación vertical (se abre).
Respuestas para problemas de revisión
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.1.
El vocabulario
| Término | Definición |
|---|---|
| directrix | La directrix de una parábola es la línea de la que parece desviarse la parábola. Todos los puntos en una parábola son equidistantes del foco de la parábola y la directrix de la parábola. |
| enfoque | El foco de una parábola es el punto que “ancla” una parábola. Cualquier punto de la parábola está exactamente a la misma distancia del foco que de la directrix. |
| Parábola | Una parábola es el conjunto de puntos que son equidistantes de un punto fijo en el interior de la curva, llamado el “'foco"', y una línea en el exterior, llamada la “'directrix"'. La directrix es vertical u horizontal, dependiendo de la orientación de la parábola. |
Atribuciones de imagen
- [Figura 1]
Crédito: Holly Fischer
Fuente: https://commons.wikimedia.org/wiki/File:Three_Main_Layers_of_the_Eye.png
Licencia: CC BY-NC 3.0