2.6: Conjeturas y contraejemplos

Última actualización
Guardar como PDF

Page ID: 107396

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Conjeturas y ejemplos educados que los desacreditan.

Una conjetura es una “suposición educada” que se basa en ejemplos en un patrón. Un contraejemplo es un ejemplo que desmiente una conjetura.

Supongamos que se le dio un patrón matemático como\(h = \dfrac{−16}{t^2}\). ¿Y si quisieras hacer una conjetura educada, o conjetura, sobre\(h\)?

Utilice la siguiente información para los Ejemplos 1 y 2:

Un vendedor de autos vendió 5 autos usados a cinco parejas diferentes. Se percató de que cada pareja tenía menos de 30 años. Al día siguiente, vendió un auto nuevo de lujo a una pareja de unos 60 años El vendedor determinó que solo las parejas más jóvenes por autos usados.

Ejemplo\(\PageIndex{1}\)

¿Es lógica la conjetura del vendedor? ¿Por qué o por qué no?

Solución

Es lógico basado en sus experiencias, pero no es cierto.

Ejemplo\(\PageIndex{2}\)

¿Se te ocurre un contraejemplo?

Solución

Un contraejemplo sería una pareja que tiene 30 años o más comprando un auto usado.

Ejemplo\(\PageIndex{3}\)

Aquí hay una ecuación algebraica y una tabla de valores para\(n\) y\(t\).

\(t=(n−1)(n−2)(n−3)\)

\(n\)	\((n−1)(n−2)(n−3)\)	\(t\)
\ (n\)” class="lt-k12-2141">1	\ ((n−1) (n−2) (n−3)\)” class="lt-k12-2141">\((0)(−1)(−2)\)	\ (t\)” class="lt-k12-2141">0
\ (n\)” class="lt-k12-2141">2	\ ((n−1) (n−2) (n−3)\)” class="lt-k12-2141">\((1)(0)(−1)\)	\ (t\)” class="lt-k12-2141">0
\ (n\)” class="lt-k12-2141">3	\ ((n−1) (n−2) (n−3)\)” class="lt-k12-2141">\((2)(1)(0)\)	\ (t\)” class="lt-k12-2141">0

Solución

Después de mirar la mesa, Pablo hace esta conjetura:

El valor de\((n−1)(n−2)(n−3)\) es 0 para cualquier número n.

¿Es esta una verdadera conjetura?

Esta no es una conjetura válida. Si Pablo continuara la tabla a n=4, habría visto que\((n−1)(n−2)(n−3)=(4−1)(4−2)(4−3)=(3)(2)(1)=6\)

En este ejemplo\(n=4\) está el contraejemplo.

Ejemplo\(\PageIndex{4}\)

Arthur está haciendo figuras para un proyecto de arte. Dibujó polígonos y algunas de sus diagonales.

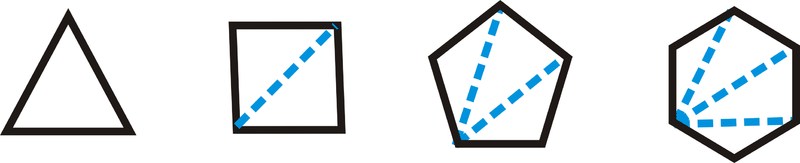
f-d_1a8e170aaf8620eaf6b280adec82dced4a1087956f5ea32a28204c7f+image_tiny+image_tiny.png — Figura\(\PageIndex{1}\)

A partir de estos ejemplos, Arthur hizo esta conjetura:

Si un polígono convexo tiene\(n\) lados, entonces hay\(n−2\) triángulos formados cuando se dibujan diagonales desde cualquier vértice del polígono.

¿Es correcta la conjetura de Arthur? O bien, ¿puedes encontrar un contraejemplo?

Solución

La conjetura parece ser correcta. Si Arthur dibuja otros polígonos, en todos los casos podrá dibujar\(n−2\) triángulos si el polígono tiene n lados.

Observe que no hemos probado la conjetura de Arthur, sino que solo encontramos varios ejemplos que son ciertos. Entonces, en este punto, decimos que la conjetura es cierta.

Ejemplo\(\PageIndex{5}\)

Dé un contraejemplo a esta afirmación: Cada número primo es un número impar.

Solución

El único contraejemplo es el número 2: un número par (no impar) que es primo.

Revisar

Dar un contraejemplo para cada una de las siguientes declaraciones.

Si\(n\) es un número entero, entonces\(n^2 >n\).
Todos los números que terminan en 1 son números primos.
Todas las fracciones positivas están entre 0 y 1.
Tres puntos cualesquiera que sean coplanarios también son colineales.
A todas las chicas les gusta el helado.
Todos los alumnos de secundaria están en coro.
Para cualquier ángulo existe un ángulo complementario.
Todos los adolescentes pueden conducir.
Si\(n\) es un número entero, entonces\(n>0\).
Todas las ecuaciones tienen soluciones enteras.

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.5.

Recursos

vocabulario

Término	Definición
conjetura	Una conjetura es una suposición educada que se basa en ejemplos en un patrón.
contraejemplo	Un contraejemplo es un ejemplo que desmiente una conjetura.
fracción	Una fracción es parte de un todo. Una fracción se escribe matemáticamente como un valor encima de otro, separado por una barra de fracción. También se le llama un número racional.

Recursos adicionales

Elemento Interactivo

Video: Razonamiento Inductivo

Actividades: Conjeturas y Contraejemplos Preguntas de discusión

Ayudas de estudio: Guía de estudio de tipos de razonamiento

Práctica: Conjeturas y Contraejemplos

Mundo real: conjeturas y contraejemplos