5.5: Frecuencia y Periodo de Funciones Sinusoidales
- Page ID
- 107477
Las reglas de transformación sobre estiramiento horizontal y contracción se aplican directamente a las gráficas de seno y coseno. Si una gráfica sinusoidal se estira horizontalmente por un factor de\(\frac{1}{2}\) eso es lo mismo que una compresión horizontal por un factor de 2.
¿Cómo cambia la ecuación cuando una gráfica de seno o coseno se estira en un factor de 3?
Periodo y Frecuencia de Funciones Sinusoidales
La ecuación general para una función sinusoidal es:
f (x) =±asin (b (x+c)) +d
El\(\pm\) controla la reflexión a través del\(x\) eje. El coeficiente\(a\) controla la amplitud. La constante\(d\) controla el desplazamiento vertical. Aquí verás que el coeficiente\(b\) controla el estiramiento horizontal.
Periodo
El estiramiento horizontal se mide para las funciones sinusoidales como sus períodos. Es por ello que a esta familia de funciones también se le llama familia de funciones periódicas. El periodo de una sinusoide es la longitud de un ciclo completo. Para las funciones básicas de seno y coseno, el periodo es\(2 \pi\). Esta longitud se puede medir de múltiples maneras. En problemas verbales y en otras circunstancias difíciles, puede ser más útil medir de pico a pico.
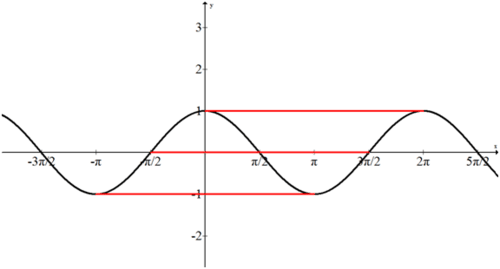
Las siguientes tres olas tienen periodos diferentes. Para clasificar cada ola por periodo de la más corta a la más larga, mira la distancia entre cada pico.
La onda roja tiene el periodo más corto.
Las ondas verdes y negras tienen periodos iguales. A pesar de que la onda verde tiene mayor amplitud que la onda negra, ambas tienen el mismo periodo.
La ola azul tiene el periodo más largo.
La capacidad de medir el periodo de una función de múltiples maneras permite que diferentes ecuaciones modele una gráfica idéntica. En la imagen de arriba, la línea roja superior representaría una onda coseno regular. La línea roja central representaría una onda sinusoidal regular con un desplazamiento horizontal. La línea roja inferior representaría una onda coseno negativa con un desplazamiento horizontal. Esta flexibilidad en perspectiva significa que muchos de los ejemplos, la práctica guiada y los problemas de práctica pueden tener múltiples soluciones. Por ahora, trata de elegir siempre la función que tenga un periodo a partir de\(x=0\).
Frecuencia
La frecuencia es una forma diferente de medir el estiramiento horizontal. Para el sonido, la frecuencia se conoce como tono. Con las funciones sinusoidales, la frecuencia es el número de ciclos que ocurren en\(2 \pi\). Un período más corto significa que pueden caber más ciclos\(2 \pi\) y, por lo tanto, una frecuencia más alta. Período y frecuencia están inversamente relacionados por la ecuación:
periodo\(=\frac{2 \pi}{\text { frequency }}\)
La ecuación de una función sinusoidal básica es\(f(x)=\sin x\). En este caso\(b\), la frecuencia, es igual a 1 lo que significa que ocurre un ciclo en\(2 \pi .\) Si\(b=\frac{1}{2},\) el periodo es\(\frac{2 \pi}{\frac{1}{2}}\) lo que significa que el periodo es\(4 \pi\) y la gráfica se estira.
Ejemplos
Anteriormente, se le preguntó cómo cambia una ecuación cuando una gráfica de seno o coseno se estira en un factor de 3. Si una gráfica sinusoidal se estira horizontalmente por un factor de 3 entonces la ecuación general tiene\(b=\frac{1}{3}\). Esto se debe a que\(b\) es la frecuencia y cuenta el número (o fracción) de un periodo que cabe en un periodo normal de\(2 \pi\). Gráficamente, la onda sinusoidal hará un ciclo completo en\(6 \pi\). De igual manera, una gráfica coseno tendrá\(b=\frac{1}{3}\) y tendrá un periodo de\(6 \pi\).
Identificar la amplitud, desplazamiento vertical, periodo y frecuencia de la siguiente función. Después grafica la función.
\(f(x)=2 \sin \left(\frac{x}{3}\right)+1\)
\(a=2, b=\frac{1}{3}, d=1\)
La amplitud es 2, el desplazamiento vertical es\(1,\) y la frecuencia es\(\frac{1}{3}\). El periodo sería\(\frac{2 \pi}{\frac{1}{3}}\), o\(6\pi\).
A menudo, la parte más desafiante de graficar funciones periódicas es etiquetar los ejes. ya que el período se\(6 \pi,\) inicia dibujando el eje sinusoidal desplazado apropiadamente. Luego divida el\(6 \pi\) en cuatro partes para que los 5 puntos de guía de la gráfica sinusoidal se puedan trazar con la amplitud y la reflexión en mente. Lo último que hay que hacer es dibujar y extender la curva.
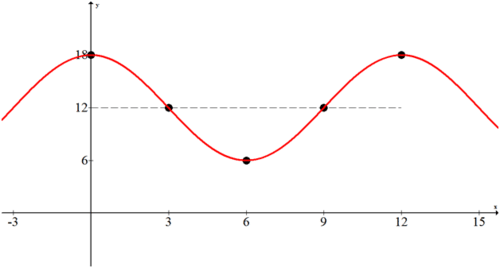
Un palo medidor en un muelle mide la marea alta para ser de 18 pies y la marea baja para ser de 6 pies. La marea tarda aproximadamente 6 horas en cambiar entre mareas bajas y altas. Determinar un modelo gráfico y algebraico para las mareas sabiendo que en\(t=0\) hay una marea alta.
Por lo general, el mejor curso de acción para los problemas verbales es identificar información, trazar puntos, bosquejar y luego finalmente llegar a una ecuación.
De la información dada se pueden deducir los siguientes puntos. Observe cómo se puede suponer que el eje sinusoidal es el promedio de las mareas alta y baja.
\ (
\ begin {array} {|l|l|}
\ hline\ text {Tiempo (horas)} &\ texto {Nivel de agua (pies)}\
\\ hline 0 & 18\
\\ hline 6 & 6\
\\ hline 12 & 18\
\ hline 3 &\ frac {18+6} {2} =12\\
\ hline 9 & 12 \
\ hline
\ end {array}
\)
Al trazar esos puntos y rellenar el eje sinusoidal se puede observar una gráfica coseno.
La amplitud es 6 así\(a=6\). No hay reflexión vertical. ya que el periodo es 12 se puede determinar la frecuencia\(b\):
\(12=\frac{2 \pi}{b} \rightarrow b=\frac{\pi}{6}\)
El desplazamiento vertical es 12 así\(d=12\). Así tienes todas las piezas para hacer un modelo algebraico:
\(f(x)=6 \cdot \cos \left(\frac{\pi}{6} x\right)+12\)
Grafique la siguiente función:\(g(x)=-\cos (8 x)+2\)
El etiquetado es la parte más importante y desafiante de este problema. La amplitud es\(1 .\) La forma es un coseno negativo. El desplazamiento vertical es\(2 .\) El periodo es\(\frac{2 \pi}{8}=\frac{\pi}{4}\)
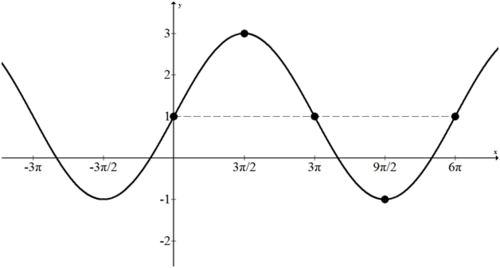
Dada la siguiente gráfica, identificar la amplitud, el período y la frecuencia y crear un modelo algebraico.
La amplitud es\(3 .\) La forma es un coseno negativo. El periodo es el\(\frac{5 \pi}{2}\) que implica eso\(b=\frac{4}{5}\). El desplazamiento vertical es 1. \(f(x)=-3 \cdot \cos \left(\frac{4}{5} x\right)+1\)
Revisar
Encuentra la frecuencia y periodo de cada función a continuación.
1. \(f(x)=\sin (4 x)+1\)
2. \(g(x)=-3 \cos (2 x)\)
3. \(h(x)=\cos \left(\frac{1}{2} x\right)+2\)
4. \(k(x)=-2 \sin \left(\frac{3}{4} x\right)+1\)
5. \(j(x)=4 \cos (3 x)-1\)
Grafica cada una de las siguientes funciones.
6. \(f(x)=3 \sin (2 x)+1\)
7. \(g(x)=2.5 \cos (\pi x)-4\)
8. \(h(x)=-\sin (4 x)-3\)
9. \(k(x)=\frac{1}{2} \cos (2 x)\)
10. \(j(x)=-2 \sin \left(\frac{3}{4} x\right)-1\)
Crear un modelo algebraico para cada una de las siguientes gráficas.
11.
12.
13.
14. A la hora 0 es marea alta y el agua en un lugar determinado es de 10 pies de altura. Con la marea baja 6 horas después, el agua mide 2 pies de altura. Dado que las mareas pueden modelarse mediante funciones sinusoidales, busque una gráfica que modele este escenario.
15. Encuentra la ecuación que modela el escenario en el problema anterior.
...