1.3.1: Límites y asíntotas

Asintotas y comportamiento final

La mayoría de las funciones continúan más allá de la ventana de visualización en nuestra calculadora o computadora. La gente suele dibujar una flecha junto a una línea punteada para indicar el patrón específicamente. ¿Cómo se pueden reconocer estas asíntotas?

---

Asintotas y Comportamiento Final de Funciones

Una asíntota vertical es una línea vertical como x=1 que indica dónde no se define una función y, sin embargo, se acerca infinitamente a.

Una asíntota horizontal es una línea horizontal como y=4 que indica dónde se aplana una función a medida que x se vuelve muy grande o muy pequeña. Una función puede tocar o pasar a través de una asíntota horizontal.

La función recíproca tiene dos asíntotas, una vertical y otra horizontal. La mayoría de las computadoras y calculadoras no dibujan las asíntotas y por lo tanto deben insertarse a mano como líneas punteadas.

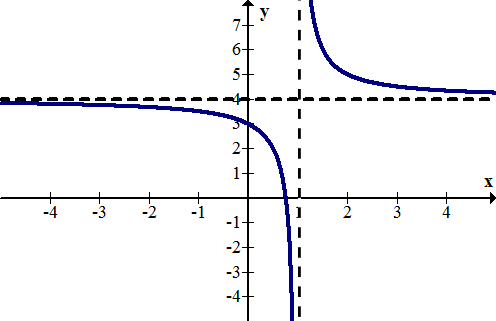[Figura1]

Muchos estudiantes tienen la idea errónea de que una asíntota es una línea a la que una función se acerca infinitamente pero no toca. Esto no es cierto. Tome la siguiente función:

[Figura2]

La gráfica parece aplanar a medida que x se hace más grande. Así, la asíntota horizontal es y=0 aunque la función pase claramente por esta línea un número infinito de veces.

La razón por la que las asíntotas son importantes es porque cuando tu perspectiva se aleja, las asíntotas se convierten esencialmente en la gráfica.

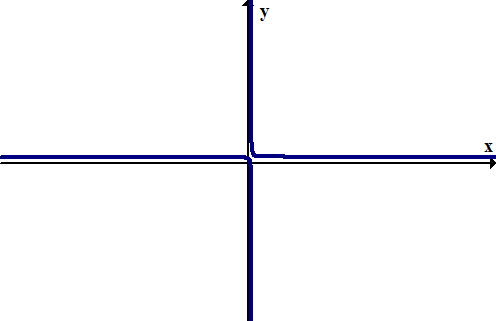[Figura3]

Para encontrar las asíntotas y el comportamiento final de la función a continuación, examine qué sucede con x e y a medida que cada uno aumenta o disminuye.

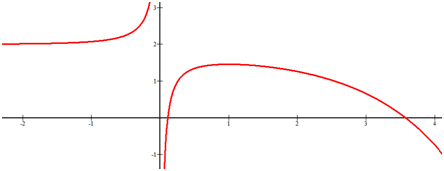[Figura4]

La función tiene una asíntota horizontal y=2 a medida que x se acerca al infinito negativo. Hay una asíntota vertical en x=0. El lado derecho parece disminuir para siempre y no tiene asíntota.

Tenga en cuenta que las asíntotas inclinadas sí existen y se llaman asíntotas oblicuas.

---

Ejemplos

Ejemplo 1

Solución

Anteriormente, se le preguntó cómo identificar asíntotas en una gráfica. Las asíntotas escritas a mano suelen identificarse con líneas punteadas junto a la función que indican cómo se comportará la función fuera de la ventana de visualización. Las ecuaciones de estas líneas punteadas verticales y horizontales son de la forma x=y y=. Cuando los problemas te piden encontrar las asíntotas de una función, están pidiendo las ecuaciones de estas líneas horizontales y verticales.

Ejemplo 2

Identificar las asíntotas horizontales y verticales de la siguiente función.

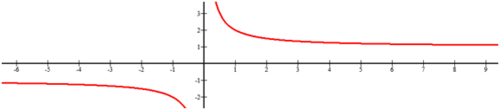[Figura5]

Solución

Hay una asíntota vertical en x=0. A medida que x se vuelve infinitamente pequeña, hay una asíntota horizontal en y=−1. A medida que x se vuelve infinitamente grande, hay otra asíntota horizontal en y=1.

Ejemplo 3

Identificar las asíntotas horizontales y verticales de la siguiente función.

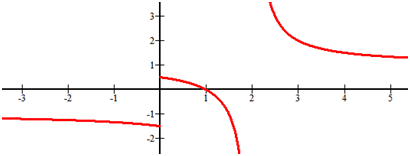[Figura6]

Solución

Hay una asíntota vertical en x=2. A medida que x se vuelve infinitamente pequeña, hay una asíntota horizontal en y=−1. A medida que x se vuelve infinitamente grande, hay una asíntota horizontal en y=1.

Ejemplo 4

Identificar las asíntotas horizontales y verticales de la siguiente función por partes:

\ (\ f (x) =\ left\ {\ begin {array} {ll}
e^ {x} -1 & x\ leq 0\\
\ sin x & 0<x
\ end {array}\ derecha.\)

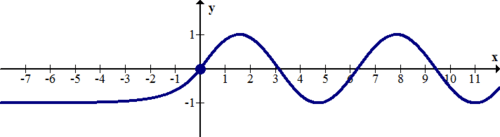[Figura7]

Solución

Hay una asíntota horizontal en y=−1 a medida que x se vuelve infinitamente pequeña. Esto se debe a que e elevado a la potencia de un número muy pequeño se convierte en 0.000000... y básicamente se convierte en cero.

Ejemplo 5

Identificar las asíntotas y el comportamiento final de la siguiente función.

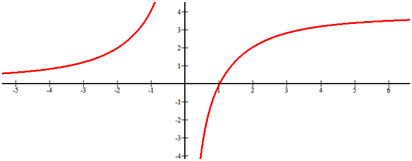[Figura8]

Solución

Hay una asíntota vertical en x=0. El comportamiento final del lado derecho e izquierdo de esta función no coincide. La asíntota horizontal cuando x se acerca al infinito negativo es y=0 y la asíntota horizontal cuando x se acerca al infinito positivo es y=4. En este punto sólo se pueden estimar estas alturas porque no se le dio la función o las herramientas para encontrar estos valores analíticamente.

---

Revisar

Identificar las asíntotas y el comportamiento final de las siguientes funciones.

1. y=x

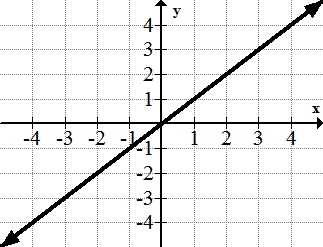[Figura9]

2. y=x ²

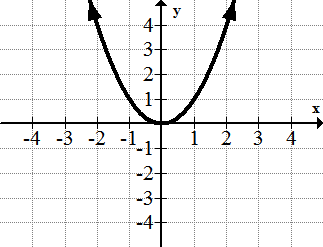[Figura10]

3. y=x ³

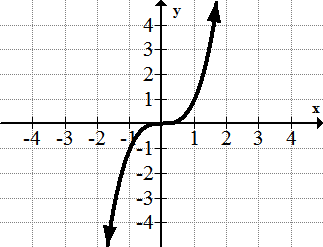[Figura11]

4. y=\(\ \sqrt{x}\)

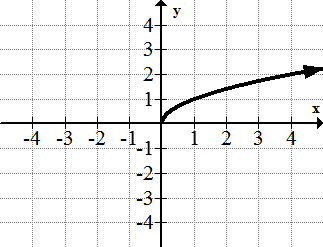[Figura12]

5. y=\(\ 1\over 2\)

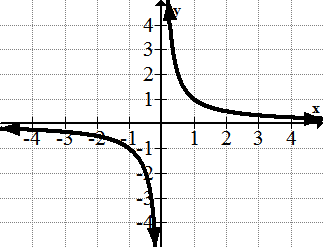[Figura13]

6. y=e ^x

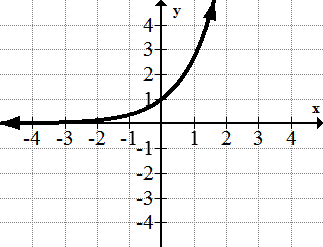[Figura14]

7. y=ln (x)

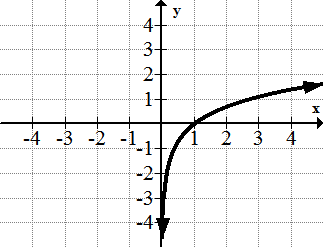[Figura15]

8. \(\ y=\frac{1}{1+e^{-x}}\)

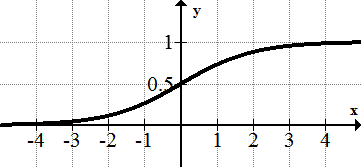[Figura16]

9.

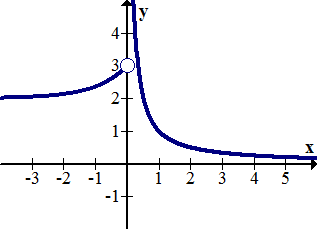[Figura17]

10.

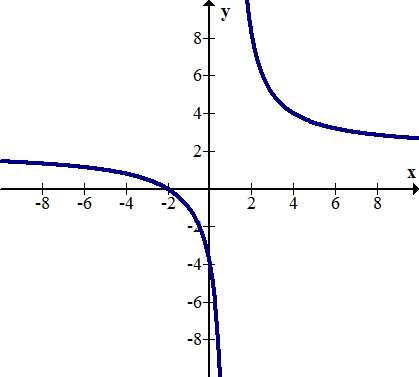[Figura18]

11.

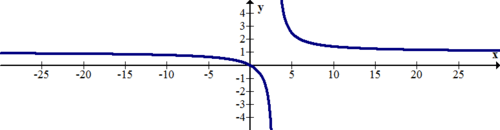[Figura19]

12. Las asíntotas verticales ocurren en valores x donde no se define una función. Explique por qué\(\ y=\frac{1}{x}\) tiene sentido que tenga una asíntota vertical en x=0.

13. Las asíntotas verticales ocurren en valores x donde no se define una función. Explica por qué tiene sentido que\(\ y=\frac{1}{x+3}\) tenga una asíntota vertical en x=−3.

14. Utilice la técnica del problema anterior para determinar la asíntota vertical para la función\(\ y=\frac{1}{x-2}\).

15. Usa la técnica del problema #13 para determinar la asíntota vertical para la función\(\ y=\frac{2}{x+4}\)

---

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.9.

---

El vocabulario

Término	Definición
Aintótico	Una función es asintótica a una línea dada si la línea dada es una asíntota de la función.
Asintota horizontal	Una asíntota horizontal es una línea horizontal que indica dónde se aplana una función ya que la variable independiente se vuelve muy grande o muy pequeña. Una función puede tocar o pasar a través de una asíntota horizontal.
Asintota oblicua	Una asíntota oblicua es una línea diagonal que marca un rango específico de valores hacia los cuales la gráfica de una función puede acercarse, pero generalmente nunca llegar. Existe una asíntota oblicua cuando el numerador de la función es exactamente un grado mayor que el denominador. Una asíntota oblicua se puede encontrar a través de una división larga.
Asintotas oblicuas	Una asíntota oblicua es una línea diagonal que marca un rango específico de valores hacia los cuales la gráfica de una función puede acercarse, pero generalmente nunca llegar. Existe una asíntota oblicua cuando el numerador de la función es exactamente un grado mayor que el denominador. Una asíntota oblicua se puede encontrar a través de una división larga.
Función por piezas	Una función por partes es una función que junta dos o más partes de otras funciones para crear una nueva función.
Asintota inclinada	Una asíntota inclinada es una línea diagonal que marca un rango específico de valores hacia los que la gráfica de una función puede acercarse, pero nunca alcanzará. Existe una asíntota inclinada cuando el numerador de la función es exactamente un grado mayor que el denominador. Una asíntota inclinada se puede encontrar a través de una división larga.
Asintota vertical	Una asíntota vertical es una línea vertical que marca un valor específico hacia el que puede acercarse la gráfica de una función, pero nunca alcanzará.

---

Atribuciones de imagen

1. [Figura 1]
   Crédito: Fundación CK-12
   Fuente: https://commons.wikimedia.org/wiki/File:Boston_Police_Special_Operations_Unit.jpg
   Licencia: CC BY-SA
2. [Figura 2]
   Crédito: Fundación CK-12
   Licencia: CC BY-SA
3. [Figura 3]
   Crédito: Fundación CK-12
   Licencia: CC BY-SA
4. [Figura 4]
   Crédito: Fundación CK-12
   Licencia: CC BY-SA
5. [Figura 5]
   Crédito: Fundación CK-12
   Fuente: https://commons.wikimedia.org/wiki/File:Boston_Police_Special_Operations_Unit.jpg
   Licencia: CC BY-SA
6. [Figura 6]
   Crédito: Fundación CK-12
   Licencia: CC BY-SA
7. [Figura 7]
   Crédito: Fundación CK-12
   Licencia: CC BY-SA
8. [Figura 8]
   Crédito: Fundación CK-12
   Licencia: CC BY-SA
9. [Figura 9]
   Crédito: Fundación CK-12
   Licencia: CC BY-SA
10. [Figura 10]
    Crédito: Fundación CK-12
    Licencia: CC BY-SA
11. [Figura 11]
    Crédito: Fundación CK-12
    Fuente: http://classconnection.s3.amazonaws.com/753/flashcards/449753/png/screen_shot_2011-09-21_at_8.07.32_pm1316650094429.png
    Licencia: CC BY-SA
12. [Figura 12]
    Crédito: Fundación CK-12
    Licencia: CC BY-SA
13. [Figura 13]
    Crédito: Fundación CK-12
    Licencia: CC BY-SA
14. [Figura 14]
    Crédito: Fundación CK-12
    Licencia: CC BY-SA
15. [Figura 15]
    Crédito: Fundación CK-12
    Licencia: CC BY-SA
16. [Figura 16]
    Crédito: Fundación CK-12; Paula Evans; Rob Young
    Fuente: https://www.flickr.com/photos/rob-young/1149735229/; https://commons.wikimedia.org/wiki/File:Will_%26_Grace_ Apartment_Building_ (1149735229) .jpg
    Licencia: CC BY-SA; CC BY-NC-SA
17. [Figura 17]
    Crédito: Fundación CK-12
    Licencia: CC BY-SA
18. [Figura 18]
    Crédito: Fundación CK-12
    Licencia: CC BY-SA
19. [Figura 19]
    Crédito: Fundación CK-12
    Licencia: CC BY-SA