1.3.2: Límites infinitos e inexistentes

Última actualización
Guardar como PDF

Page ID: 108984

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Límites infinitos e inexistentes

Has escuchado una y otra vez que es “contra las reglas” dividir por el número 0. Incluso la calculadora más básica devolverá alguna forma de “ERROR” si intentas dividir incluso el más pequeño de los números por 0.

¿Entiende realmente por qué está “contra las reglas”? ¿Qué es lo que realmente tiene de malo dividir por nada?

Límites infinitos e inexistentes

Las funciones pueden exhibir una serie de comportamientos diferentes ya que el valor de entrada se vuelve muy grande o muy pequeño.

A medida que x se acerca ∞, algunos valores de salida de funciones se acercan cada vez más a un solo número, otras se acercan a cero y otras continúan haciéndose más grandes o más pequeñas y más pequeñas sin límite.

En esta lección, exploraremos funciones del último tipo, funciones con límites infinitos, y los diferentes tipos de asíntotas que puedan tener.

Ejemplos

Ejemplo 1

Solución

Antes, se le dio una pregunta sobre dividir por cero.

Dividir por cero es “contra las reglas” porque no hay definición para la respuesta que obtendrías.

Considera lo que sucede a medida que tomas un valor dado y lo divides entre números cada vez más pequeños:

2/10 = 1/5

2/1 = 2

2/.1 = 20

2/.001 = 2,000

2/.000000001 = 2,000,000,000

A medida que dividimos por números progresivamente más pequeños, el cociente se hace cada vez más grande. También, podemos ver que en cada caso, el problema podría revertirse multiplicando el producto por el dividendo para obtener el divisor, por ejemplo: 2/.1 = 20 ==> 20 * .1 = 2.

Desafortunadamente, esto no funciona si realmente divides por 0, ¡incluso si asumes que dividir por cero resultó en infinito! No importa cuán grande sea el número que multipliques por cero, incluso infinito, nunca podrás volver a 2.

\(\ \therefore \frac{x}{0}=\text { undefined }\)

Ejemplo 2

Evaluar la función\(\ h(x)=\frac{x^{2}}{2 x-1}\)

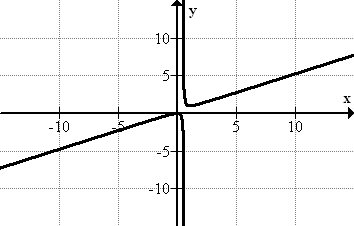
F-d_451c95076bafaf40fd3e46cb68148aac0d8ba00342263de3729e513f+image_tiny+image_tiny.jpg

Solución

Para evaluar esta función, considere el comportamiento de la función ya que se insertan valores cada vez más grandes para x. A medida que x se acerca a ∞, los valores de la función también se acercan a ∞. Por lo tanto, el límite de la función a medida que x se acerca ∞ es:\(\ \lim _{x \rightarrow \infty} \frac{x^{2}}{2 x-1}=\infty\). De manera similar, a medida que x se acerca a −∞, f (x) se acerca a −∞ Por lo tanto tenemos\(\ \lim _{x \rightarrow-\infty} \frac{x^{2}}{2 x-1}=-\infty\).

También podemos entender este límite si analizamos la ecuación para h (x). A medida que x se hace cada vez más grande, el valor de la expresión 2x - 1 se acerca cada vez más al valor de la expresión 2x. Es decir, para valores suficientemente grandes de x, 2x - 1 ≈ 2x. Por lo tanto los valores de h (x) se acercan\(\ \frac{x^{2}}{2 x}=\frac{x}{2}\).

A medida que x se hace cada vez más grande, también lo hace\(\ x\over 2\). Para valores grandes de x, la función h (x) se acerca cada vez más\(\ x\over 2\). Por lo tanto el límite es infinito.

Ejemplo 3

Aproximar la función f (x) = x ² + 2x - 3.

Solución

Esta función tiene un límite infinito a medida que x se acerca al infinito. Sin embargo, a medida que x se hace cada vez más grande, f (x) ≈ x ^², ya que el valor de x 2 crece mucho más rápido que el valor 2x, particularmente aparente a valores +/- muy grandes de x Si esto no es evidente de inmediato, evalúe la función para x = 1,000,000, ¡y obtendrá rápidamente la idea!

Por lo tanto podemos usar la función y = x ² para describir el comportamiento final de f (x).

Ejemplo 4

Describir el comportamiento final de cada gráfica. Es decir, determinar si la función tiene un límite L, si el límite es infinito, o si el límite no existe.

y=x ²
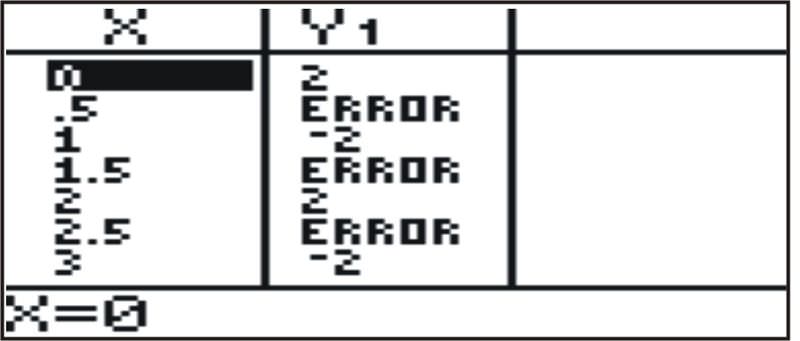
y=2 (−1) ^x
\(\ y=1-\frac{1}{|x|}\)

Solución

A medida que x se acerca a +∞, x ² también se acerca a +∞. A medida que x se acerca a −∞, x ² se acerca a +∞. Por lo tanto\(\ \lim _{x \rightarrow \infty} x^{2}=\lim _{x \rightarrow-\infty} x^{2}=\infty\).
Esta función es difícil de entender sin producir una gráfica. La tabla muestra que la función solo toma dos valores: 2 y -2, y no está definida en valores no enteros de x A medida que x se acerca a +∞ o −∞, los valores de la función alternan entre 2 y -2. Por lo tanto, el límite no existe.
Si miras la tabla de esta función, que tiene valores negativos y positivos de x, puedes ver que a medida que x se acerca a +∞ o −∞, los valores de la función se acercan a 1.

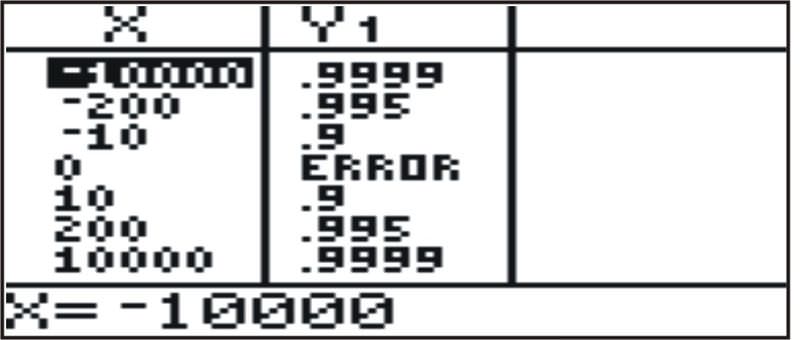
Por lo tanto\(\ \lim _{x \rightarrow \infty}\left(1-\frac{1}{|x|}\right)=\lim _{x \rightarrow-\infty}\left(1-\frac{1}{|x|}\right)=1\).
También podemos determinar este límite analíticamente. Para valores grandes de x, |x| también es grande, y también lo\(\ \frac{1}{|x|}\) es pequeño (ya que dividir 1 por un número grande da como resultado un número muy pequeño). Por lo tanto, para grandes valores de\(\ x, 1-\frac{1}{|x|} \approx 1-0=1\). Podemos hacer el mismo argumento para x acercándose a −∞.

Ejemplo 5

Evaluar\(\ \lim _{x \rightarrow \infty} \frac{x^{2}+2 x}{x-3}\).

Solución

El numerador es de mayor grado que el denominador, por lo que la función no se acerca a un límite. El denominador es x - 3, por lo que la gráfica no puede incluir 3.

Ejemplo 6

Evaluar −2x ³ −5x ² +8x.

Solución

−2x ³ −5x ² +8x es una ecuación de 3er grado, por lo que girará dos veces, ya que no es una función racional, no hay preocupaciones sobre el numerador o denominador. La función no tendrá límites, y crecerá sin ataduras tanto en la dirección positiva como en la negativa. Si utilizas una calculadora gráfica para graficar la función, verás que se puede usar y=x ³ para aproximarla.

Revisar

Para las preguntas 1-3: El límite de f (x) como x→t no puede existir si ¿qué condiciones son ciertas? Enumere tres condiciones.

Una condición es...
Una segunda condición es...
Una tercera condición es...

Dar un ejemplo de un límite que no existe

Preguntas 5-7: Suponiendo que f (x) es una función racional:

¿Qué es\(\ \lim _{x \rightarrow \infty} f(x)\) cuando el grado del numerador es menor que el grado del denominador?
¿Qué es\(\ \lim _{x \rightarrow \infty} f(x)\) cuando los grados del numerador y el denominador son iguales?
¿Qué es\(\ \lim _{x \rightarrow \infty} f(x)\) cuando el grado del numerador es mayor que el grado del denominador?
En general, si r es un número real positivo, ¿qué es\(\ \lim _{x \rightarrow \infty} \frac{1}{x^{r}}\)?
En general, si r es un número real positivo, ¿qué es\(\ \lim _{x \rightarrow \infty} x^{r}\)?

Preguntas 10-13: Que a y b sean números reales y que t sea un entero positivo. Completa cada una de las siguientes propiedades de límites.

10. \(\ \lim _{x \rightarrow a} x^{t}=\)

11. Si f es un polinomio,\(\ \lim _{x \rightarrow a} f(x)=\)

12. \(\ \lim _{x \rightarrow a} k \cdot f(x)=\)

13. \(\ \lim _{x \rightarrow \infty} t^{x}=\)

Preguntas 14-16: Evaluar.

14. \(\ \lim _{x \rightarrow-5} \frac{(5+x)^{2}-25}{x}\)

15. \(\ \lim _{x \rightarrow 3} \frac{x^{3}-6 x+2}{x^{2}+2 x-3}\)

16. \(\ \lim _{x \rightarrow 0} \frac{(3+3 y)^{-1}-3 y^{-1}}{x}\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.9.

El vocabulario

Término	Definición
∞	El símbolo “∞” significa “infinito”, y es un concepto abstracto que describe un valor mayor que cualquier número contable.
asíntotas	Una asíntota es una línea en la gráfica de una función que representa un valor hacia el que la función puede acercarse, pero no alcanza (con ciertas excepciones).
límite infinito	Una función tiene un límite infinito si su salida se acerca al infinito o al infinito negativo ya que se calculan valores muy grandes o muy pequeños para la variable de entrada (generalmente “x”).
infinito	El infinito es una cantidad sin límites que es mayor que cualquier número contable. El símbolo del infinito es ∞.
límite	Un límite es el valor que la salida de una función se acerca a medida que la entrada de la función se acerca a un valor dado.