2.6.4: Teorema del Valor Intermedio

Última actualización
Guardar como PDF

Page ID: 108665

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Teorema del Valor Intermedio

Esta lección introduce dos teoremas: El Teorema del Valor Intermedio y El Teorema de los Límites de los Ceros. A continuación se da una definición técnica, pero ¿qué significan realmente estos teoremas en 'lenguaje ordinario'?

Teorema del Valor Intermedio

El teorema del valor intermedio ofrece una manera de encontrar raíces de una función continua. Una definición informal de continuo es que una función es continua durante un cierto intervalo si no tiene roturas, saltos, asíntotas o agujeros en ese intervalo. Las funciones polinómicas son continuas para todos los números reales x Las funciones racionales a menudo no son continuas sobre el conjunto de números reales debido a asíntotas o agujeros en la gráfica, pero para intervalos sin agujeros, las funciones racionales son continuas.

Si sabemos que una función es continua a lo largo de algún intervalo [a, b], entonces podemos usar el teorema del valor intermedio:

Si f (x) es continuo en algún intervalo [a, b] y n está entre f (a) y f (b), entonces hay algo de c∈ [a, b] tal que f (c) =n.

Las siguientes gráficas destacan cómo funciona el teorema del valor intermedio. Considera la gráfica de la función\(\ f(x)=\frac{1}{4}\left(x^{3}-\frac{5 x^{2}}{2}-9 x\right)\) a continuación en el intervalo [-3, -1].

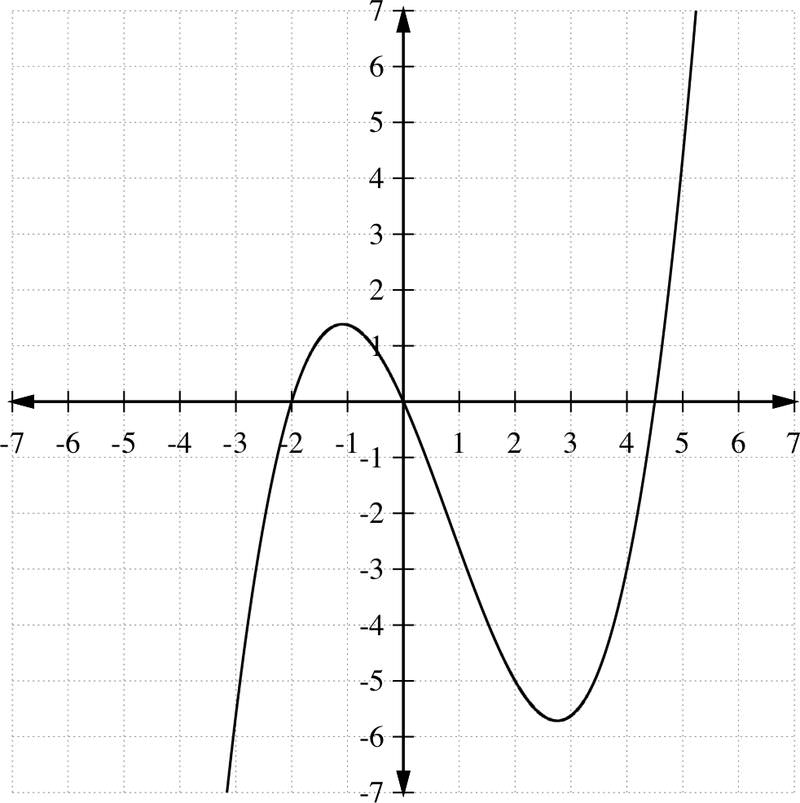
f-d_736d44b8ff22cad51de56a97d303e9897adde942bac11812cf89cbe7+image_tiny+image_tiny.jpg

f (−3) =−5.625 y f (−1) =1.375. Si dibujamos límites en [-3, -1] y [f (−3), f (−1)], entonces vemos que para cualquier valor y−entre y=−5.625 e y=1.375, debe haber un valor x en [-3, -1] tal que f (x) =y.

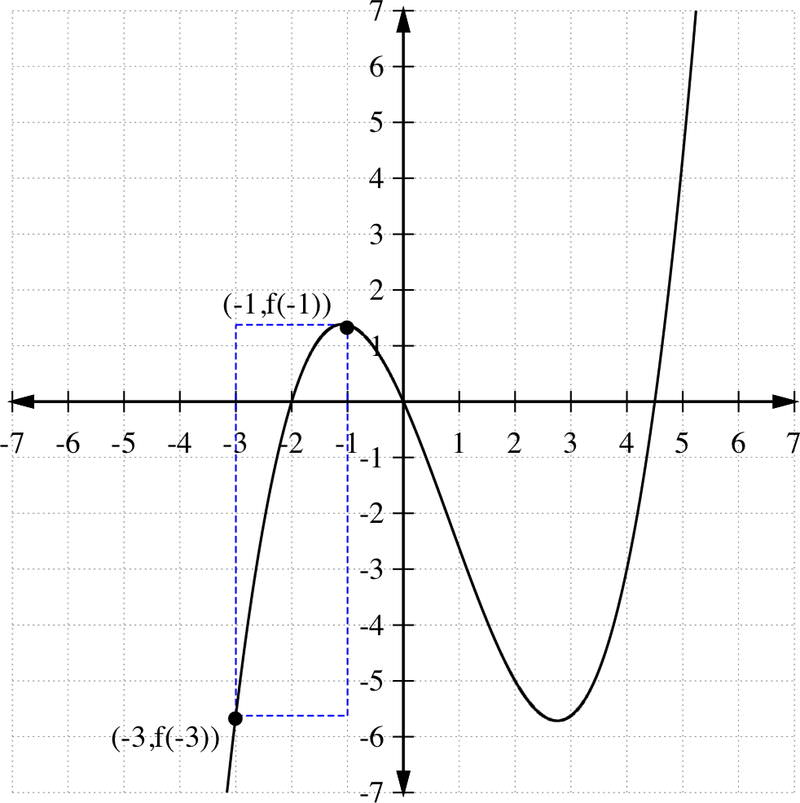
F-d_81cf58cc0cbf1c932f2019c9f9915a5451b34ee35098ecf9ce59615b+image_tiny+image_tiny.jpg

Entonces, por ejemplo, si elegimos c=−2, sabemos que para algunos x ∈ [−3, −1], f (x) =−2, ¡aunque resolver esto a mano sería una tarea!

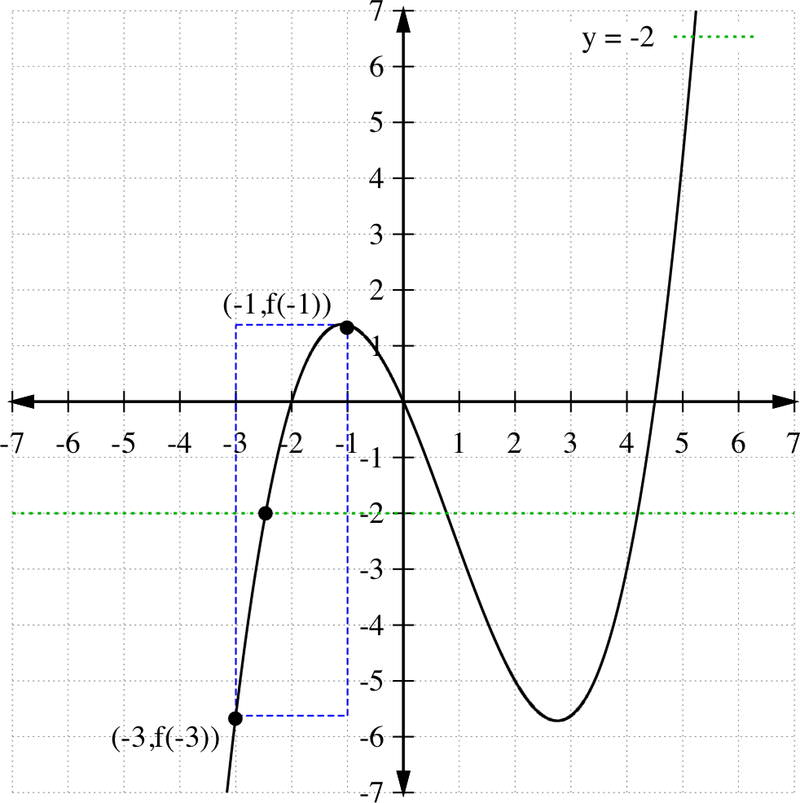
F-d_a46bb5fc02645d28d70d1fa4c4d3d75a8ce9fde854749cefc53d3f35+image_tiny+image_tiny.jpg

Los límites en el teorema de ceros es un corolario del Teorema del Valor Intermedio:

Los límites en el teorema de ceros

Si f es continuo en [a, b] y hay un cambio de signo entre f (a) y f (b) (es decir, f (a) es positivo y f (b) es negativo, o viceversa), entonces hay un c∈ (a, b) tal que f (c) =0.

Los límites en el teorema de ceros es un corolario del teorema del valor intermedio porque no es fundamentalmente diferente de la declaración general del teorema del valor intermedio, solo un caso especial donde n=0.

Mirando hacia atrás en\(\ f(x)=\frac{1}{4}\left(x^{3}-\frac{5 x^{2}}{2}-9 x\right)\) lo anterior, porque f (−3 <0 and f (−1) > ≈0, sabemos que para algunos x∈ [−3, −1], f (x) tiene una raíz. De hecho, esa raíz está en x=−2. y podemos probarla usando división sintética o evaluando f (−2) directamente.

Ceros aproximados de funciones polinómicas

En cálculo aprenderás varios métodos para aproximar numéricamente las raíces de las funciones. En esta sección mostramos un método numérico elemental para encontrar los ceros de un polinomio que aprovecha el Teorema del Valor Intermedio.

Dada una función continua g (x),

Encuentra dos puntos de tal manera que g (a) > 0 y g (b) < 0. Una vez que hayas encontrado estos dos puntos, puedes usar iterativamente los pasos a continuación para encontrar la raíz de g (x) en el intervalo [a, b]. (Nota, asumiremos a < b, but the same algorithm works with minor adjustments if b > a)
Evaluar\(\ g\left(\frac{a+b}{2}\right)\).
1. Si\(\ g\left(\frac{a+b}{2}\right)=0\), entonces la raíz es\(\ x=\frac{a+b}{2}\).
2. Si\(\ g\left(\frac{a+b}{2}\right)>0\), reemplace a con\(\ \frac{a+b}{2}\). y repita los pasos 1-2 usando\(\ \left[\frac{a+b}{2}, b\right]\)
3. Si\(\ g\left(\frac{a+b}{2}\right)<0\), reemplace b por\(\ \frac{a+b}{2}\). y repita los pasos 1-2 usando\(\ \left[a, \frac{a+b}{2}\right]\)

Este algoritmo no suele encontrar la raíz exacta de g (x), pero te permitirá encontrar un intervalo razonablemente pequeño para la raíz. Por ejemplo, podrías repetir este proceso suficientes veces para que encuentres un intervalo con |a−b|<0.01, y conocerás la raíz de g (x) dentro de una aproximación razonablemente buena. La calidad de la aproximación que utilices (y el número de pasos que utilices) dependerá de por qué estés buscando la raíz. Para la mayoría de las aplicaciones que se encuentran dentro de 0.01 de la raíz es una aproximación razonable, pero para algunas aplicaciones (como construir un puente o lanzar un cohete) se necesita mucha más precisión.

Un Corolario Interesante del Teorema del Valor Intermedio

Un resultado sorprendente del Teorema del Valor Intermedio es que si dibujas algún gran círculo alrededor del globo, entonces deben haber dos puntos antípodas en ese gran círculo que tengan exactamente la misma temperatura.

Recordemos que un gran círculo es un camino alrededor de una esfera que da la distancia más corta entre dos puntos cualesquiera de la esfera. El ecuador es un gran círculo alrededor del globo. Los puntos antípodas son dos puntos en lados opuestos de la esfera. En el diagrama siguiente, B y B′ son antípodas.

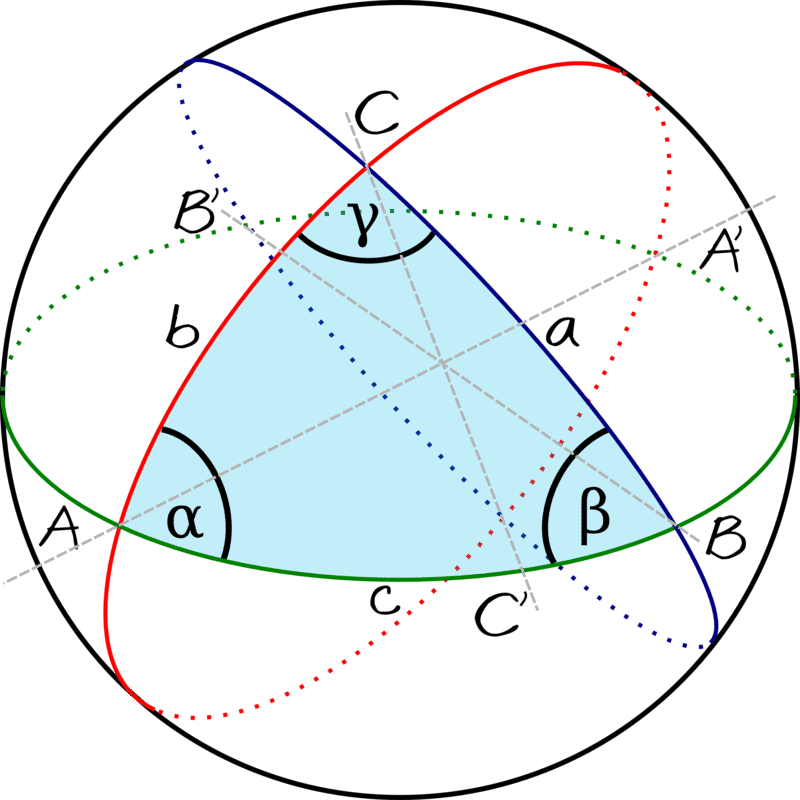
f-d_8df0caeed21dff4015df8d9c16b76bb986c3dd1689bf8544e60afa83+image_tiny+image_tiny.png

Para una prueba informal de este resultado, mira la imagen de una esfera con tres grandes círculos arriba. Supongamos que la temperatura en B es 75° y la temperatura B′ es 50°. La diferencia entre la temperatura a B y a B′ es 75−50=25. Ahora imagina rotar el segmento\(\ \overline{B B^{\prime}}\) alrededor del gran círculo azul. Cuando el segmento ha girado 180 grados (es decir, cuando B ha girado hasta donde B′ está), entonces la diferencia entre las temperaturas en estos dos puntos es 50−75=−25. Dado que las temperaturas varían continuamente, según el teorema del valor intermedio, debe haber algún punto en ese círculo cuando la diferencia fue 0, lo que implica que dos puntos antípodas tenían la misma temperatura.

Observe que esta pequeña demostración no nos dice cuáles dos puntos antípodas tenían la misma temperatura, solo que debe haber dos puntos de este tipo en cualquier gran círculo.

Ejemplos

Ejemplo 1

Anteriormente, se le preguntó si podría escribir definiciones menos formales del Teorema del Valor Intermedio y del Teorema de Límites sobre los Ceros.

Solución

Una posibilidad podría ser:

El Teorema del Valor Intermedio simplemente establece que si conoces dos puntos en una gráfica, y sabes que la gráfica incluye todos los puntos entre ellos, entonces cualquier punto entre ellos debe estar en la gráfica.

El teorema de límites en ceros sugiere que si una gráfica contiene todos los puntos entre un valor positivo y uno negativo, entonces un punto cero entre esos dos valores está en la gráfica.

Ejemplo 2

Mostrar que f (x) =−3x ³ +5x tiene al menos una raíz en el intervalo [1, 2].

Solución

Dado que f (x) es un polinomio sabemos que es continuo. f (1) = 2 y f (2) = −14. Dejar n = 0 ∈ [−14,2]. Aplicando el Teorema del Valor Intermedio, debe existir algún punto c ∈ [1,2] tal que f (c) = 0. Esto demuestra que f (x) tiene una raíz en [1, 2].

Ejemplo 3

La siguiente tabla muestra varios valores muestrales de un polinomio p (x).

x	−4	−2	0	1	4	6	8	10	15	18
p (x)	44.15	6.62	−4.12	−4.09	1.16	0	−8.74	−24.07	−49.8918	3.41

Solución

Con base en la información de la tabla:

a. ¿Cuál es el número mínimo de raíces de p (x)?

b. ¿Cuáles son los límites en las raíces de p (x) que identificó en (a)?

Dado que p (x) es un polinomio ya sabemos que es continuo. Podemos usar el Teorema del Valor Intermedio para identificar raíces observando cuándo p (x) cambia de negativo a positivo, o de positivo a negativo.

a. hay cuatro cambios de signo de p (x) en la tabla, por lo que como mínimo, p (x) tiene cuatro raíces.

b. Las raíces están en los siguientes intervalos x ∈ [−2, 0], x ∈ [1, 4], x ∈ [15, 18], y la tabla también nos dice que una raíz está en x=6.

Ejemplo 4

Muestra las primeras 5 iteraciones de encontrar la raíz de h (x) =x ² −x−1 usando los valores iniciales a=0 y b=2.

Solución

Primero verificamos que hay una raíz entre x=0 y x=2. h (0) =−1 y h (2) =1 así sabemos que hay una raíz en el intervalo [0, 2]. Cheque\(\ h\left(\frac{2+0}{2}\right)=h(1)=-1\). Desde −1 < 0 sabemos que la raíz está entre x=1 y x=2, y usamos el nuevo intervalo [1, 2].
Ahora usamos el intervalo [1, 2]. \(\ h\left(\frac{1+2}{2}\right)=h(1.5)=-0.25\). Desde −0.25 < 0, usamos el intervalo [1.5, 2].
\(\ h\left(\frac{1.5+2}{2}\right)=h(1.75)=0.31\). Desde 0.31 > 0, sabemos que el cero está en el intervalo [1.5, 1.75].
\(\ h\left(\frac{1.5+1.75}{2}\right)=h(1.625)=0.02\). Desde 0.02 > 0, sabemos que la raíz está entre 1.5 y 1.625.
\(\ h\left(\frac{1.5+1.625}{2}\right)=h(1.5620)=-0.12\). Desde −0.12 < 0, sabemos que la raíz está entre 1.5620 y 1.625.

Este ejemplo muestra que después de cinco iteraciones hemos reducido la posible ubicación de la raíz a 0.06 unidades. ¡No está mal!

Ejemplo 5

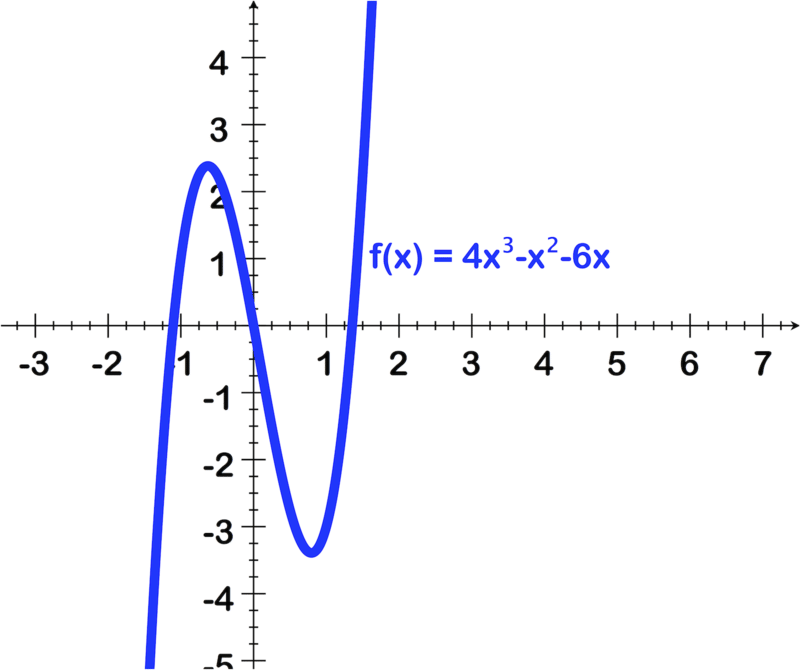
Utilice la imagen de la gráfica a continuación para encontrar lo siguiente:

Grado del polinomio
Número de ceros reales y sus valores aproximados usando la gráfica
Número de ceros imaginarios

F-D_c1333772de1712d3725320f391e134f829080d2cf94c3e6182a1cec0+image_tiny+image_tiny.png

Solución

Para identificar el grado, recordemos que el grado de un polinomio es un número mayor que el número de giros. La imagen muestra giros a apx x = -.6 y apx x = .75, por lo tanto esta es una función de 3er grado.
La imagen muestra la línea que cruza el eje x 3 veces, a (apx) -1.15, a 0 y a (apx) 1.4.
Al tratarse de una ecuación de 3er grado hay 3 ceros posibles, y como hay 3 ceros reales no hay imaginarios.

Ejemplo 6

Mostrar que f (x) =8x ³ −5x ² −7x−5 tiene al menos una raíz en el intervalo [1, 2].

Solución

Dado que f (x) es un polinomio sabemos que es continuo. f (1) = −9 y f (2) = 25. Dejar n = 0 ∈ [−9, 25]. Aplicando el Teorema del Valor Intermedio, debe existir algún punto c ∈ [1,2] tal que f (c) = 0. Esto demuestra que f (x) tiene una raíz en [1, 2].

Tenga en cuenta que como se trata de un polinomio de 3er grado, hay tres ceros. Como sólo hay un cero real, los otros dos deben ser imaginarios.

Revisar

Para las preguntas 1 a 6, utilice la imagen de la gráfica para encontrar lo siguiente:

Coeficiente principal y grado del polinomio
Número de ceros reales y sus valores aproximados usando la gráfica
Número de ceros imaginarios

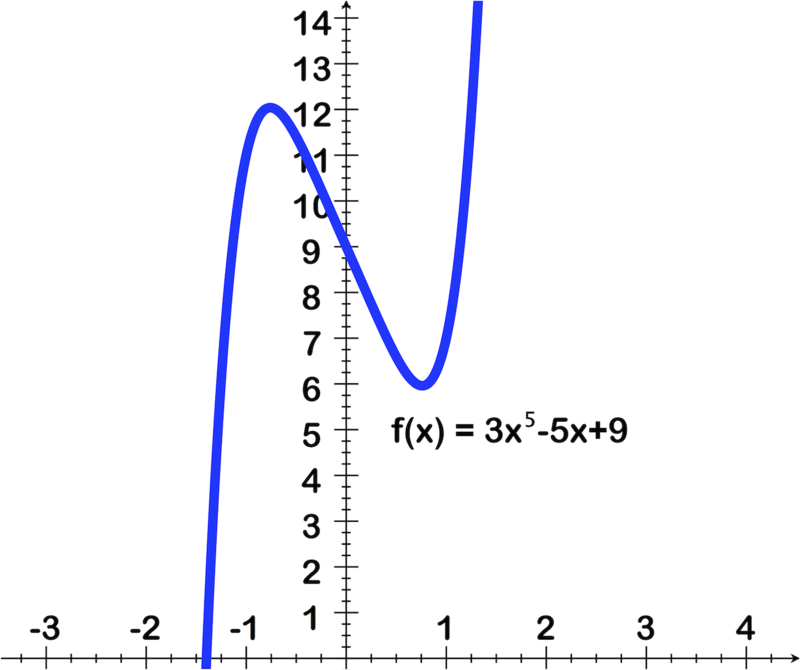F-D_dad9a8da24c1d93e91ef8f7b5009528383884457bb0add0e63af476d+image_tiny+image_tiny.png

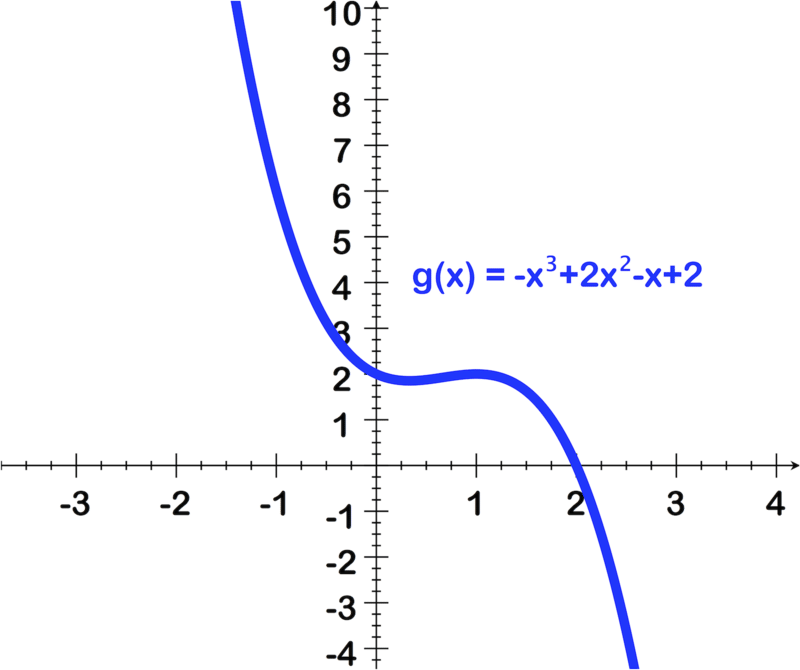f-d_47abbe70854f14709b60bae02acfd5ee8c585f930dacf7d0e0f754e1+image_tiny+image_tiny.png

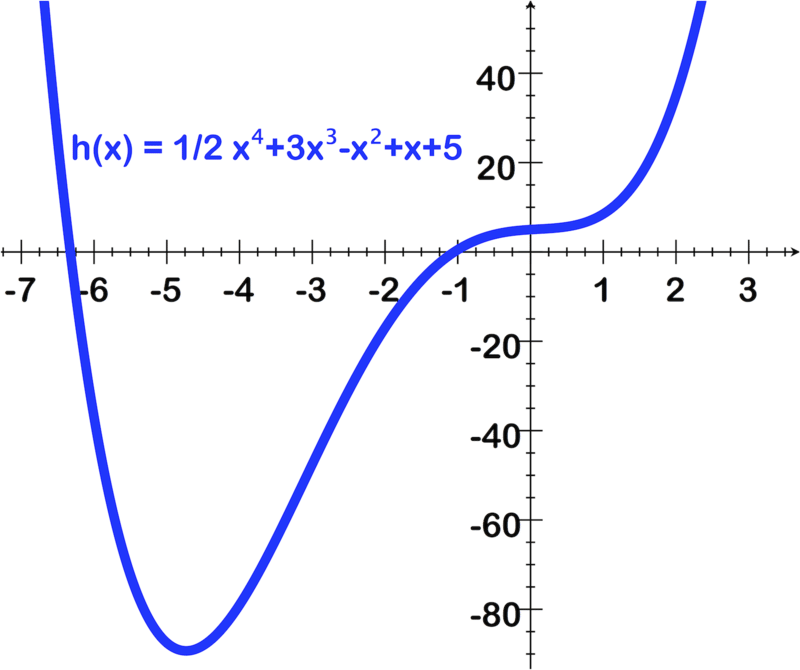F-D_60b457da519dac06164db8c51d0336fb135af816d046400f69901695+image_tiny+image_tiny.png

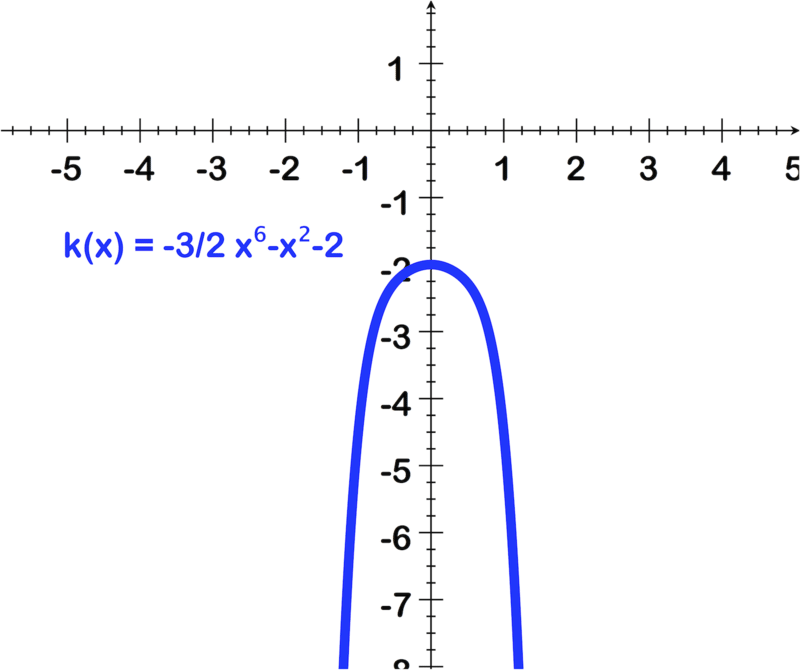
f-d_7ffd5a9aceb22cf82f63798dad60b5cdd9b3136f1c0b281479182136+imagen_tiny+imagen_tiny.png

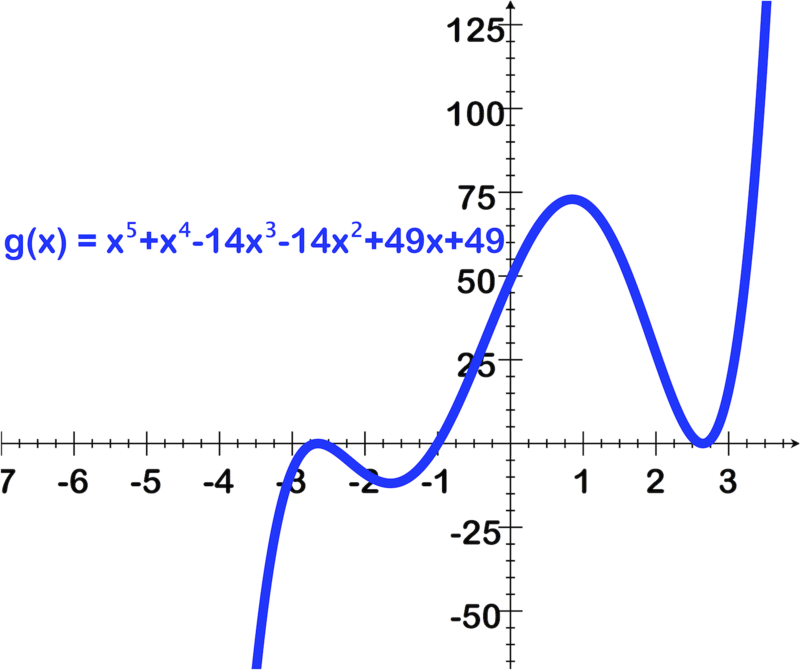f-d_6631fe69444b6a4a349e6758a912d55936624cd2ee6b1e3dfb7f9d9e+image_tiny+image_tiny.png

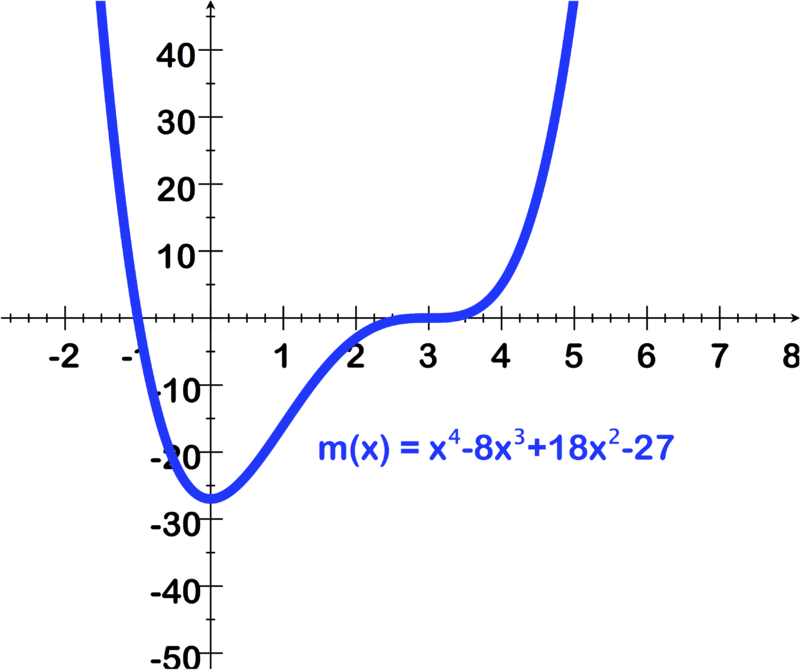f-d_27ee264fbe3632a65e672e04c3f419aa60d9068983554ed5d6302ace+image_tiny+image_tiny.png

Para las preguntas 7-12, utilice el teorema del valor intermedio para mostrar los límites en los ceros de cada función. (Tus límites deben estar dentro del número entero)

f (x) =2x ³ −3x+4
g (x) =−5x ² +8x+12
\(\ h(x)=\frac{1}{2} x^{4}-x^{3}-3 x^{2}+1\)
\(\ j(x)=-\frac{2}{x^{2}+1}+\frac{1}{2}\)

k (x) es un polinomio y los valores seleccionados de k (x) se dan en la siguiente tabla:

x	-3	-2	-1	0	1	2	3
k (x)	−23.5	−1	0.5	−1	.5	−1	−23.5

Stephen argumenta que la función\(\ r(x)=\frac{4 x+1}{x+3.5}\) tiene dos ceros basados en la siguiente tabla y una aplicación del Teorema de Límites en Ceros. ¿Qué tiene de defectuoso el razonamiento de Stephen?

x	−5	−4	−3	−2	−1	0	1	2	3	4
r (x)	12.67	30	−22	−4.67	-1.20	0.29	1.11	1.64	2.0	2.27

Para las preguntas 13-15, aplicar el algoritmo numérico cinco veces para encontrar un límite sobre los ceros de las siguientes funciones dados los valores iniciales indicados. Dar una estimación final para el cero.

k (x) =x ⁴ −3x+1 en [0,1]
b (x) =−0.1x ⁵ +3x ³ −5x ² en [1,3]
\(\ c(x)=\frac{3 x^{2}-2}{x^{4}+2} \text { on }[0,2]\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.13.

El vocabulario

Término	Definición
Líderes en el teorema de ceros	El teorema de los límites sobre ceros establece que si f es continuo en [a, b] y hay un cambio de signo entre f (a) y f (b) (es decir, f (a) es positivo y f (b) es negativo, o viceversa), entonces hay un c ∈ (a, b) tal que f (c) = 0.
Continuo	La continuidad para un punto existe cuando los límites de los lados izquierdo y derecho coinciden con la función evaluada en ese punto. Para que una función sea continua, la función debe ser continua en cada punto de un dominio ininterrumpido.
Función continua	Una función continua es una función sin roturas ni huecos. Contiene un número infinito e incontable de valores.
Teorema del valor intermedio	El teorema del valor intermedio establece que si f (x) es continuo en algún intervalo [a, b] y n está entre f (a) y f (b), entonces hay algo de c ∈ [a, b] tal que f (c) = n.
intervalo	Un intervalo es una parte específica y limitada de una función.
Función Racional	Una función racional es cualquier función que pueda escribirse como la relación de dos funciones polinómicas.
División Sintética	La división sintética es una versión abreviada de la división polinómica larga donde solo se utilizan los coeficientes del polinomio.
teorema	Un teorema es una afirmación que puede demostrarse verdadera usando postulados, definiciones y otros teoremas que ya han sido probados.
Ceros	Los ceros de una función f (x) son los valores de x que hacen que f (x) sea igual a cero.
Ceros	Los ceros de una función f (x) son los valores de x que hacen que f (x) sea igual a cero.

Atribuciones de imagen

[Figura 1]
Crédito: CK-12
Fuente: CK-12
[Figura 2]
Crédito: CK-12
Fuente: CK-12
[Figura 3]
Crédito: CK-12
Fuente: CK-12
[Figura 4]
Crédito: CK-12
Fuente: CK-12
[Figura 5]
Crédito: CK-12
Fuente: CK-12