5.2.4: Proyección vectorial
- Page ID
- 108954
Proyección vectorial
Proyectar un vector sobre otro responde explícitamente a la pregunta: “¿cuánto de un vector va en dirección al otro vector?” El producto punto es útil porque produce una cantidad escalar que ayuda a responder a esta pregunta. En este concepto, producirás un vector real no solo un escalar.
¿Por qué es útil la proyección vectorial cuando se considera tirar de una caja en la dirección de en\(\ v\) lugar de horizontalmente en la dirección de\(\ u\)?
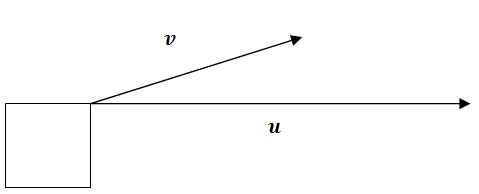
Proyecciones
Considera la pregunta desde arriba.
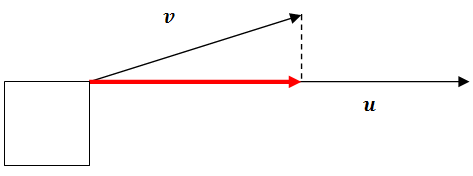
La definición de proyección vectorial para el vector rojo indicado es la llamada\(\ \operatorname{proj}_{u} v\). Cuando\(\ \operatorname{proj}_{u} v\) lees debes decir “la proyección vectorial de\(\ v\) onto”\( u\). Esto implica que el nuevo vector va en la dirección de\(\ u\). La proyección vectorial es el vector producido cuando un vector se resuelve en dos vectores componentes, uno que es paralelo al segundo vector y otro que es perpendicular al segundo vector. El vector paralelo es la proyección vectorial.
Conceptualmente, esto significa que si alguien estuviera tirando de la caja en un ángulo y fuerza de vector\(\ v\) entonces parte de su energía se desperdiciaría tirando de la caja hacia arriba y parte de la energía contribuiría realmente a tirar de la caja horizontalmente.
La definición de proyección escalar es simplemente la longitud de la proyección vectorial. Cuando la proyección escalar es positiva significa que el ángulo entre los dos vectores es menor a 90°. Cuando la proyección escalar es negativa significa que los dos vectores se dirigen en direcciones opuestas.
La fórmula de proyección vectorial se puede escribir de dos maneras. La versión de la izquierda es la más simplificada, pero la versión de la derecha tiene más sentido conceptualmente. A.
\(\ \operatorname{proj}_{u} v=\left(\frac{v \cdot u}{|u|^{2}}\right) u=\left(\frac{v \cdot u}{|u|}\right) \frac{u}{|u|}\)
La prueba de la fórmula de proyección vectorial es la siguiente:
Dados dos vectores\(\ u\),\(\ v\), ¿qué es\(\ \operatorname{proj}_{u} v\)?
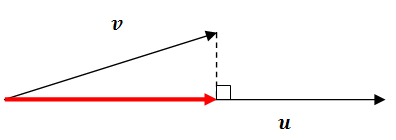
Primero tenga en cuenta que el vector proyectado en rojo irá en la dirección de\(\ u\). Esto significa que será un producto del vector unitario\(\ \frac{u}{|u|}\) y la longitud del vector rojo (la proyección escalar). Para encontrar la proyección escalar, anote el triángulo rectángulo, el ángulo desconocido θ entre los dos vectores y la relación coseno.
\(\ \cos \theta=\frac{\text { scalar projection }}{|v|}\)
Recordemos eso\(\ \cos \theta=\frac{u \cdot v}{|u||v|}\). Ahora solo sustituya y simplifique para encontrar la longitud de la proyección escalar.
\ (\\ begin {alineado}
\ cos\ theta &=\ frac {\ text {proyección escalar}} {|v|}\
\ frac {u\ cdot v} {|u||v|} &=\ frac {\ texto {proyección escalar}} {|v|}\
\ frac {u\ cdot v} {|u|} &=\ texto {proyección}
\ end {alineado}\)
Ahora tienes la longitud de la proyección vectorial y la dirección que quieres que vaya:
\(\ \operatorname{proj}_{u} v=\left(\frac{u \cdot v}{|u|}\right) \frac{u}{|u|}\)
Ejemplos
Anteriormente, se le preguntó por qué la proyección vectorial es útil al considerar tirar de una caja en la dirección de en lugar de horizontalmente en la dirección de\(\ u\). La proyección vectorial es útil en aplicaciones físicas que involucran fuerza y trabajo.
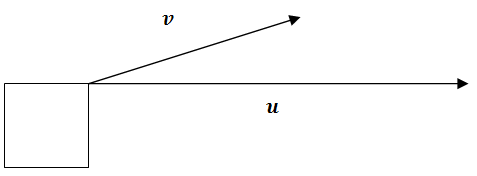
Solución
Cuando la caja es tirada por vector\(\ v\) parte de la fuerza se desperdicia tirando hacia arriba contra la gravedad. En la vida real esto puede ser útil por la fricción, pero por ahora esta energía se desperdicia ineficientemente en el movimiento horizontal de la caja.
Encuentra la proyección escalar de vector\(\ v=<3,4>\) sobre vector\(\ u=<5,-12>\).
Solución
Como se señaló anteriormente, la proyección escalar es la magnitud de la proyección vectorial. Se demostró que esto era\(\ \left(\frac{u \cdot v}{|u|}\right)\) donde\(\ u\) se proyecta el vector.
\(\ \frac{u \cdot v}{|u|}=\frac{<5,-12>\cdot<3,4>}{13}=\frac{15-48}{13}=-\frac{33}{13}\)
Encuentra la proyección vectorial de vector\(\ v=<3,4>\) sobre vector\(\ u=<5,-12>\)
Solución
Dado que la proyección escalar ya se ha encontrado en el Ejemplo 2, se debe multiplicar el escalar por el vector unitario “onto”.
\(\ -\frac{33}{13}<\frac{5}{13},-\frac{12}{13}>=<-\frac{165}{169}, \frac{396}{169}>\)
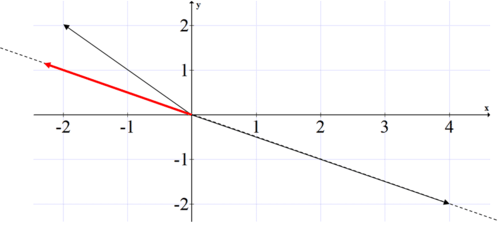
Esbozar el vector\(\ <-2,-2>\) y\(\ <4,-2>\). Explique usando un boceto por qué tiene\(\ <4,-2>\) sentido una proyección escalar negativa de\(\ <-2,-2>\) onto.
Solución
Primero grafica los dos vectores y extiende el vector “onto”. Cuando se produce la proyección del vector, el vector\(\ <-2,2>\) va en la dirección opuesta al vector\(\ <4,-2>\). Esto creará una proyección vectorial que va en la dirección opuesta a\(\ <4,-2>\).
Un padre está tirando a su hija por una colina. El cerro tiene una pendiente de 20 o. La hija está en un trineo que se sienta en el suelo y tiene una cuerda que el padre tira con una fuerza de 100 lb mientras camina. La cuerda hace un ángulo de 39 o con la pendiente. ¿Cuál es la fuerza efectiva que ejerce el padre moviendo a su hija y al trineo por la colina?
Solución
La caja representa a la niña y al trineo. La flecha azul indica la fuerza de 100 lb del padre. Observe que la pregunta pide simplemente la cantidad de fuerza que significa proyección escalar. Dado que esto no depende de la pendiente de este cerro, podemos rotar nuestra perspectiva y aún así obtener la misma proyección escalar.
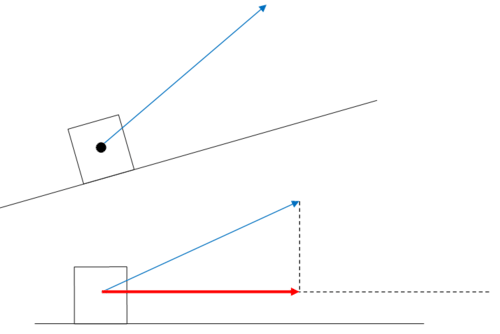
Los componentes del vector de fuerza del padre son\(\ 100<\cos 39^{\circ}, \sin 39^{\circ}>\) y el vector “onto” es cualquier vector horizontalmente a la derecha. Como solo estamos buscando la longitud del componente horizontal y ya tienes el ángulo entre los dos vectores, la proyección escalar es:
\(\ 100 \cdot \cos 39^{\circ} \approx 77.1 \mathrm{lb}\)
Revisar
- Sketch vectores\(\ <2,4>\) y\(\ <2,1>\).
- ¿Cuál es la proyección vectorial\(\ <2,4>\) sobre\(\ <2,1>\)? Esbozar la proyección.
- Sketch vectores\(\ <-2,1>\) y\(\ <-1,3>\).
- ¿Cuál es la proyección vectorial\(\ <-1,3>\) sobre\(\ <-2,1>\)? Esbozar la proyección.
- Sketch vectores\(\ <6,2>\) y\(\ <8,1>\).
- ¿Cuál es la proyección vectorial\(\ <6,2>\) sobre\(\ <8,1>\)? Esbozar la proyección.
- Sketch vectores\(\ <1,7>\) y\(\ <6,3>\).
- ¿Cuál es la proyección vectorial\(\ <1,7>\) sobre\(\ <6,3>\)? Esbozar la proyección.
- Una caja está al costado de una colina inclinada a los 30 o. El peso de la caja es de 40 libras. ¿Cuál es la magnitud de la fuerza requerida para evitar que la caja se deslice por la colina?
- Sarah está en un trineo al costado de una colina inclinada a los 60 o. El peso de Sarah y el trineo es de 125 libras. Cuál es la magnitud de la fuerza requerida para que Sam impida que Sarah se deslice cuesta abajo.
- Un auto de 1780 libras está estacionado en una calle que hace un ángulo de 15 o con la horizontal. Encuentra la magnitud de la fuerza requerida para evitar que el auto ruede cuesta abajo.
- Un auto de 1900 libras está estacionado en una calle que hace un ángulo de 10 o con la horizontal. Encuentra la magnitud de la fuerza requerida para evitar que el auto ruede cuesta abajo.
- Una fuerza de 30 libras que hace un ángulo de 32 o con un plano inclinado es jalar una caja hacia arriba del plano. El plano inclinado hace un ángulo de 20 o con la horizontal. ¿Cuál es la magnitud de la fuerza efectiva que tira de la caja por el avión?
- Una fuerza de 22 libras que hace un ángulo de 12 o con un plano inclinado es jalar una caja hacia arriba del plano. El plano inclinado hace un ángulo de 25 o con la horizontal. ¿Cuál es la magnitud de la fuerza efectiva que tira de la caja por el avión?
- Anne tira de un vagón sobre una superficie horizontal con una fuerza de 50 libras. El asa del vagón hace un ángulo de 30 o con el suelo. ¿Cuál es la magnitud de la fuerza efectiva que tira del vagón?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.5.
El vocabulario
| Término | Definición |
|---|---|
| proyección escalar | La proyección escalar de un vector sobre otro vector es igual a la longitud de la proyección del primer vector sobre el segundo vector. |
| vector de unidad | Un vector unitario es un vector con una magnitud de uno. |
| proyección vectorial | La proyección vectorial de un vector en una dirección dada es un vector con una magnitud igual a la proyección escalar. La dirección de la proyección vectorial es la misma que la del vector unitario de esa dirección dada. |
Atribuciones de imagen
- [Figura 1]
Crédito: Fundación CK-12
Fuente: https://commons.wikimedia.org/wiki/File:Prototype_Pontiac_race_car.jpg
Licencia: CC BY-SA

