5.2.3: Productos cruzados
- Page ID
- 108941
Productos cruzados
Los productos cruzados están relacionados con los productos de punto de varias maneras. Ambos son cálculos vectoriales, ambos están relacionados no sólo con la magnitud de cada vector, sino también con las direcciones relativas de ambos vectores.
Los productos de punto en cierto sentido calculan la fuerza unida de dos vectores en una dirección dada, y así son mayores cuando los vectores son paralelos. Los productos cruzados, sin embargo, son mayores cuando los vectores son perpendiculares... ¿qué calculan entonces?
Productos cruzados
Mientras que un producto de punto de dos vectores produce un valor escalar; el producto cruzado de los mismos dos vectores produce una cantidad de vector que tiene una dirección perpendicular a los dos vectores originales.
El producto cruzado de dos cantidades vectoriales es otro vector cuya magnitud varía a medida que cambia el ángulo entre los dos vectores originales. El producto cruzado a veces se conoce como el producto vectorial de dos vectores. La magnitud del producto cruzado representa el área del paralelogramo cuyos lados están definidos por los dos vectores, como se muestra en la siguiente figura. Por lo tanto, el valor máximo para el producto cruzado ocurre cuando los dos vectores son perpendiculares entre sí, pero cuando los dos vectores son paralelos entre sí la magnitud del producto cruzado es igual a cero.
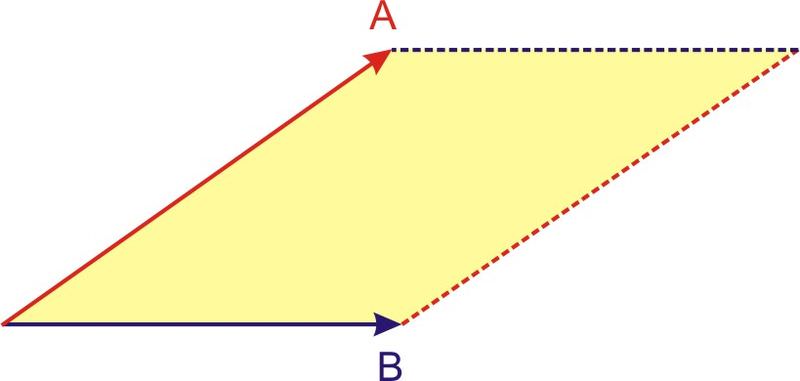
La forma algebraica de la ecuación del producto cruzado es más complicada que la del producto punto. Para dos vectores 3D\(\ \vec{A}\)\(\ \vec{B}\) y
\(\ \vec{A} \times \vec{B}=\left\langle\left(A_{2} B_{3}-A_{3} B_{2}\right),\left(A_{3} B_{1}-A_{1} B_{3}\right),\left(A_{1} B_{2}-A_{2} B_{1}\right)\right\rangle\)
Otra forma de describir el proceso es decir que el producto cruzado es la multiplicación de un vector por el componente del otro vector que es perpendicular al primer vector. En el diagrama a continuación se encuentran dos vectores, A y B. Se ha dibujado una línea perpendicular radialmente hacia afuera de B hacia A para crear un triángulo rectángulo con A como hipotenusa.
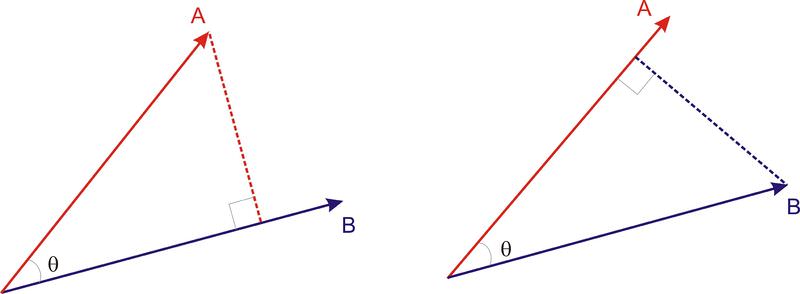
El componente del\(\ \vec{A}\) cual es perpendicular a\(\ \vec{B}\) viene dado por A sin θ por lo que la magnitud del producto cruzado se puede escribir como\(\ |\vec{A} \times \vec{B}|=\vec{A}(\vec{B} \sin \theta)=|\vec{A}||\vec{B}| \sin \theta\)
La dirección del producto transversal es perpendicular al plano definido por los dos vectores cruzados. Por ejemplo, el producto cruzado de dos vectores en el plano x-y será paralelo al eje z. Esto todavía deja dos posibles direcciones para el producto cruzado, aunque: ya sea +o −.
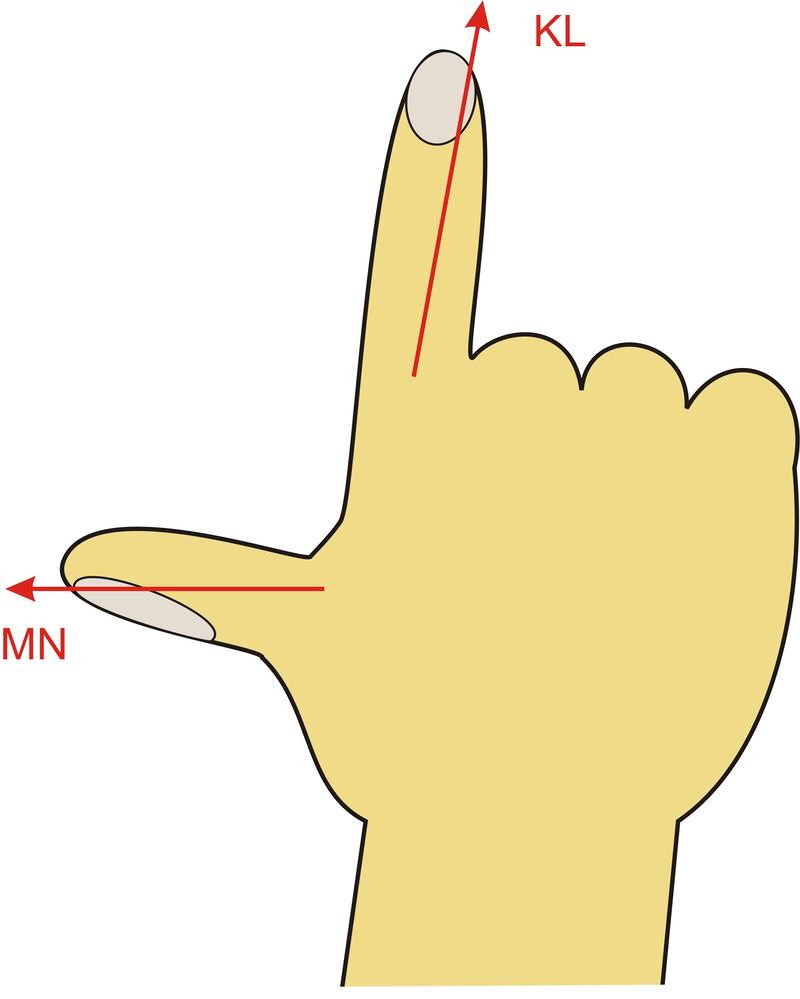
Utilizamos una regla de la mano derecha para indicar la dirección del producto cruzado. Coloca el pulgar y el índice de tu mano derecha con el primer vector a lo largo de tu pulgar y el segundo vector a lo largo de tu dedo índice. Tu dedo medio, cuando se extiende perpendicular a tu palma, te indicará la dirección del producto cruzado de los dos vectores.
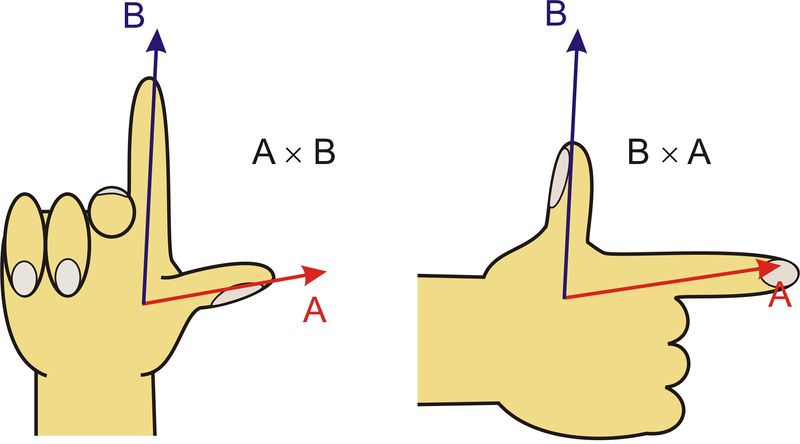
Como puede ver en el diagrama anterior,\(\ \vec{A} \times \vec{B}\) está a lo largo de +( saliendo de la página) mientras que\(\ \vec{B} \times \vec{A}\) está a lo largo de −( bajando a la página) y\(\ \vec{A} \times \vec{B}=-\vec{B} \times \vec{A}\)
El Vector Normal
Podemos usar el producto cruzado y la definición del vector unitario para determinar la dirección que es perpendicular a un plano.
En general, podemos definir un vector normal, n, que tiene una magnitud de unidad (es decir, magnitud igual a uno) y que es perpendicular a un plano ocupado por un par de vectores, U y V.
\(\ \hat{n}=\frac{\vec{U} \times \vec{V}}{|\vec{U} \times \vec{V}|}\)
Ejemplos
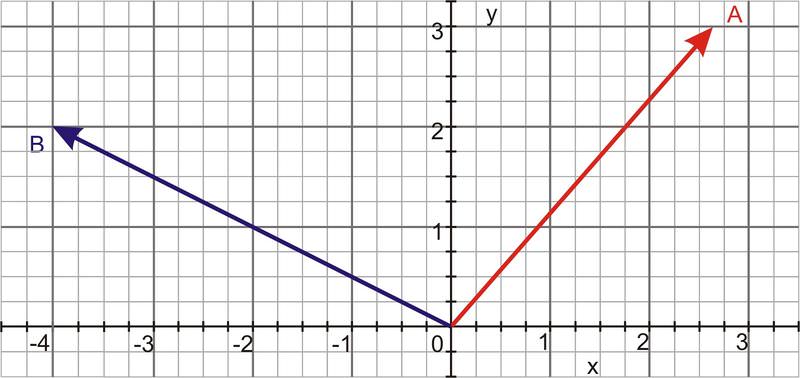
Calcular el producto cruzado de los dos vectores que se muestran a continuación.
Solución
Utilice los componentes de los dos vectores para determinar el producto cruzado.
\(\ \vec{A} \times \vec{B}=\left\langle\left(A_{y} B_{z}-A_{z} B_{y}\right),\left(A_{z} B_{x}-A_{x} B_{z}\right),\left(A_{x} B_{y}-A_{y} B_{x}\right)\right\rangle\)
Dado que estos dos vectores están ambos en el plano x-y, sus propios componentes z son iguales a 0 y el producto vectorial será paralelo al eje z.
\ (\\ begin {array} {l}
\ vec {A}\ veces\ vec {B} =\ langle [(3\ cdot 0) - (0\ cdot 2)], [(0\ cdot-4) - (2.5\ cdot 0)], [(2.5\ cdot 2) - (3\ cdot-4)]\ rangle\
\ vec {A}\ veces\ vec {B} =\ langle [(0) - (0)], [(0) - (0)], [(5) - (-12)]\ rangle=\ langle 0,0, (5+12)\ rangle=\ langle 0,0,17\ rangle
\ end { matriz}\)
Podemos verificar nuestra respuesta usando la versión sinusoidal del producto cruzado, pero primero necesitamos conocer el ángulo entre los dos vectores. Podemos usar el producto punto para encontrar θ. Primero usa los componentes para encontrar el producto punto.
\(\ \vec{A} \times \vec{B}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z}=(2.5 *-4)+(3 * 2)+(0 * 0)=-10+6+0=-4\)
Luego encuentra las magnitudes de los dos vectores:
\ (\\ begin {array} {l}
|\ vec {A} |=\ sqrt {A_ {x} ^ {2} +A_ {y} ^ {2} +A_ {z} ^ {2}} =\ sqrt {2.5^ {2} +3^ {2} +0^ {2}} =\ sqrt {6.25+9+0} =\ sqrt {6.25+9+0} =\ sqrt {6.25+9+0} =\ sqrt {15.25}\\
|\ vec {B} |=\ sqrt {B_ {x} ^ {2} +B_ {y} ^ {2} +B_ {z} ^ {2}} =\ sqrt {(-4) ^ {2} +2^ {2} +0^ {2}} =\ sqrt {16+4+0} =\ sqrt {20}
\ final matriz}\)
Luego usa estas magnitudes con la versión coseno del producto punto para encontrar θ.
\ (\\ comenzar {array} {l}
\ vec {A}\ veces\ vec {B} =|A||B|\ cos\ theta\
-4=\ sqrt {15.25}\ sqrt {20}\ cos\ theta\
\ cos\ theta =\ frac {-4} {\ sqrt {305}}\ approx\ frac {-4} {17.5} =-0.229\\
\ theta=103^ {\ circ}
\ end {array}\)
Ahora usa el seno de este ángulo y las dos magnitudes para determinar el producto cruzado:
\ (\\ begin {array} {l}
|\ vec {A}\ veces\ vec {B} |=|\ vec {A} ||\ vec {B} |\ sin\ theta\
|\ vec {A}\ veces\ vec {B} |=\ sqrt {15.25}\ sqrt {20}\ sin 103^ {\ circ} =\ sqrt {305}\ sin 103^ {\ circ} =17
\ final {array}\)
Esta es la misma respuesta que obtuvimos de la notación de componentes, lo cual es bueno. Utilizamos la regla de la derecha para determinar la dirección del producto vectorial. Si colocas tu pulgar a lo largo del vector A y tu dedo índice a lo largo del vector B, tu dedo medio apuntará a lo largo de +y\(\ |\vec{A} \times \vec{B}|=\langle 0,0,17\rangle\)
El diagrama muestra dos vectores A y B que definen un plano que pasa por el origen. Utilice estos dos vectores para determinar el vector normal a este plano. \(\ \vec{A}=\langle 3,0,4\rangle\)y\(\ \vec{B}=\langle 5,10,0\rangle\)
Solución
El vector normal se define por
\(\ \hat{n}=\frac{\vec{U} \times \vec{V}}{|\vec{U} \times \vec{V}|}\)
En este caso, obtenemos
\(\ \hat{n}=\frac{\vec{A} \times \vec{B}}{|\vec{A} \times \vec{B}|}\)
Utilice la versión de componentes de la ecuación de productos cruzados para encontrar los componentes de\(\ \vec{A} \times \vec{B}\)
\ (\\ comenzar {matriz} {l}
\ vec {A}\ veces\ vec {B} =\ izquierda\ langle\ izquierda (A_ {y} B_ {z} -A_ {z} B_ {y}\ derecha),\ izquierda (A_ {z} B_ {x} -A_ {x} B_ {z}\ derecha),\ izquierda (A_ {x} -A_ {x} B_ {z}\ derecha),\ izquierda (A_ {x}} B_ {y} -A_ {y} B_ {x}\ derecha)
\ derecha\ rangle\\ vec {A}\ veces\ vec {B} =\ langle [(0\ cdot 0) - (4\ cdot 10)], [(4\ cdot 5) - (3\ cdot 0)], [(3\ cdot 10) - (0\ cdot 5)]\ rangle\
\ vec {A}\ veces\ vec {B} =\ langle (0-40), (20-0), (30-0)\ rangle=\ langle-40,20,30\ rangle
\ end {array}\)
A continuación, calcular la magnitud del producto cruzado,\(\ |\vec{A} \times \vec{B}|\)
\ (\\ begin {array} {l}
|\ vec {A}\ veces\ vec {B} |=\ sqrt {(-40) ^ {2} +20^ {2} +30^ {2}} =\ sqrt {1600+400+900} =\ sqrt {2900} =53.8516\
\ sombrero {n} =\ frac {\ vec {A}\ tiempos\ vec {B}} {|\ vec {A}\ veces\ vec {B} |} =\ frac {\ langle-40,20,30\ rangle} {53.9} =\ izquierda\ langle\ frac {-40} {53.9},\ frac {20} {53.9},\ frac {30} {53.9}\ derecha\ rangle=\ langle-0.743,0.371,0.557\ rangle
\ end {array}\)
Determinar el producto cruzado\(\ \vec{F} \times \vec{r}\) para los dos vectores\(\ \vec{F}=\langle 2,3,4\rangle\) y\(\ \vec{r}=\langle 7,6,5\rangle\). Luego usa el producto cruzado para determinar el ángulo entre los dos vectores.
Solución
Una de las dos formas de determinar la magnitud del producto cruzado de dos vectores utiliza los componentes de los dos vectores:
\ (\\ comenzar {matriz} {l}
\ vec {F}\ veces\ vec {r} =\ izquierda\ langle\ izquierda (F_ {y} r_ {z} -F_ {z} r_ {y}\ derecha),\ izquierda (F_ {z} r_ {x} -F_ {x} r_ {z}\ derecha),\ izquierda (F_ {x} -F_ {x} r_ {z}\ derecha),\ izquierda (F_ {x}} r_ {y} -F_ {y} r_ {x}\ derecha)
\ derecha\ rangle\\ vec {F}\ veces\ vec {r} =\ langle (3\ cdot 5-4\ cdot 6), (4\ cdot 7-2\ cdot 5), (2\ cdot 6-3\ cdot 7)\ rangle=\ langle (15-24), (28-10), (12-21)\ rangle\
\ vec {F}\ veces\ vec {r} =\ langle-9,18, -9\ rangle
\ end {array}\)
Ahora podemos usar el producto cruzado y la segunda definición del producto cruzado para determinar el ángulo entre los dos vectores.
\(\ |\vec{F} \times \vec{r}|=|F||r| \sin \theta\)
Necesitamos calcular las magnitudes de los vectores y del producto cruzado.
\ (\\ begin {array} {l}
|\ vec {F} |=\ sqrt {F_ {x} ^ {2} +F_ {y} ^ {2} +F_ {z} ^ {2}} =\ sqrt {2^ {2} +3^ {2} +4^ {2}} =\ sqrt {4+9+16} =\ sqrt {29} =5.385\\
|\ vec {r} |=\ sqrt {r_ {x} ^ {2} +r_ {y} ^ {2} +r_ {z} ^ {2}} =\ sqrt {7^ {2} +6^ {2} +5^ {2}} =\ sqrt {49+36+25} =\ sqrt {110} =10.488\\
|\ vec {F}\ veces\ vec {r} |=\ sqrt {(-9 ) ^ {2} +18^ {2} + (-9) ^ {2}} =\ sqrt {81+324+81} =\ sqrt {486} =22.0454\\
\ sin\ theta=\ frac {|\ vec {F}\ veces\ vec {r} |} {|F||R|} =\ frac {22.0454} {(5.385) (10.488)} =0.390\
\ theta=\ sin ^ {-1} (0.390) =22.98^ {\ circ}
\ end {array}\)
Podemos usar el producto punto de los dos vectores para verificar nuestra solución.
\ (\\ comenzar {matriz} {l}
\ vec {F}\ veces\ vec {r} =|\ vec {F}\ |\ vec {r} |\ cos\ theta\
\ vec {F}\ veces\ vec {r} =F_ {x} r_ {x} +F_ {y} r_ {y} +F_ {z} r_ {z} =2 * 7+3 * 6+4 * 5=14+18+20=52\\
\ cos\ theta=\ frac {\ vec {F}\ veces\ vec {r}} {|\ vec {F} ||\ vec {r} |} =\ frac {52} {(5.385) (10.488)} =0.920714 \
\ theta=\ cos ^ {-1} (0.920714) =22.97
\ end {array}\)
Esta respuesta coincide con nuestro valor desde el producto cruzado hasta dentro de las variaciones de redondeo.
Determinar la magnitud del producto cruzado de los dos vectores que se muestran a continuación.
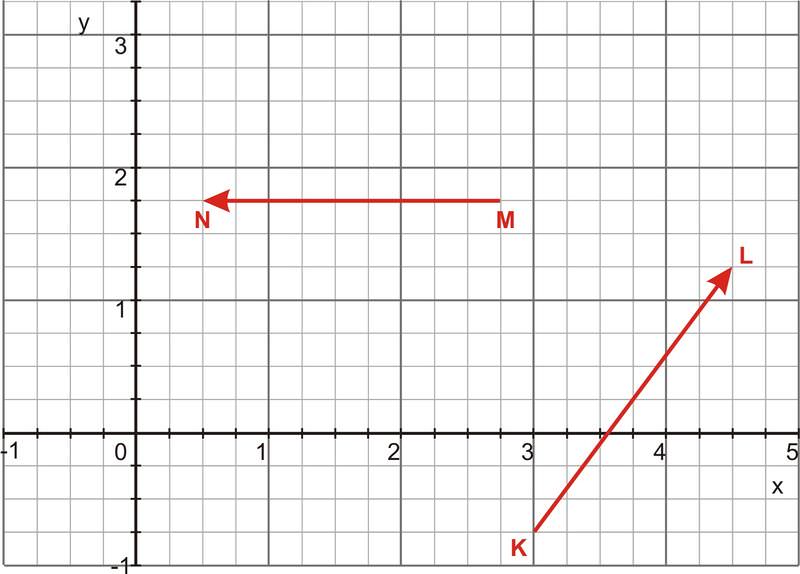
Solución
Primero necesitamos identificar los componentes de los dos vectores usando la información dada en la gráfica. En este caso,\(\ \overrightarrow{M N}=\langle-2.25,0,0\rangle\) y\(\ \overrightarrow{K L}=\langle 1.5,2,0\rangle\)
\ (\\ comenzar {matriz} {l}
\ overrightarrow {M N}\ veces\ overrightarrow {K L} =\ izquierda\ langle\ izquierda (M N_ {y} K L_ {z} -M N_ {z} K L_ {y}\ derecha),\ izquierda (M N_ {z} K L_ {x} -M N_ {x} K L_ {z}\ derecha),\ izquierda (M N_ {x} K L_ {y} -M N_ {y} K L_ {x}\ derecha)\ derecha\ rangle\
\ overrightarrow {M N}\ veces\ overrightarrow {K L} =\ langle (0\ cdot 0-0\ cdot 2), (0\ cdot 1.5- (-2.25)\ cdot 0), ((-2.25)\ cdot 2-0\ cdot 1.5)\ rangle\
\ overrightarrow {M N}\ veces\ overrightarrow {K L} =\ langle 0-0,0-0, -4.5-0\ rangle=\ langle 0,0, -4.5\ rangle
\ end {array}\)
Como podemos ver por los componentes, este vector tiene una magnitud de 4.5 unidades y se encuentra en la dirección —z. También podemos usar la regla de la mano derecha para ver la dirección del producto cruzado. Como se muestra en la siguiente figura, si alineamos el pulgar derecho con el vector MN y el dedo índice derecho con el vector KL, la palma y el dedo medio extendido apuntan en la dirección —z.
Un plano que pasa por el origen se define por los dos vectores,\(\ \vec{W}=\langle 4,5,2\rangle\) y\(\ \vec{L}=\langle 8,1,9\rangle\). Determinar la ecuación de un vector unitario que representa una dirección perpendicular a este plano.
Solución
Para resolver este problema necesitamos usar la definición del vector normal\(\ \hat{n}=\frac{\vec{W} \times \vec{L}}{|\vec{W} \times \vec{L}|}\), la forma componente de la definición del producto cruzado,
\ (\\ comenzar {alineado}
&\ vec {W}\ veces\ vec {L} =\ izquierda\ langle\ izquierda (W_ {y} L_ {z} -W_ {z} L_ {y}\ derecha),\ izquierda (W_ {z} L_ {x} -W_ {x} L_ {z}\ derecha),\ izquierda (W_ {x} _ {y} -W_ {y} L_ {x}\ derecha)\ derecha\ rangle. \ text {En este caso, obtenemos}\\
&\ vec {W}\ veces\ vec {L} =\ langle (5\ cdot 9-2\ cdot 1), (2\ cdot 8-4\ cdot 9), (4\ cdot 1-5\ cdot 8)\ rangle\\
&\ vec {W}\ veces\ vec {L} =\ langle (45-2), (16-36), (4-40)\ rangle=\ langle 43, -20, -36\ rangle
\ end {alineado}\)
También necesitamos conocer la magnitud de este producto cruzado
\ (\\ begin {array} {l}
|\ vec {W}\ veces\ vec {L} |=\ sqrt {x^ {2} +y^ {2} +z^ {2}} =\ sqrt {(43) ^ {2} + (-20) ^ {2} + (-36) ^ {2}} =\ sqrt {1849+400+1296} =\\
\ sqrt {3545} =59.54
\ end {array}\)
Ahora podemos determinar el vector normal
\(\ \hat{n}=\frac{\vec{W} \times \vec{L}}{|\vec{W} \times \vec{L}|}=\frac{\langle 43,-20,-36\rangle}{59.54}=\left\langle\frac{43}{59.54}, \frac{-20}{59.54}, \frac{-36}{59.54}\right\rangle=\langle 0.7222,-0.3359,-0.6046\rangle\)
Determinar el área de un paralelogramo cuyos lados están definidos por los vectores\(\ \vec{w}=\langle 85,89,91\rangle\) y\(\ \vec{h}=\langle 67,70,88\rangle\), longitudes medidas en centímetros.
Solución
El área del paralelogramo cuyos lados están definidos por un par de vectores es igual a la magnitud del producto cruzado de los dos vectores,\(\ |\vec{w} \times \vec{h}|\). Primero tenemos que encontrar el producto cruzado de los dos vectores:
\ (\\ comenzar {matriz} {l}
\ vec {w}\ veces\ vec {h} =\ izquierda\ langle\ izquierda (w_ {y} h_ {z} -w_ {z} h_ {y}\ derecha),\ izquierda (w_ {z} h_ {x} -w_ {x} h_ {z}\ derecha),\ izquierda (w_ {x} -w_ {x} h_ {z}\ derecha),\ izquierda (w_ {x}} h_ {y} -w_ {y} h_ {x}\ derecha)
\ derecha\ rangle\\ vec {w}\ veces\ vec {h} =\ langle (89\ cdot 88-91\ cdot 70), (91\ cdot 67-85\ cdot 88), (85\ cdot 70-89\ cdot 67)\ rangle\
\ vec {w}\ veces\ vec {h} =\ langle (7832-6370), (6097-7480), (5950-5963)\ rangle=\ langle 1462, -1383, -13\ rangle\\
|\ vec {w}\ veces\ vec {h} |=\ sqrt {x^ {2} +y^ {2} +z^ {2}} =\ sqrt {1462^ {2} + (-1383) ^ {2} + (13) ^ {2}} =\ sqrt {4050302}\ aprox 2012.5
\ end {array}\)
Dado que las longitudes de los dos vectores se midieron en centímetros, el área del paralelogramo es de 2013 cm 2 medida al centímetro cuadrado más cercano.
Determinar el producto cruzado de los dos vectores\(\ \vec{f}=\langle 3,13,11\rangle\) y\(\ \vec{g}=\langle 9,6,15\rangle\)
Solución
\ (\\ begin {array} {l}
\ vec {f}\ veces\ vec {g} =\ izquierda\ langle\ izquierda (f_ {y} g_ {z} -f_ {z} g_ {y}\ derecha),\ izquierda (f_ {z} g_ {x} -f_ {x} g_ {z}\ derecha),\ izquierda (f_ {x} -f_ {x} g_ {z}\ derecha),\ izquierda (f_ {x}} g_ {y} -f_ {y} g_ {x}\ derecha)
\ derecha\ rangle\\ vec {f}\ veces\ vec {g} =\ langle (13\ cdot 15-11\ cdot 6), (11\ cdot 9-3\ cdot 15), (3\ cdot 6-13\ cdot 9) \ rangle\\
\ vec {f}\ veces\ vec {g} =\ langle (195-66), (99-45), (18-117)\ rangle=\ langle 129,54, -99\ rangle
\ end {array}\)
Determinar la magnitud del producto cruzado de estos dos vectores.
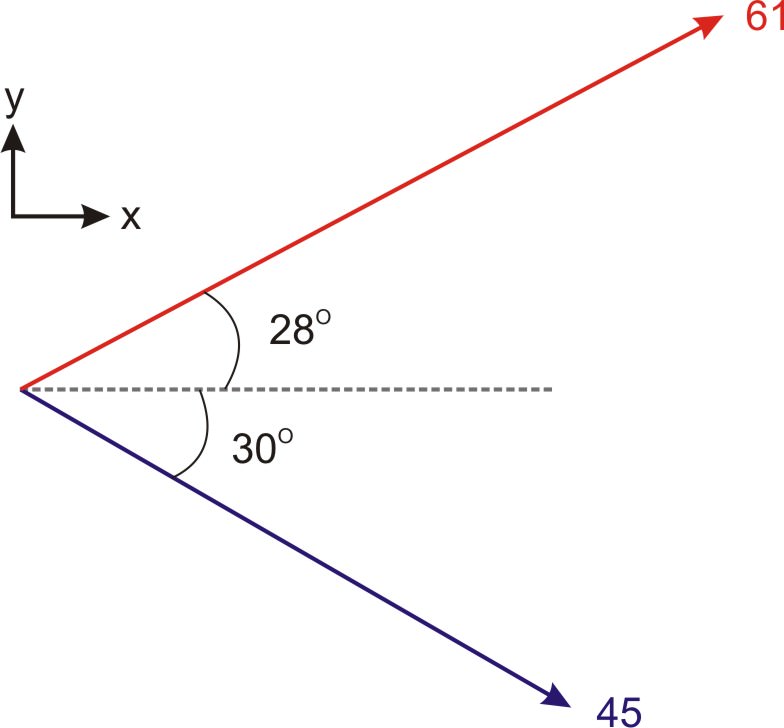
Solución
Como conocemos las magnitudes de los dos vectores y el ángulo entre ellos, podemos usar la versión en ángulo de la ecuación de producto cruzado para determinar la magnitud del producto cruzado:
\(\ |\vec{A} \times \vec{B}|=|\vec{A}||\vec{B}| \sin \theta=(61)(45) \sin 58=2328\)
Dado que estos dos vectores se encuentran en el plano x-y, la dirección del producto cruzado será paralela al eje z.
Revisar
Calcular los productos cruzados:
- Vectores\(\ c=-6 i+2 j+3 k\) y\(\ a=-6 i+2 j+13 k\)
- Vectores\(\ v=\langle-1,4,7\rangle\) y\(\ u=\langle-5,10,3\rangle\)
- Vectores\(\ f=-6 i+8 j-6 k\) y\(\ s=-3 i+15 j+19 k\)
- Vectores\(\ \mathrm{j}=-3 i+15 j-4 k\) y\(\ \mathrm{t}=7 i+10 j+6 k\)
- Vectores\(\ r=\langle 3,13,-1\rangle\) y\(\ v=\langle 7,6,1\rangle\)
- Vectores\(\ e=\langle-1,8,-3\rangle\) y\(\ a=\langle-2,1,19\rangle\)
- Vectores\(\ \mathrm{j}=-3 i+17 j+6 k\) y\(\ h=8 i+9 j+7 k\)
- Vectores\(\ a=9 i+10 j+9 k\) y\(\ g=-5 i+19 j+15 k\)
- Vectores\(\ \mathrm{j}=4 i+18 j-8 k\) y\(\ m=2 i+j+19 k\)
- ¿Cuál es el producto cruzado de\(\ \langle-2,1,-2\rangle\) y\(\ \langle 5,6,9\rangle\)?
- Encuentra un vector ortogonal a ambos\(\ \langle 1,20,2\rangle\) y\(\ \langle 4,2,3\rangle\)
- Vectores\(\ y=5 i+6 j+6 k\) y\(\ f=-4 i+9 j+3 k\). ¿Cuál es el área del paralelogramo formado al tener y y f como lados adyacentes?
- ¿Cuál es el área del paralelogramo formado por tener\(\ \langle-2,1,7\rangle\) y\(\ \langle 5,7,16\rangle\) como lados adyacentes?
- ¿Cuál es el producto cruzado entre\(\ \langle 8,6,8\rangle\) y\(\ \langle 8,6,8\rangle\)?
- Vectores\(\ g=-6 i+9 j-7 k\) y\(\ y=-24 i+36 j-28 k\) ¿Cuál es el producto cruzado entre g e y?
- Un barco navega en una dirección de 89° al este del norte a 564 pies por min. Un viento de cola se suma a la velocidad del avión y sopla 78° al oeste del norte a 25 pies por minuto. Determine la velocidad real del avión en mph.
- Un avión vuela sobre una dirección de 77° al este del sur a 606 mph. Un viento de cola se suma a la velocidad del avión y sopla 33° al oeste del sur a 80 mph. Determinar la dirección del avión.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.6.
El vocabulario
| Término | Definición |
|---|---|
| Productos cruzados | El producto cruzado de dos vectores es un tercer vector que es perpendicular a ambos vectores originales. |
| producto punto | El producto punto también se conoce como producto interno o producto escalar. Las dos formas del producto punto son\(\ \vec{a} \cdot \vec{b}=\|\vec{a}\|\|\vec{b}\| \cos \theta\) y\(\ \vec{a} \cdot \vec{b}=x_{a} x_{b}+y_{a} y_{b}\) |
| vector normal | Un vector normal es un vector que es perpendicular a una superficie o plano dado. Un vector normal unitario es un vector normal con una magnitud de uno. |
| Regla de la mano derecha | La regla de la mano derecha se utiliza para indicar la dirección de un producto cruzado. Coloca el pulgar y el índice de tu mano derecha con el primer vector a lo largo de tu pulgar y el segundo vector a lo largo de tu dedo índice. Tu dedo medio, cuando se extiende perpendicular a tu palma, te indicará la dirección del producto cruzado de los dos vectores. |
| vector de unidad | Un vector unitario es un vector con una magnitud de uno. |