5.4.2: Aplicaciones de Análisis Vectorial
( \newcommand{\kernel}{\mathrm{null}\,}\)
Aplicaciones de análisis vectorial
¿Cuánto trabajo realiza una bola de 10kg rodando por una pendiente de 25 o por 10 yardas?
¿Cómo se puede calcular la fuerza que propulsa un protón a través de un campo magnético?
¿Cómo se podría calcular el par que ejercen los niños en una sierra de ver?
Esta lección trata sobre los usos del análisis vectorial en el mundo real.
Aplicaciones de análisis vectorial
Los vectores pueden ser utilizados por controladores de tráfico aéreo al rastrear aviones, por meteorólogos al describir las condiciones del viento y por programadores informáticos cuando están diseñando mundos virtuales. En esta sección, presentaremos tres aplicaciones de vectores que se utilizan comúnmente en el estudio de la física: trabajo, torque y fuerza magnética.
Trabajo
En física, el término trabajo se utiliza para describir la energía que se agrega o elimina de un objeto o sistema cuando se le aplica una fuerza. A partir del experimento, se ha determinado que el trabajo se maximiza cuando la fuerza aplicada es paralela al movimiento del objeto y que no se realiza ningún trabajo cuando la fuerza se aplica perpendicular al movimiento. Por lo tanto, el trabajo realizado por una fuerza puede ser descrito por el producto puntual del vector de fuerza y el vector de desplazamiento. Por ejemplo, varias fuerzas actúan sobre el esquiador en el siguiente diagrama.
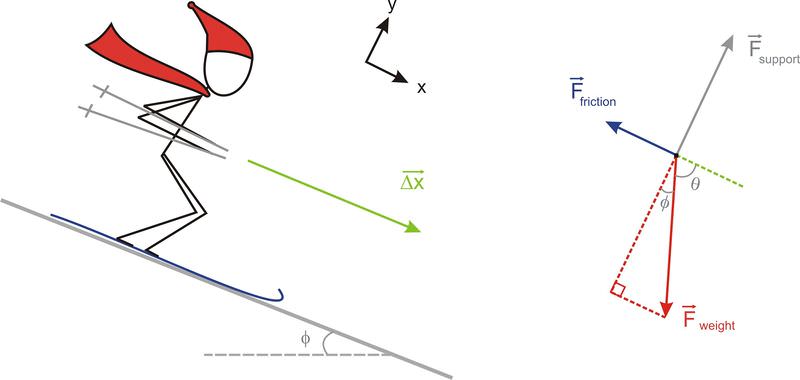
El peso de Sven tira hacia abajo hacia el centro de la tierra, el soporte de nieve es Sven empujando hacia arriba sobre sus esquís perpendiculares a la pendiente, y la fricción entre los esquís de Sven y la nieve apunta en dirección opuesta a su movimiento. El trabajo realizado por cada una de estas fuerzas se puede determinar utilizando el punto producto de la fuerza y el vector de desplazamiento →△x.
\ (\\ begin {array} {l}
W=\ overrightarrow {F}\ times\ overrightarrow {\ triángulo x} =F (\ triángulo x)\ cos\ theta\
W_ {\ texto {fricción}} =\ overrightarrow {F_ {\ text {fricción}}}\ veces\ overrightarrow {\ triángulo x} =\ izquierda (F_ {\ texto {fricción}}\ derecha) (\ triángulo x)\ cos 180^ {\ circ} =-F_ {\ text { fricción}}\ triángulo x\\
W_ {\ texto {soporte}} =\ overrightarrow {F_ {\ text {soporte}}}\ veces\ overrightarrow {\ triángulo x} =( F_ {\ texto {soporte}}) (\ triángulo x)\ cos 90^ {\ circ} =0\
W_ {\ texto {peso}} =\ overrightarrow {F_ {\ text {peso}}}\ veces\ overrightarrow {\ triángulo x} =\ left (F_ {\ text { peso}}\ derecha) (\ triángulo x)\ cos\ theta=\ izquierda (F_ {\ texto {peso}}\ derecha) (\ triángulo x)\ sin\ phi
\ end {array}\)
Fuerza Magnética
La fuerza que ejerce un campo magnético sobre una partícula cargada es más fuerte cuando la partícula se mueve perpendicular al campo y la fuerza magnética sobre la partícula es igual a cero cuando se mueve paralela al campo. Por lo tanto, la fuerza magnética puede describirse usando el producto cruzado del vector de intensidad de campo y el vector de velocidad de la partícula: →F=q→v×→B donde →F está la fuerza sobre la partícula, q es la carga de la partícula, →v es la velocidad de la partícula, y →Bes el vector que representa el campo magnético. Si la velocidad se mide en m/s y si el campo magnético se mide en tesla, la fuerza se medirá en newtons, la unidad base métrica de fuerza.
Torque
Cuando levantas una pelota de béisbol de una mesa, estás ejerciendo una fuerza que mueve el objeto como un todo. Cuando aplicas una fuerza al pomo de una puerta, haces que la puerta gire sobre sus bisagras. Los científicos utilizan el término torque para describir la propiedad similar a la fuerza que afecta la rotación de un objeto. El par puede describirse utilizando el producto cruzado del vector de fuerza y el brazo de palanca, un vector que apunta radialmente hacia afuera desde el eje de rotación hasta el punto donde se aplica la fuerza al objeto: →τ=→r×→F, donde →τ esta el par, →r es el brazo de palanca, y →F es el aplicado fuerza.
Ejemplos
Xiao gira una manivela para bajar un cubo de agua en un pozo. Determinar el trabajo total realizado en el cucharón si el peso del cucharón es de 15 N y la fuerza de tensión en la cuerda es de 13 N. El cucharón se eleva una distancia de 4.5 m mientras está arrancando.
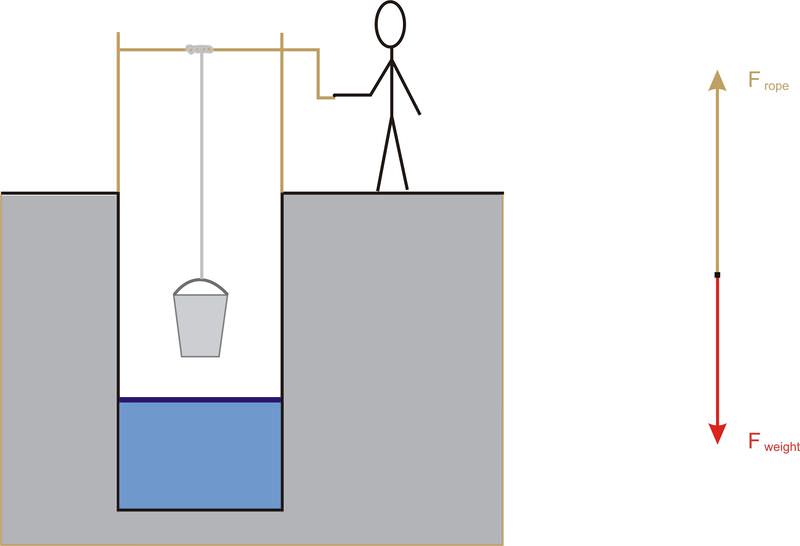
Solución
El trabajo realizado por una fuerza que actúa sobre un objeto es descrito por el producto puntual del vector de fuerza y el vector de desplazamiento: W=→F×→Δx=F(△x)cosθ. En este caso, la cuerda hace trabajo negativo en el cucharón porque el movimiento y la fuerza están en direcciones opuestas. Si la fuerza se mide en newtons y el desplazamiento en metros, el trabajo se mide en julios.
Wrope =→Frope ×→△x=Frope (△x)cosθ=(13N)(4.5m)cos180∘=−58.5J
La fuerza de peso hace un trabajo positivo en el cucharón porque el movimiento y la fuerza están en la misma dirección.
Wweight =→Fweight ×→△x=Fweight (△x)cosθ=(15N)(4.5m)cos0∘=67.5J
El trabajo total es la suma de las dos cantidades individuales de trabajo.
Wtotal =Wrope +Wweight =−58.5+67.5J=9.0J
Se realiza un total de 9.0 J de trabajo en el cucharón a medida que el cucharón se mueve hacia abajo hacia el pozo.
El siguiente diagrama muestra a Sanjay tirando de una caja grande por el piso. Las cuatro fuerzas que actúan sobre la caja durante este proceso se muestran en el siguiente diagrama. ¿Cuál de las cuatro fuerzas ejerce una fuerza distinta de cero sobre la caja?
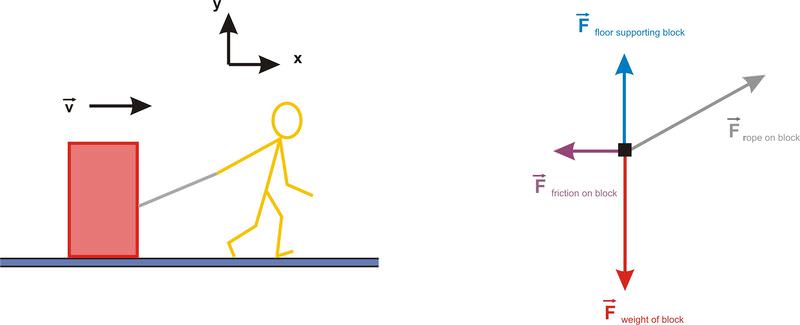
Solución
El producto de punto se define por →A×→B=|A||B|cosθ lo tanto, solo las fuerzas que tienen al menos algún componente paralelo al movimiento harán un trabajo distinto de cero en el objeto. El ángulo θ entre el desplazamiento y las fuerzas perpendiculares al movimiento es de 90 o así →A×→B=|A||B|cosθ=0. La fuerza del piso y el peso de la caja no funcionan, ya que ambas fuerzas son perpendiculares al movimiento de la caja. La cuerda realiza un trabajo positivo en la caja ya que la fuerza de la cuerda sobre la caja tiene un componente x distinto de cero. La fricción hace trabajo negativo en la caja ya que está en la dirección opuesta al desplazamiento.
De'andra está tirando de su pato de juguete (masa 0.75 kg) a una velocidad constante de 3.0 m/s La cuerda que usa para tirar del pato hace un ángulo de 42 o por encima de la horizontal y De'andra mantiene una tensión constante en la cuerda de 2.0 N. Cuál es la cantidad de trabajo que realiza la fuerza de tensión cuando se tira del pato adelantar una distancia de 2.8 m?
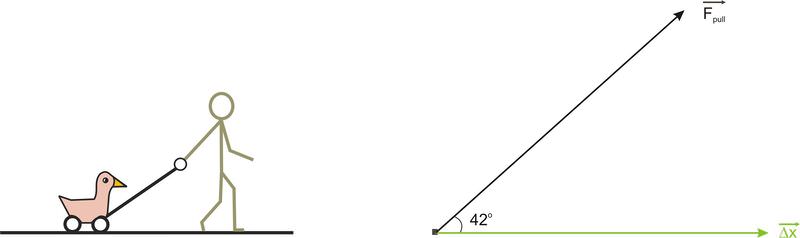
Solución
El trabajo que realiza De'andra sobre el pato depende de la fuerza que utilice para tirar del pato y de la distancia que el pato se mueva mientras tira. También depende del ángulo entre la fuerza de tracción y el vector de desplazamiento.
→Fpull ×→x=|→Fpull ||→x|cosθ=(2.0N)(2.8m)cos42∘=4.16Nm
El N representa “newton”, la unidad de fuerza. La m representa “metros”, la unidad de desplazamiento. (1.0 N) (1.0 m) = 1.0 J donde J representa “julios”, la unidad de trabajo y energía.
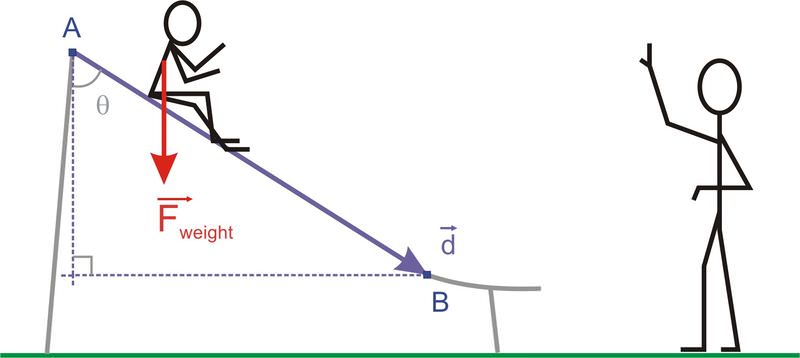
Beuford ha vuelto a llevar a Brynna al parque para jugar en el tobogán. Si Brynna tiene un peso de 25 kg y si el tobogán tiene una inclinación de 30 o por encima de la horizontal, ¿qué trabajo se realiza por su peso mientras se desliza por la pendiente de 3.5 m? Recuerde que la fuerza de peso en newtons es igual al producto de la masa y la aceleración de la gravedad, 9.8 m/s 2.
Solución
Si la diapositiva está inclinada a 30 o por encima de la horizontal, entonces θ = 60 o desde la vertical. El trabajo realizado por una fuerza sobre un objeto viene dado por el punto producto de la fuerza y el desplazamiento del objeto. Aquí →Fweight =mg=(25 kg)(9.8 m/s2)=245 N. Por lo tanto, W=→Fweight ×→d=|→Fweight ||→d|cosθ=(245N)(3.5m)cos60∘=428.75J
Los científicos del Laboratorio Fermi en Chicago, IL, utilizan campos magnéticos para dirigir haces de protones durante sus exploraciones de la estructura submicroscópica de átomos y quarks. Tanto la intensidad del campo magnético como la velocidad de los protones son cantidades vectoriales. Determinar la fuerza sobre un protón que se mueve hacia el norte a 4.2 × 10 6 m/s a través de un campo magnético de 2.5 T orientado de este a oeste. (Nota: los protones son muy pequeños y por lo tanto son capaces de moverse MUY rápido.)
Solución
Defina un sistema de coordenadas donde hacia el este es la dirección +z, hacia el norte es la dirección +y y hacia arriba es la dirección +z. En este sistema de coordenadas, →v=⟨0,4.2×106,0⟩ y →B=⟨−2.5,0,0⟩. Por lo tanto, |→F|=q|→v×→B|=q(|→v||→B|sinθ). Dado que la velocidad es hacia el norte y el campo magnético es hacia el oeste, el ángulo entre los dos vectores es de 90 o.
\ (\\ begin {array} {l}
|\ vec {F} |=q|\ vec {v}\ veces\ vec {B} |=q (|\ vec {v} ||\ vec {B} |\ sin\ theta) =\ left (1.6\ times 10^ {-19}\ right)\ left (\ left (4.2\ times 10^ {6}\ right) (2.5)\ sin 90^ {\ circ}\ derecha) =
16.8\ times 10^ {-13} N
\ end {array}\)
Usando la regla de la mano derecha, podemos determinar la dirección de la fuerza sobre el protón. Si apuntas tu pulgar hacia el norte a lo largo del vector de velocidad y tu dedo índice hacia el oeste a lo largo del vector de campo magnético, tu palma y tu dedo medio extendido apuntan hacia arriba. Por lo tanto, la fuerza que ejerce el campo magnético sobre el protón está en la dirección +z:
|→F|=q→v×→B=⟨0,0,16.8×10−13N⟩.
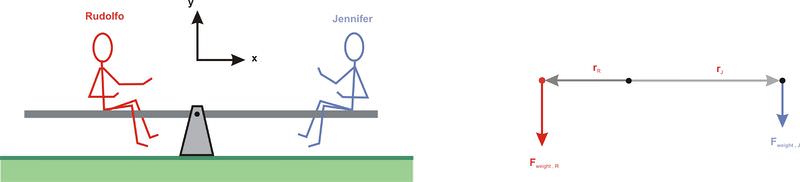
Si dos hijos, Rudolfo (peso = 210 N) y Jennifer (peso = 175 N), se sientan en cualquiera de los extremos de una sierra como se muestra a continuación. Rudolfo está a 1.0 m del pivote y Jennifer a 1.4 m del pivote. ¿Qué pares ejercen los niños sobre la sierra?
Solución
El sistema de coordenadas se ha definido de tal manera que los vectores peso-fuerza son paralelos al eje y y los vectores de brazo de palanca son paralelos al eje x. Primero determine la forma componente de cada ecuación vectorial y luego use la versión componente de la ecuación de productos cruzados para determinar el par ejercido por cada niño.
\ (\\ begin {array} {l}
\ overrightarrow {\ tau_ {R}} =\ overrightarrow {r_ {R}}\ veces\ overrightarrow {F_ {\ text {peso}, R}} =\ langle-1.0\ mathrm {~m}, 0,0\ rangle\ veces\ langle 0, -210 N, 0\ rangle\
\ vec {r}\ veces\ vec {F} =\ izquierda\ langle\ izquierda (r_ {y} F_ {z} -r_ {z} F_ {y}\ derecha),\ izquierda (r_ {z} F_ {x} -r_ {x} F_ {z}\ derecha),\ izquierda (r_ {x} F_ {y} -r_ {y} F_ {x}\ derecha)\ derecha\ rangle\
\ overrightarrow {r_ {R}}\ veces\ overrightarrow {F_ {R}} =\ langle ((0 * 0) - (0 *-210)), (0 * 0) - (-1 * 0)), ((-1 *-210) - (0 * 0))\ rangle=
\ langle 0,0,210 m N\ rangle\
\ overrightarrow {\ tau_ {J}} =\ overrightarrow {r_ {J}}\ veces\ overrightarrow {F_ {\ text {peso,} J}} =\ langle 1.4 m, 0,0\ rangle\ veces\ langle 0, -170 N, 0\ rangle\
\ vec {r}\ veces\ vec {F} =\ izquierda\ langle\ izquierda (r_ {y} F_ {z} -r_ {z} F_ {y}\ derecha),\ izquierda (r_ {z} F_ {x} -r_ {x} F_ {z}\ derecha),\ izquierda (r_ {x} F_ {y} -r_ {y} F_ {x}\ derecha)\ derecha\ rangle\
\ overrightarrow {r_ {J}}\ veces\ overrightarrow {F_ {J}} =\ langle ((0 * 0) - (0 *-170)), ((0 * 0) - (1.4 * 0)), ((1.4 *-170) - (0 * 0))\ rangle=
\ langle 0,0, -238 m N\ rangle
\ end {array}\)
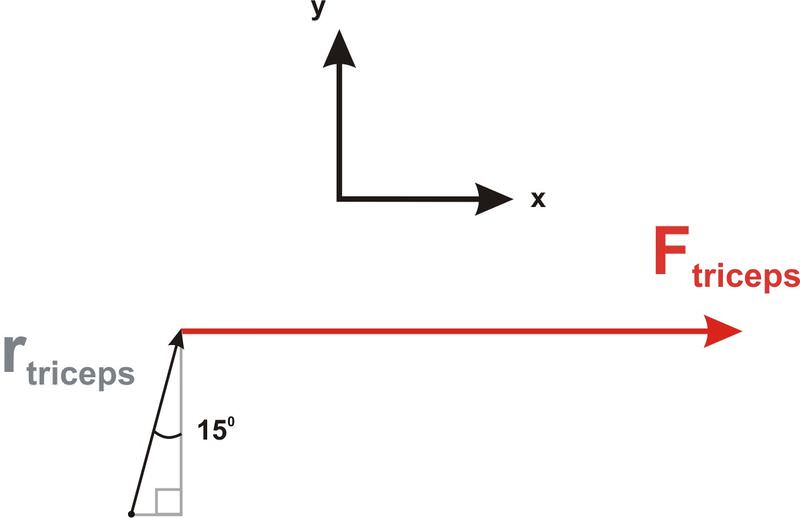
Los científicos del ejercicio y los fisioterapeutas utilizan torque para analizar diversos ejercicios como el ejercicio de tríceps que se muestra en el diagrama a continuación. Aquí, el músculo tríceps ejerce una fuerza sobre el codo-extremo del antebrazo, afectando la rotación del antebrazo. Si el tríceps ejerce una fuerza de 17 N, ¿qué par se aplica al antebrazo?
Solución
Dado que el antebrazo se posiciona en un ángulo de 15 o con respecto a la vertical, el ángulo entre los dos vectores es de 90 o — 15 o = 75 o. La magnitud del vector palanca-brazo es la distancia desde el codo-pivote hasta el punto donde el tríceps tira del hueso, |→r|=2.5 cm. De igual manera, la magnitud del vector de fuerza es la fuerza de la fuerza, |→F|=17N. Dado que conocemos las magnitudes de ambos vectores y el ángulo entre ellos, podemos usar la versión en ángulo de la ecuación de producto cruzado para determinar la magnitud del par.
|→τ|=rFsinθ=(2.5 cm)(17N)sin75=41.05 cm⋅N
Revisar
- Un barco pesquero navega hacia el oeste a una constante de 15 km/h y una corriente de 3 km/h corre con dirección sur. ¿Cuál es la velocidad de la embarcación relativa al fondo del mar?
- Dos topadoras tiran de un árbol grande para sacarlo del camino de una carretera. Una excavadora tira 3000N hacia el oeste y la otra 2500N en dirección sur debido al terreno. Determinar la fuerza resultante que actúa sobre el árbol. Si el árbol tiene una masa de 1000 kg calcula la aceleración del árbol debido a la fuerza resultante que actúa sobre él.
- Tres fuerzas horizontales coplanares cada una de magnitud 10 N actúan sobre un cuerpo de masa de 5 kg como se muestra a continuación. Determinar la magnitud de la fuerza neta que actúa sobre el cuerpo y la magnitud de la aceleración resultante.
- Si el vector A = 5 N norte y el vector B = 10 N este, encuentre el resultante del vector A — vector B.
- Un submarino viaja a 20 km/h con dirección este. Poco después, viaja hacia el norte a 15 km/h Calcular el cambio de velocidad.
- Un avión de combate tiene una verdadera velocidad aérea de 1000 km/h con rumbo este. Hay un viento cruzado que sopla 60 grados al este del sur a 100 km/h Calcular la velocidad del chorro con respecto al suelo.
- Un palé de masa de 10 kg se asienta sobre una superficie horizontal, se ejerce una fuerza sobre el palé por medio de una cadena inclinada a 60° con respecto a la horizontal. Si la tensión en la cadena es de 150 N y la fuerza de fricción entre el palé y la superficie horizontal es de 55 N, ¿se moverá el palé bajo estas condiciones? Explique. Si el palé no se mueve, determina el tamaño de la aceleración con la que se mueve.
- Un automóvil averiado con una masa total de 300 kg es arrastrado por una sola línea de remolque unida a un camión de remolque con una masa de 1000 kg. Si el arrastre sobre el camión y el automóvil es una décima parte de sus respectivos pesos, y la fuerza total hacia adelante ejercida por el camión remolcador es de 5130 kg fuerza (es decir, 5130 x 9.8 N), encuentre la magnitud de: a. la fuerza total que resiste el movimiento hacia adelante del camión y el automóvil; b. la aceleración del sistema camión/automóvil; c. la fuerza aceleradora desequilibrada sobre el carro averiado; d. la tensión en la línea de remolque.
- Un piloto de caza con una masa de MA = 80 kg se sienta en el foso de gallos con la espalda horizontal al suelo. Su chorro se mueve verticalmente con aceleración a. si la aceleración debida a la gravedad en el piloto es g = 9.8 ms-2, escriba una expresión matemática para y calcule el valor de la fuerza de reacción R entre el piloto y el respaldo de su asiento en el jet cuando: a. a = 0; b. a = 8 ms-2 hacia arriba; c. a = 8 ms-2 hacia abajo.
- Un avión vuela 691mph con dirección 13° al este de norte. Un viento de cola sopla 67° al oeste de norte a 92 mph. Determinar la velocidad real del avión con respecto al suelo.
- Un ave se dirige 40° al este del norte a 67 mph. Un viento de cola sopla 45° al oeste del sur a 68 mph. Determinar la dirección del ave.
- Un OVNI se desliza a 516 mph, con dirección 32° al este del sur. Determine la dirección del OVNI si sopla viento de cola 42° al oeste del norte a 29 mph.
- Un cohete vuela 63° al oeste del norte a 575 mph. Determine la dirección real del cohete si sopla un viento de cola 22° al oeste del sur a 78 mph.
- ¿Cuál es la dirección resultante de una lancha rápida que corre a 66.5mph con dirección 80° oeste de sur a 611 mph, si un viento de cola la empuja hacia una dirección 89° este de sur a 4.5 mph?
- Varios malvados villanos sostienen a Spiderman en su lugar con cuerdas. Si Frankie de Nariz Plana está tirando a una fuerza constante de 19 libras, 44° a la horizontal, Gary de Punta Verde está tirando a una fuerza constante de 29 libras a lo largo de 31° a la horizontal, y Jelly-Knee Jennifyr está tirando a una fuerza constante de 26 libras en un ángulo de 33°, Qué tan duro y en qué dirección es Naranja-Chin Oswald tirando si Spiderman está atascado en su lugar?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.11.
vocabulario
| Término | Definición |
|---|---|
| Julios | Los julios son una unidad estándar de energía. Un joule equivale a un Newton-metro. |
| Newtons | Los newtons son una unidad de trabajo estándar. |
| Regla de la mano derecha | La regla de la mano derecha se utiliza para indicar la dirección de un producto cruzado. Coloque el pulgar y el índice de su mano derecha con el primer vector a lo largo del pulgar y el segundo vector a lo largo de su dedo índice. Tu dedo medio, cuando se extiende perpendicular a tu palma, te indicará la dirección del producto cruzado de los dos vectores. |
| par | El término torque se usa para describir la propiedad similar a la fuerza que afecta la rotación de un objeto. |
| Trabajo | El trabajo es una expresión de cuánta energía se necesita para mover un objeto a una distancia. El trabajo se define como fuerza por desplazamiento, y se mide en julios. |



