6.3.1: Gráficas de Hipérbolas Centradas en el Origen
- Page ID
- 108800
Graficar hipérbolas centradas en el origen
Tu tarea es graficar la hipérbola\(\ 9 y^{2}-4 x^{2}=36\). ¿Cuáles son las asíntotas y focos de tu gráfica?
Graficando Hipérbolas
Sabemos que la gráfica resultante de una función racional es una hipérbola con dos ramas. Una hipérbola es también una sección cónica. Para crear una hipérbola, cortarías un plano a través de dos conos invertidos, de tal manera que el plano es perpendicular a las bases de los conos.

Por la definición cónica, una hipérbola es el conjunto de todos los puntos tal que la de las diferencias de las distancias a los focos es constante.
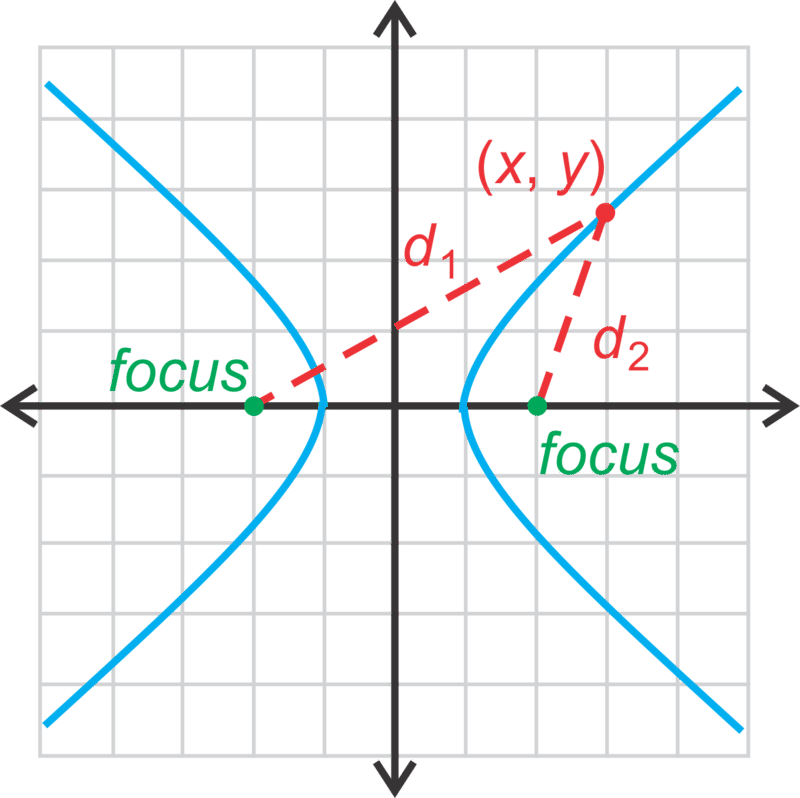
Usando la imagen, cualquier punto,\(\ (x,y)\) en una hipérbola tiene la propiedad,\(\ d_{1}-d_{2}=P\), donde\(\ P\) es una constante.
Comparando esto con la elipse, donde\(\ d_{1}+d_{2}=P\) y la ecuación era\(\ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) o\(\ \frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1\).
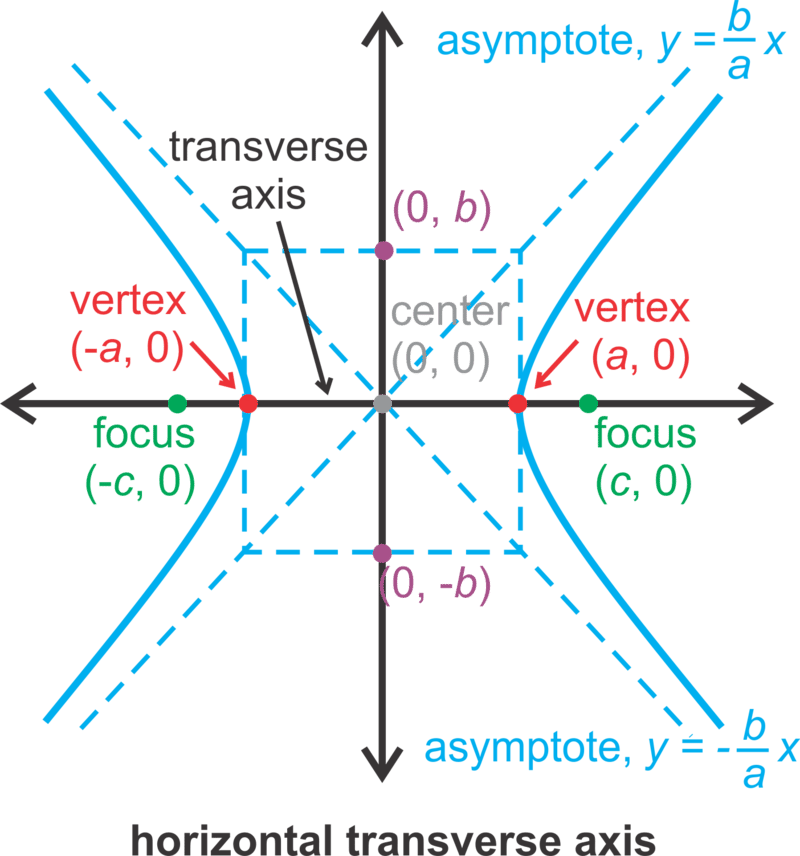
Para una hipérbola, entonces, la ecuación será\(\ \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) o\(\ \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\). Observe en la orientación vertical de una hipérbola, el\(\ y^{2}\) término es primero. Al igual que con una elipse, hay dos vértices, en la hipérbola. Aquí, son los dos puntos que están más cerca uno del otro en la gráfica. La línea a través de los vértices y focos se llama eje transversal. Su punto medio es el centro de la hipérbola. En este concepto, el centro será el origen. Siempre habrá dos ramas para cualquier hipérbola y dos asíntotas.

Vamos a graficar\(\ \frac{x^{2}}{64}-\frac{y^{2}}{25}=1\) y luego encontrar los vértices, focos y asíntotas.
En primer lugar, esta hipérbola tiene un eje transversal horizontal porque el\(\ x^{2}\) término es primero. También, con hipérbolas, el\(\ b\) término\(\ a\) y se mantiene en su lugar, pero los\(\ y\) términos\(\ x\) y cambian. \(\ a\)no siempre es mayor que\(\ b\).
Por lo tanto,\(\ a=\sqrt{64}=8\) y\(\ b=\sqrt{25}=5\). Para graficar esta hipérbola, salga 8 unidades a la izquierda y derecha del centro y 5 unidades arriba y abajo para hacer un rectángulo. Las diagonales de este rectángulo son las asíntotas.
Dibuja las ramas de hipérbola con los vértices en el eje transversal y el rectángulo. Dibuja las ramas para acercarse a las asíntotas, pero no tocarlas.
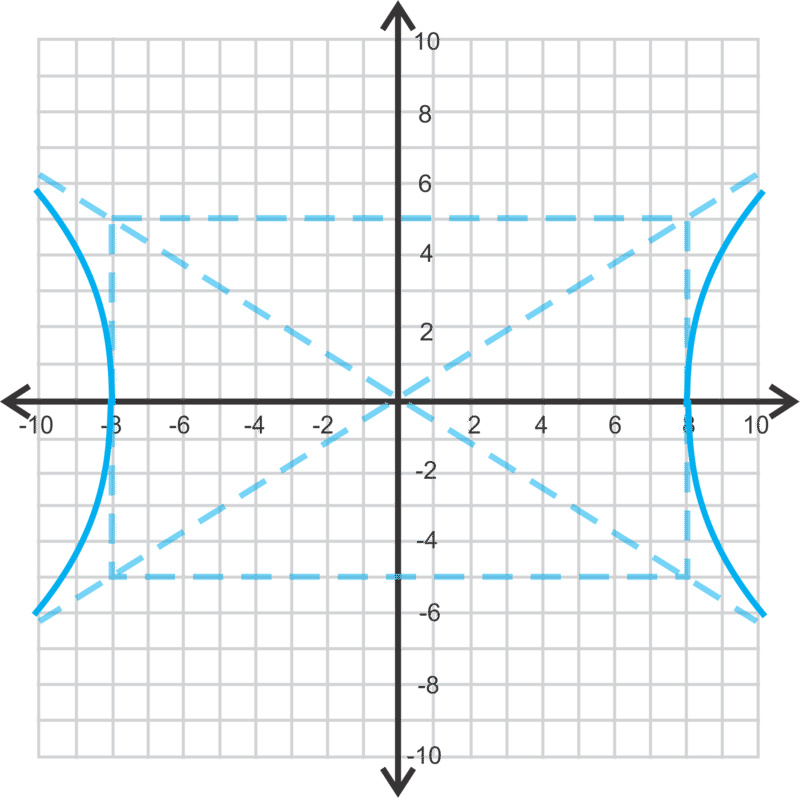
Los vértices son\(\ (\pm 8,0)\) y las asíntotas son\(\ y=\pm \frac{5}{8} x\) (ver imágenes arriba. Para encontrar los focos, utilizamos el Teorema de Pitágoras,\(\ c^{2}=a^{2}+b^{2}\) porque los focos están más alejados del centro que los vértices.
\ (\\ comenzar {alineado}
c^ {2} &=64+25=89\\
c &=\ sqrt {89}
\ end {alineado}\)
Los focos son\(\ (\pm \sqrt{89}, 0)\).
Ahora, graficemos\(\ 36 y^{2}-9 x^{2}=324\) e identifiquemos los focos.
Esta ecuación no está en forma estándar. Para reescribirlo en forma estándar, el lado derecho de la ecuación debe ser 1. Divide todo por 324.
\ (\\ comenzar {alineado}
\ frac {36 y^ {2}} {324} -\ frac {9 x^ {2}} {324} &=\ frac {324} {324}\
\ frac {y^ {2}} {9} -\ frac {x^ {2}} {36} &=1
\ end {alineado}\)
Ahora, podemos ver que se trata de una hipérbola vertical, dónde\(\ a=3\) y\(\ b=6\). Dibuja el rectángulo, asíntotas y traza los vértices en el\(\ y \text { -axis }\).
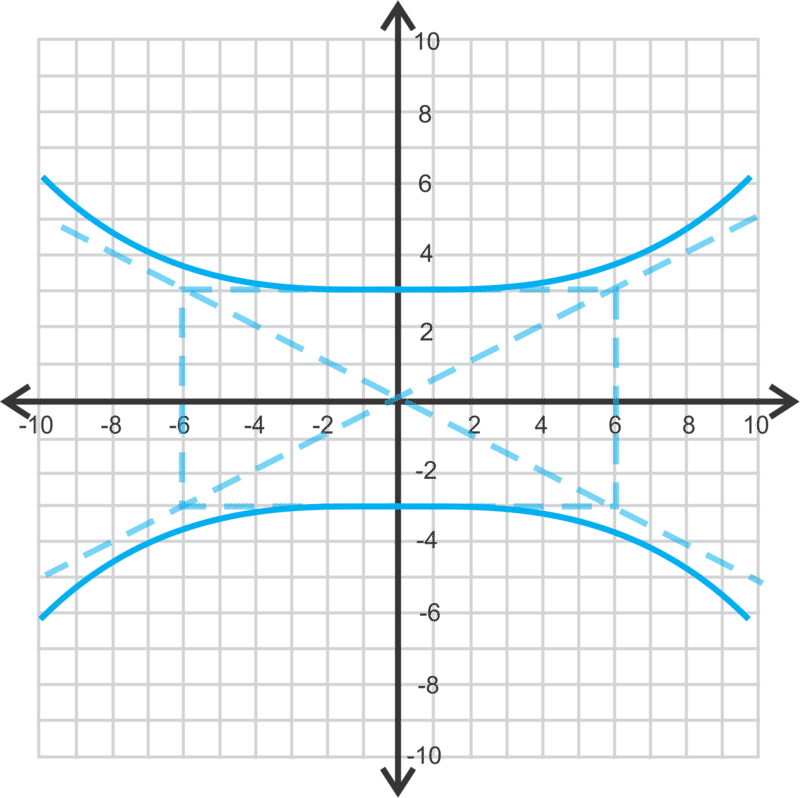
Para encontrar los focos, use\(\ c^{2}=a^{2}+b^{2}\).
\ (\\ begin {array} {l}
c^ {2} &=36+9=45\\
c&=\ sqrt {45} =3\ sqrt {5}
\ end {array}\)
Los focos son\(\ (0,3 \sqrt{5})\) y\(\ (0,-3 \sqrt{5})\)
Finalmente, graficemos\(\ \frac{x^{2}}{4}-\frac{y^{2}}{4}=1\) e identifiquemos las asíntotas.
Esta será una hipérbola horizontal, porque la\(\ x \text { -term }\) es la primera. \(\ a\)y ambos\(\ b\) serán 2 porque\(\ \sqrt{4}=2\). Dibuja el cuadrado y las diagonales para formar las asíntotas.
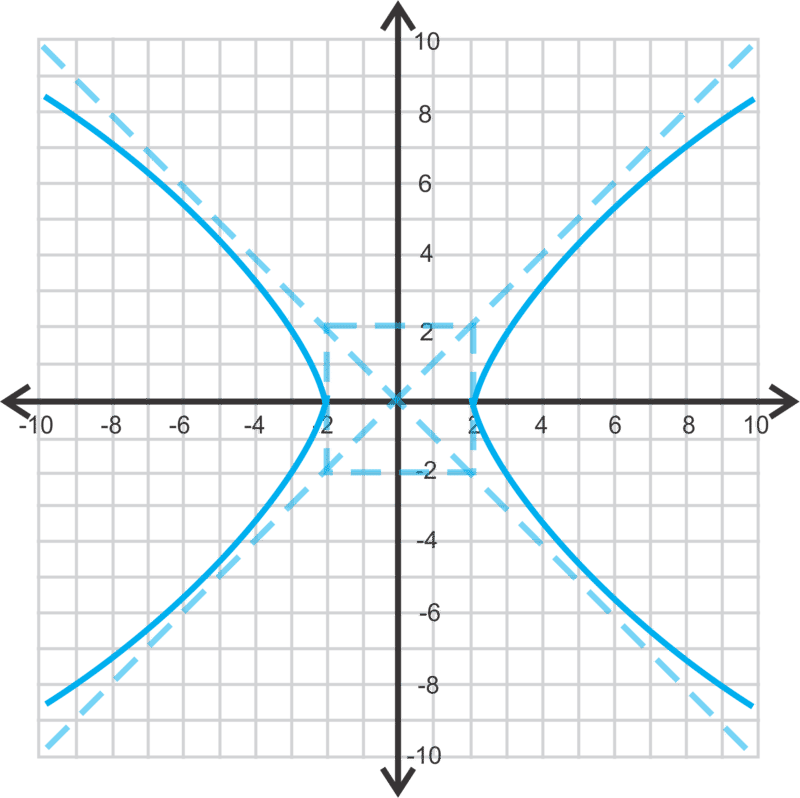
Las asíntotas son\(\ y=\pm \frac{2}{2} x\) o\(\ y=x\) y\(\ y=-x\).
Nota Importante: Las asíntotas y el cuadrado no forman parte de la función. Se incluyen en graficar una hipérbola porque facilita hacerlo.
Además, al graficar hipérbolas, estamos dibujando cada rama. No hicimos una tabla de valores para encontrar ciertos puntos y luego conectarnos. Puedes hacer esto, pero usar el cuadrado o rectángulo con las asíntotas produce una gráfica bastante precisa y es mucho más simple.
Ejemplos
Anteriormente, se le pidió que encontrara las asíntotas y focos de su gráfica.
Solución
Primero, necesitamos obtener la ecuación en la forma\(\ \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\), así que divide por 36.
\ (\\ begin {array} {l}
9 y^ {2} -4 x^ {2} &=36\
\\ frac {9 y^ {2}} {36} -\ frac {4 x^ {2}} {36} &=\ frac {36} {36}\
\ frac {y^ {2}} {4} -\ frac {x^ {2} {9} &=1
\ end {array}\)
Ahora podemos ver eso\(\ a^{2}=4\) y\(\ b^{2}=9\), así\(\ a=2\) y\(\ b=3\). Además, debido a que\(\ y \text { -term }\) lo primero viene, la hipérbola está orientada verticalmente. Por lo tanto, las asíntotas son\(\ y=-\frac{a}{b} x\) y\(\ y=\frac{a}{b} x\).
Sustituyendo\(\ a\) y\(\ b\), obtenemos\(\ y=-\frac{2}{3} x\) y\(\ y=\frac{2}{3} x\).
Por último, para encontrar los focos, use\(\ c^{2}=a^{2}+b^{2}\).
\ (\\ begin {array} {l}
c^ {2} &=4+9=13\\
c&=\ sqrt {13}
\ end {array}\)
Los focos son\(\ (0, \sqrt{13})\) y\(\ (0,-\sqrt{13})\).
Encuentra los vértices, focos, y asíntotas de\(\ y^{2}-\frac{x^{2}}{25}=1\).
Solución
Primero, reescribamos la ecuación así:\(\ \frac{y^{2}}{1}-\frac{x^{2}}{25}=1\). Sabemos que el eje transversal es vertical porque el\(\ y \text { -term }\) es primero, haciendo\(\ a=1\) y\(\ b=5\). Por lo tanto, los vértices son\(\ (0,−1)\) y\(\ (0,1)\). Las asíntotas son\(\ y=\frac{1}{5} x\) y\(\ y=-\frac{1}{5} x\). Por último, encontremos los focos usando\(\ c^{2}=a^{2}+b^{2}\).
\ (\\ begin {array} {l}
c^ {2} &=1+25=26\\
c&=\ sqrt {26}
\ end {array}\)
Los focos son\(\ (0,-\sqrt{26})\) y\(\ (0, \sqrt{26})\)
Gráfico Ejemplo 2.
Solución
Gráfica\(\ 9 x^{2}-49 y^{2}=411\).
Solución
Reescribe la ecuación para que el lado derecho sea igual a 1. Divide todo por 441.
\ (\\ comenzar {alineado}
\ frac {9 x^ {2}} {441} -\ frac {49 y^ {2}} {441} &=\ frac {441} {441}\
\ frac {x^ {2}} {49} -\ frac {y^ {2}} {9} &=1
\ end {alineado}\)
\(\ a=9\)y\(\ b=6\) con un eje transversal horizontal.
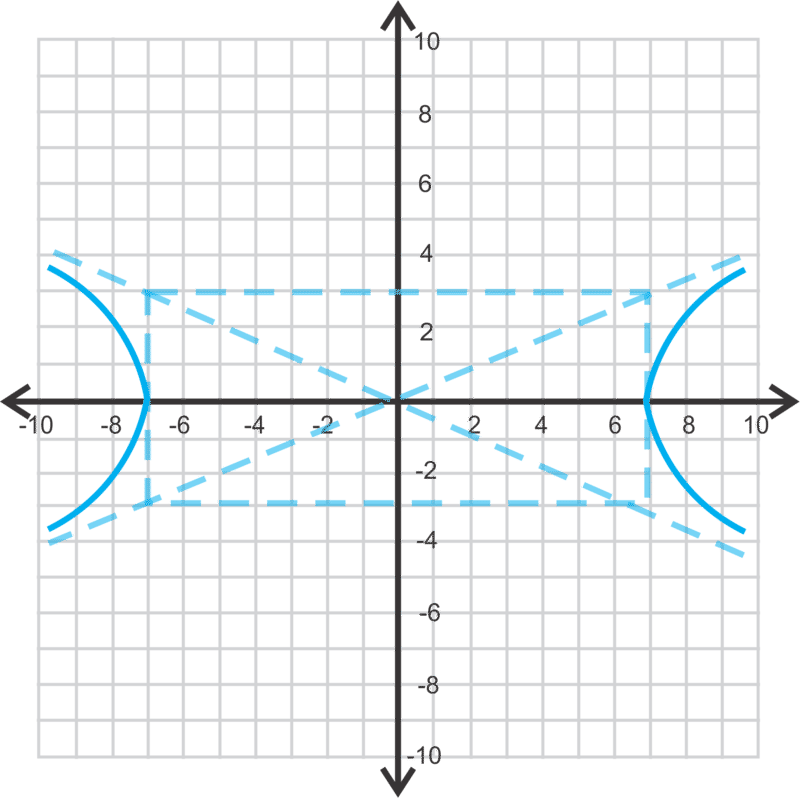
Revisar
Encuentra los vértices, asíntotas y focos de cada hipérbola a continuación.
- \(\ \frac{x^{2}}{9}-\frac{y^{2}}{16}=1\)
- \(\ 4 y^{2}-25 x^{2}=100\)
- \(\ \frac{x^{2}}{81}-\frac{y^{2}}{64}=1\)
- \(\ x^{2}-y^{2}=16\)
- \(\ \frac{y^{2}}{49}-\frac{x^{2}}{25}=1\)
- \(\ 121 y^{2}-9 x^{2}=1089\)
- \(\ y^{2}-x^{2}=1\)
- \(\ \frac{x^{2}}{64}-\frac{y^{2}}{4}=1\)
- \(\ \frac{y^{2}}{4}-\frac{x^{2}}{64}=1\)
- Gráfica #1.
- Gráfica #2.
- Gráfica #8.
- Gráfica #9.
- Redacción Compara las hipérbolas de #8 y #9. ¿Cómo son iguales? ¿En qué se diferencian? ¿Qué sabes de las asíntotas y focos?
- Pensamiento crítico Comparar las ecuaciones\(\ \frac{x^{2}}{25}-\frac{y^{2}}{9}=1\) y\(\ \frac{x^{2}}{25}+\frac{y^{2}}{9}=1\). Gráficalos en los mismos ejes y encuentra sus focos.
Respuestas para problemas de revisión
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.7.
Atribuciones de imagen
- [Figura 1]
Crédito: Derechos de autor de la imagen DVARG, 2014, modified by CK-12 Foundation; CK-12 Foundation
Fuente: http://www.shutterstock.com
Licencia: Licencia de Shutterstock; CC BY-SA

