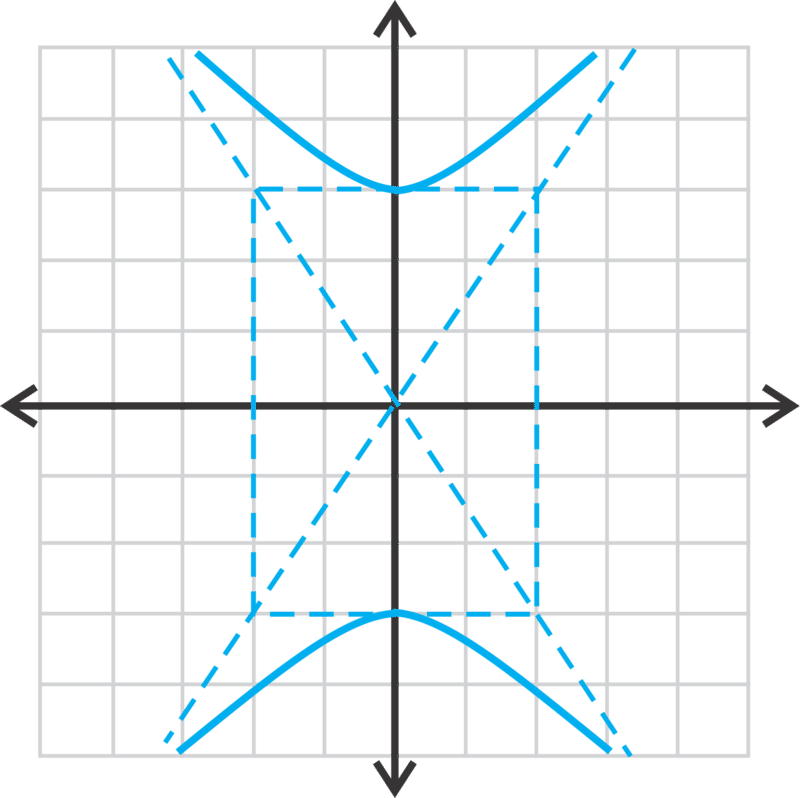
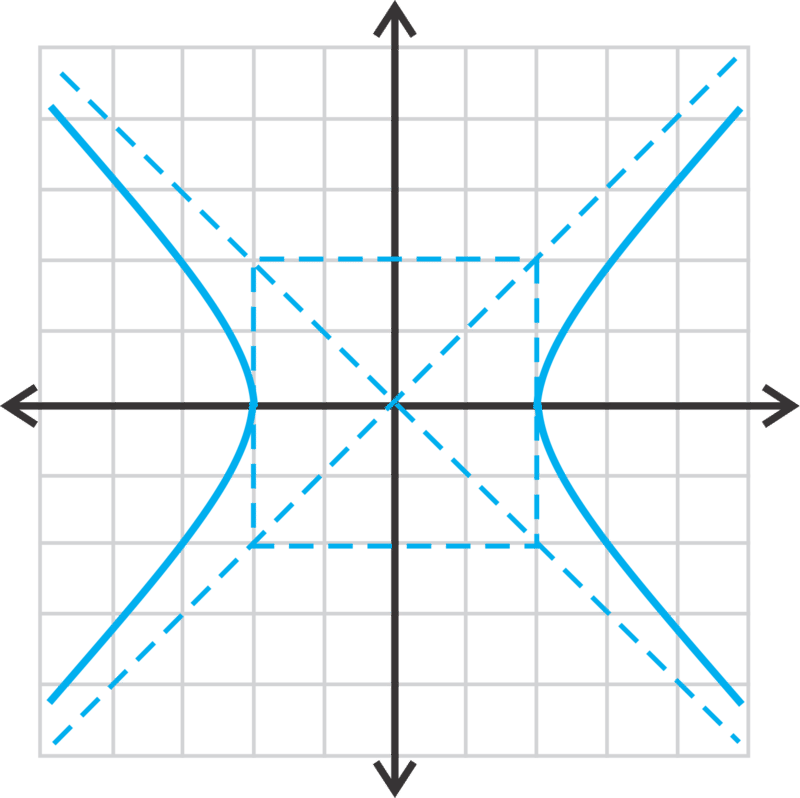
6.3.2: Ecuaciones de Hipérbolas Centradas en los Orígenes

Última actualización
Guardar como PDF

Page ID: 108783

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Escribir la ecuación de una hipérbola, centrada en el origen

Se te pide que resuelvas un acertijo. Se te dan los siguientes datos para ayudarte.

Soy una hipérbola centrada en el origen.
Mi vértice es (0, −2).
Uno de mis focos es (0, −3).

¿Cuál es mi ecuación?

La ecuación de una hipérbola

En este concepto, vamos a trabajar hacia atrás y encontrar la ecuación de hipérbolas, dadas ciertas piezas de información. Para todo este concepto, la hipérbola se centrará en el origen.

Encontremos la ecuación de la hipérbola, centrada en el origen, con un vértice de (−4, 0) y foco de (−6, 0).

Debido a que el vértice y el foco están en el\(\ x \text {-axis }\), sabemos que el eje transversal es horizontal.

Por lo tanto, la ecuación será\(\ \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\). Desde el vértice, lo sabemos\(\ a=4\) y\(\ c=6\). Vamos a resolver para\(\ b^{2}\) usar\(\ c^{2}=a^{2}+b^{2}\).

\ (\\ begin {array} {l}
6^ {2} =4^ {2} +b^ {2}\\
36=16+b^ {2}\ fila derecha b^ {2} =20
\ end {array}\)

La ecuación de la hipérbola es\(\ \frac{x^{2}}{16}-\frac{y^{2}}{20}=1\).

Ahora, encontremos la ecuación de la hipérbola, centrada en el origen, con una asíntota de\(\ y=\frac{2}{3} x\) y vértice de\(\ (0,12)\).

Sabemos que\(\ a=12\), hacer que el eje transversal sea vertical y la ecuación general de la asíntota\(\ y=\frac{a}{b} x\). Por lo tanto\(\ \frac{2}{3}=\frac{12}{b}\),, haciendo\(\ b=18\). Por lo tanto, la ecuación de la hipérbola es\(\ \frac{y^{2}}{144}-\frac{x^{2}}{324}=1\).

En este problema, demostramos que la pendiente de la asíntota se puede reducir a algo que no siempre es\(\ \frac{a}{b}\), sino\(\ c\left(\frac{m}{n}\right)=\frac{a}{b}\), donde\(\ c\) hay alguna constante en la que podemos reducir la fracción.

Finalmente, encontremos las ecuaciones de dos hipérbolas con una asíntota de\(\ y=-\frac{5}{9} x\).

Esta asíntota puede ser para una hipérbola vertical u horizontal. \(\ -\frac{5}{9}\)también puede ser una fracción reducida de\(\ \frac{a}{b}\), como en el problema anterior. Por ejemplo, la asíntota se\(\ y=-\frac{10}{18} x\) reduce a\(\ y=-\frac{5}{9} x\).

Si la hipérbola es horizontal, entonces la ecuación de la asíntota es\(\ y=-\frac{b}{a} x\) y eso haría\(\ a=9\)\(\ b=5\) y y la ecuación sería\(\ \frac{x^{2}}{81}-\frac{y^{2}}{25}=1\). Si la ecuación es vertical, entonces la asíntota es\(\ y=-\frac{a}{b} x\) y\(\ a=5\) y\(\ b=9\). La ecuación sería\(\ \frac{y^{2}}{25}-\frac{x^{2}}{81}=1\). Si la pendiente se reduce de una fracción mayor, también podríamos tener\(\ \frac{x^{2}}{324}-\frac{y^{2}}{100}=1\) o\(\ \frac{y^{2}}{100}-\frac{x^{2}}{324}=1\) como posible respuesta.

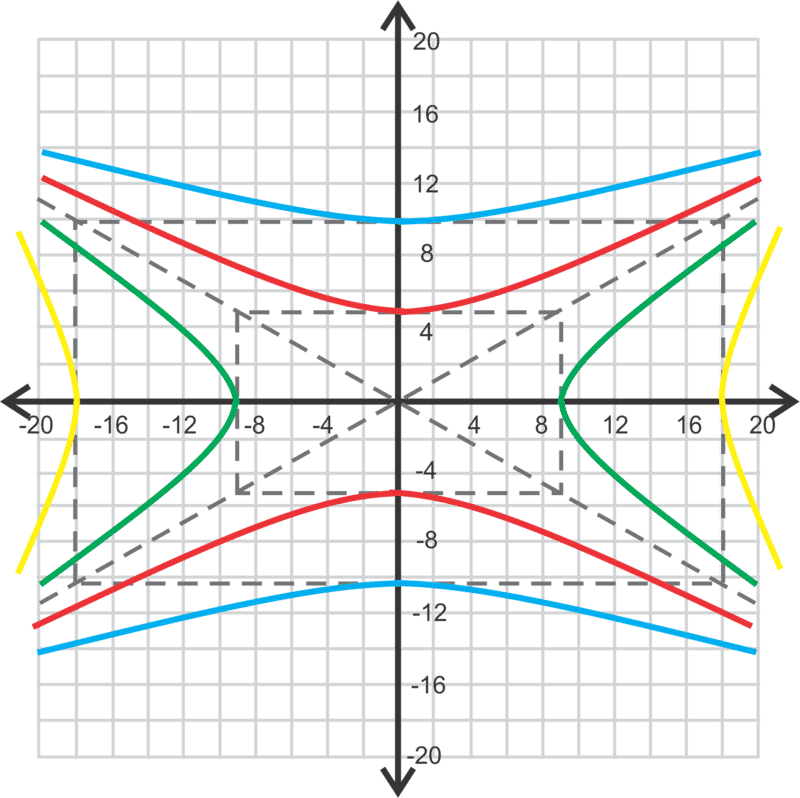
f-d_b2872a6f99a25ed745302d03cd9d6358b7ef838b3936f14be81d7f1e+image_tiny+image_tiny.png

Hay infinitamente muchas ecuaciones hiperbólicas con esta asíntota.

Ejemplos

Ejemplo 1

Antes, se le pidió que encontrara la ecuación de la parábola dado el acertijo.

Solución

Debido a que el vértice y el foco están en el\(\ y \text {-axis }\), sabemos que el eje transversal es vertical.

Por lo tanto, la ecuación será\(\ \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\).

Desde el vértice y el foco, lo sabemos\(\ a=2\) y\(\ c=3\). Vamos a resolver para\(\ b^{2}\) usar\(\ c^{2}=a^{2}+b^{2}\).

\ (\\ comenzar {alineado}
3^ {2} &=2^ {2} +b^ {2}\\
9 &=4+b^ {2}\ fila derecha b^ {2} =5
\ final {alineado}\)

Por lo tanto, la ecuación de la hipérbola será\(\ \frac{y^{2}}{4}-\frac{x^{2}}{5}=1\).

Encuentra la ecuación de las siguientes hipérbolas, centradas en el origen, con la información dada.

Ejemplo 2

vértice: (0, 2)

enfoque: (0, 5)

Solución

El vértice está en el eje y, por lo que esta es una hipérbola vertical con\(\ a=2\). \(\ c=5\), así que tenemos que encontrar\(\ b^{2}\).

\ (\\ begin {array} {l}
c^ {2} &=a^ {2} +b^ {2}\\
25&=4+b^ {2}\ fila derecha b^ {2} =21
\ end {array}\)

La ecuación de la hipérbola es\(\ \frac{y^{2}}{4}-\frac{x^{2}}{21}=1\).

Ejemplo 3

asíntota:\(\ y=x\)

vértice:\(\ (4,0)\)

Solución

Reescribiendo la pendiente de\(\ y=x\), obtenemos\(\ y=\frac{1}{1} x\). Entonces, eso lo sabemos\(\ a\) y\(\ b\) estamos en una proporción de 1:1.

Porque el vértice es\(\ (4,0)\), eso lo sabemos\(\ a=4\) y que la hipérbola es horizontal. Porque\(\ a\) y\(\ b\) están en una proporción de 1:1,\(\ b\) tiene que ser igual a 4 también. La ecuación de la hipérbola es\(\ \frac{x^{2}}{16}-\frac{y^{2}}{16}=1\).

Ejemplo 4

Encuentra las ecuaciones de dos hipérbolas, centradas en el origen, con diferentes\(\ a\) y\(\ b\) valores y una asíntota de\(\ y=\frac{3}{4} x\).

Solución

Una posibilidad es esa\(\ b=3\) y\(\ a=4\) hacer la ecuación\(\ \frac{x^{2}}{16}-\frac{y^{2}}{9}=1\). Una segunda posibilidad podría ser eso\(\ a\) y\(\ b\) son una multiplicación de la relación 4:3. Entonces,\(\ a=8\) y\(\ b=6\), haciendo la ecuación\(\ \frac{x^{2}}{64}-\frac{y^{2}}{36}=1\).

Revisar

Encuentra la ecuación de la hipérbola, centrada en el origen, dada la siguiente información.

vértice:\(\ (−2,0)\), enfoque:\(\ (−5,0)\)
vértice:\(\ (4,0)\), enfoque:\(\ (7,0)\)
\(\ b=8\), enfoque:\(\ (−15,0)\)
vértice:\(\ (−6,0)\), asíntota:\(\ y=\frac{4}{3} x\)
\(\ b=6\), enfoque:\(\ (0,11)\)
vértice:\(\ (0,5)\), asíntota:\(\ y=x\)
asíntota:\(\ y=-\frac{1}{2} x\), vértice:\(\ (6,0)\)
asíntota:\(\ y=3x\),\(\ b=9\), eje transversal vertical
vértice:\(\ (0,8)\), enfoque:\(\ (0,6 \sqrt{2})\)
Encuentra la ecuación de dos hipérbolas de tal manera que tengan lo mismo\(\ a\) y\(\ b\) valores, la ecuación de una asíntota es\(\ y=\frac{4}{5} x\), y centrada en el origen.
Encuentra la ecuación de dos hipérbolas de tal manera que tengan\(\ b\) valores diferentes\(\ a\) y, ambos horizontales, la ecuación de una asíntota es\(\ y=-\frac{2}{3} x\), y centrada en el origen.
Encuentra la ecuación de dos hipérbolas de tal manera que tengan\(\ b\) valores diferentes\(\ a\) y, ambos verticales, la ecuación de una asíntota es\(\ y=6x\), y centrada en el origen.
Encuentra la ecuación de dos hipérbolas de tal manera que tengan lo mismo\(\ a\) y\(\ b\) valores, la ecuación de una asíntota es\(\ y=-\frac{10}{7} x\), y centrada en el origen.