2.5: Límites que involucran funciones radicales
- Page ID
- 105903
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Son muchos los problemas que implicarán tomar la enésima raíz de una expresión variable, por lo que es natural que en ocasiones pueda haber la necesidad de encontrar el límite de una función que involucre expresiones radicales, usando raíces cuadradas o cubitas, u otras raíces. ¿Crees que encontrar el límite de una función que involucra radicales sería diferente a encontrar el límite de funciones polinómicas o racionales? ¿Se te ocurre alguna manera en que los radicales puedan presentar problemas diferentes a los polinomios?
Límites con funciones radicales
Al evaluar un límite que involucre una función radical, use la sustitución directa para ver si un límite puede ser evaluado siempre que sea posible. De no ser así, es necesario explorar otros métodos para evaluar el límite.
Tome la siguiente función
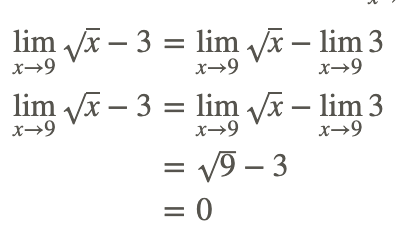
Por lo tanto,
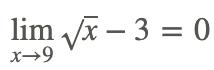
que se pudo haber determinado evaluando directamente f (x) a x=9, es decir, usando sustitución directa.
Ahora, encuentra
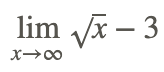
En ambos casos anteriores, se podría utilizar la sustitución directa para evaluar los límites y no hay necesidad de métodos alternativos.
Echa un vistazo a la función
Primero notamos que debemos excluir x=− 5/7 en cualquier evaluación. El uso de la sustitución directa para encontrar el límite da como resultado la forma indeterminada ∞/∞. Para transformar la expresión radical a una mejor forma, utilice el hecho de que el valor de x va a valores positivos cada vez más grandes. Esto permite lo siguiente:
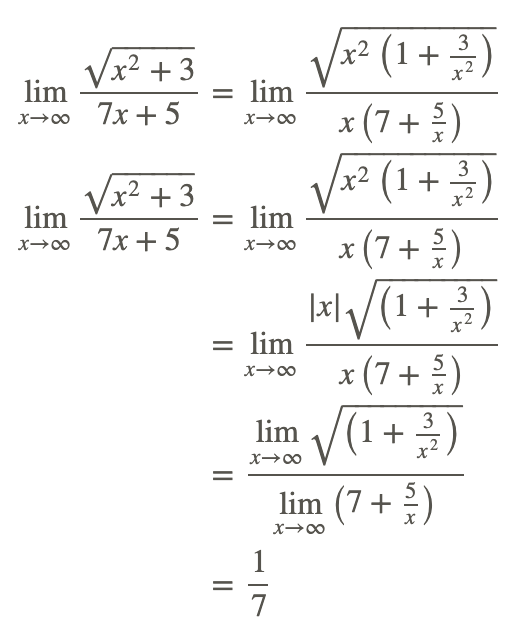
Por lo tanto,
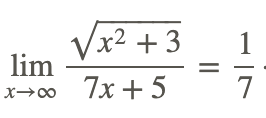
Ahora, encuentra
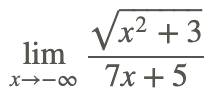
La solución para evaluar el límite al infinito negativo es similar al enfoque anterior excepto que x siempre es negativo.
Por lo tanto.
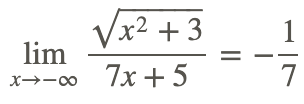
Hasta el momento, has podido encontrar el límite de funciones racionales utilizando métodos mostrados anteriormente. No obstante, hay momentos en los que esto no es posible. Toma la función
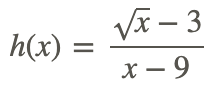
Encuentra
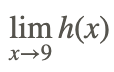
El uso de la sustitución directa para encontrar el límite da como resultado la forma indeterminada 00. Para evaluar el límite, necesitamos transformar la expresión para eliminar la forma indeterminada. Esto se logra usando la relación para la diferencia de cuadrados de números reales: x 2 −y 2 =( x+y) (x−y).
Luego reescribimos y simplificamos la función original de la siguiente manera:
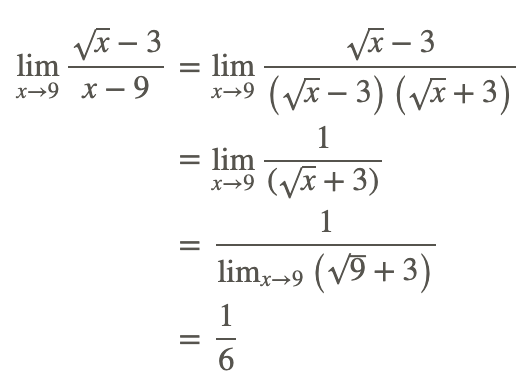
Utilice la diferencia de cuadrados factorización para eliminar el 0 en el denominador.
De ahí
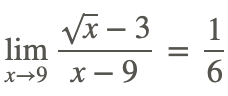
Ahora, encuentra el comportamiento final de la misma función, es decir, encontrar
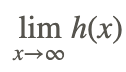
A medida que x aumenta a valores positivos grandes, la función adquiere la forma indeterminada ∞/∞. La transformación anterior también puede ser utilizada para evaluar el límite (Enfoque 1), así como la técnica utilizada en la evaluación de funciones racionales (Enfoque 2).
De ahí
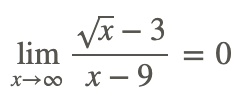
Finalmente, encuentra
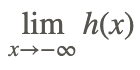
La solución a este problema es que el límite no existe porque el dominio de h (x) no incluye x<0.
Ejemplos
Ejemplo 1
Anteriormente, se le preguntó si los métodos para evaluar límites que involucran polinomios y funciones racionales pueden usarse para encontrar los límites de las funciones radicales. Algunos de los métodos funcionan para funciones radicales. El uso de la sustitución directa es un método común. Transformar formas indeterminadas o indefinidas encontrando y cancelando factores comunes en el numerador y denominador, o factorizando y simplificando las potencias de mayor grado de las variables representan enfoques comunes.
Una de las diferencias notables entre las funciones polinomiales y radicales es que el dominio de los polinomios puede incluir todos los valores reales de la variable independiente, pero el dominio de las funciones radicales, por ejemplo, x√, está restringido.
Ejemplo 2
Encuentra
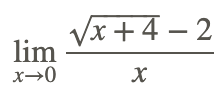
El uso de la sustitución directa para encontrar el límite de la función da como resultado la forma indeterminada 0/0. Para transformar la expresión radical a una mejor forma, haga lo siguiente:
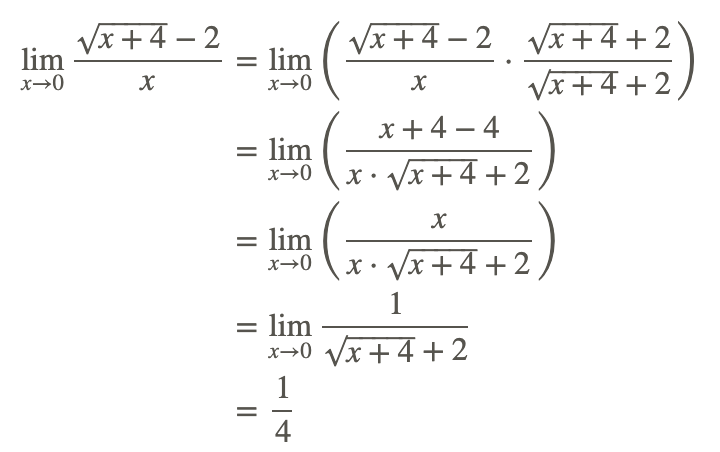
... Racionalizar el numerador: multiplicar por el conjugado del numerador
Por lo tanto,
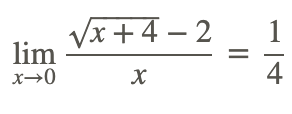
Revisar
Encuentra cada uno de los siguientes límites si existen.
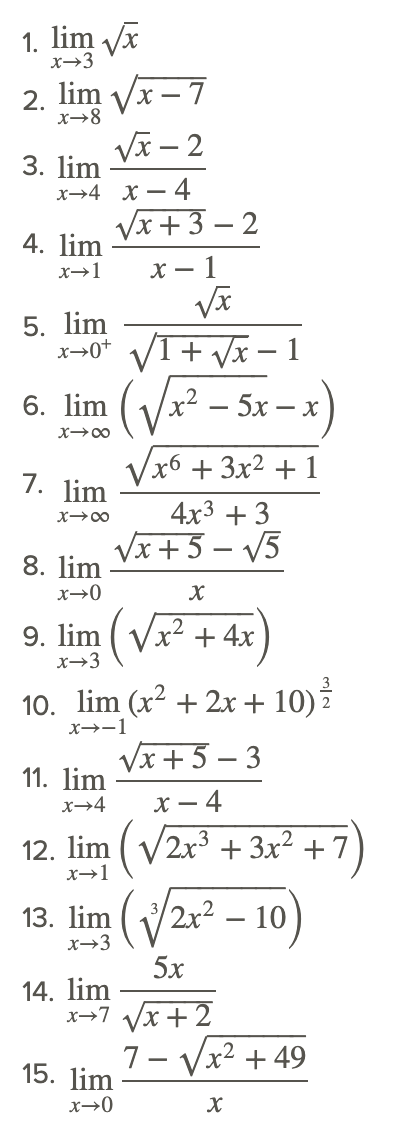
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.6.
El vocabulario
| Término | Definición |
|---|---|
| indeterminado | En matemáticas, una expresión es indeterminada si no se define con precisión. Hay siete formas indeterminadas: 0/0 ,0∞, ∞/∞, ∞ −∞, ∞ −∞, 0 0, ∞ 0, y 1^\ infty. |
| límite | Un límite es el valor que la salida de una función se acerca a medida que la entrada de la función se acerca a un valor dado. |
| función radical | Las funciones radicales son funciones que contienen enésima raíz de expresiones variables. |
Recursos adicionales
Video: Límites en el infinito
Práctica: Límites que involucran funciones radicales
Mundo real: Maverick Surfers