8.2: Método de Newton
- Page ID
- 106019
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Queremos mirar a encontrar las raíces de un polinomio. A veces el polinomio no se puede factorizar fácilmente, y otros métodos algebraicos (por ejemplo, la ecuación cuadrática) no son aplicables, o no funcionan. Ante un problema matemático que no puede resolverse con medios algebraicos simples, el cálculo a veces proporciona una manera de encontrar soluciones aproximadas.
Método de Newton
Un ejemplo sencillo ayudará a introducir el Método de Newton para aproximar las raíces de una ecuación polinómica.
Digamos que quieres calcular\( \sqrt{5} \nonumber\) sin usar una calculadora o una tabla. ¿Alguna idea de cómo se podría hacer esto? Intenta pensar en este problema de una manera diferente, para que hagas uso de la linealización.
Supongamos que estamos interesados en resolver la ecuación cuadrática:
\[ f(x)=x^2−5=0 \nonumber\]
Sabemos que esta ecuación tiene las raíces\( x=± \sqrt{5} \nonumber\).
La idea aquí es encontrar la linealización de f (x) en un punto apropiado, y luego resolver la ecuación lineal para x ¡Esto es un giro agregado al problema de linealización!
¿Cómo elegir el punto de linealización? Ya que\( \sqrt{4}<\sqrt{5}<\sqrt{9} \nonumber\), esto significa\( 2<\sqrt{5}<3 \nonumber\).
Elegimos la aproximación lineal de f (x) para estar cerca\( x_0=2 \nonumber\) (pero, también\( x_0=3 \nonumber\) podría seleccionarse).
\[ f(x)=x^2−5 \mbox{ and } f(2)=−1 \nonumber\]
\[ f′(x)=2x \mbox{ and } f′(2)=4 \nonumber\]
Usando la fórmula de aproximación lineal,
\[ f(x)≈f(x_0)+f′(x_0)(x−x_0) \nonumber\]
\[ ≈−1+(4)(x−2) \nonumber\]
\[ ≈−1+4x−8 \nonumber\]
\[ ≈4x−9 \nonumber\]
Observe que esta ecuación es mucho más fácil de resolver que\( f(x)=x^2−5=0 \nonumber\).
Estableciendo f (x) =0 y resolviendo para x, obtenemos,
\[ 4x−9=0 \nonumber\]
\[ x=\frac{9}{4} \nonumber\]
\[ =2.25 \nonumber\]
Esta es una aproximación bastante buena, ya que una calculadora daría x=2.23607, menor en 0.014. De hecho, podemos hacer esta aproximación a la raíz de f (x) aún mejor repitiendo lo que acabamos de hacer pero usando la última estimación\( x_1=2.25= \frac{9}{4} \nonumber\), un número que está aún más cerca del valor real de\( \sqrt{5} \nonumber\).
\[ f(x)=x^2−5 \mbox{ and } f(2.25)=\frac{1}{16} \nonumber\]
\[ f′(x)=2x \mbox{ and } f′(2)= \frac{9}{2} \nonumber\]
Usando de nuevo la aproximación lineal,
\[ f(x)≈f(x_1)+f′(x_1)(x−x_1) \nonumber\]
\[ ≈ \frac{1}{16}+\frac{9}{2}(x−\frac{9}{4}) \nonumber\]
\[ ≈\frac{9}{2}x−\frac{161}{16} \nonumber\].
Resolviendo para x configurando f (x) =0, obtenemos
\[ x=x_2=\frac{161}{72}=2.23611 \nonumber\]
que es una aproximación aún mejor que\[ x_1=\frac{9}{4} \nonumber\].
Podríamos continuar con este proceso generando una mejor aproximación a\( \sqrt{5} \nonumber\), como se muestra en la tabla, donde la última estimación aproxima la respuesta correcta a 5 lugares. ¡Gracias a Dios por las calculadoras!
|
n |
\( x_n \nonumber\) |
\( f(x_n) \nonumber\) |
\( f′(x-n) \nonumber\) |
\( \frac{f(x_n)}{f′(x_n)} \nonumber\) |
\( x_n−\frac{f(x_n)}{f′(x_n)} \nonumber\) |
|
1 |
2 |
-1 |
4 |
-0.25 |
2.25 |
|
2 |
2.25 |
0.0625 |
4.5 |
0.01389 |
2.23611 |
|
3 |
2.23611 |
0.00019 |
4.47222 |
0.00004 |
2.23607 |
|
4 |
2.23607 |
— |
— |
— |
— |
Esta es la idea básica del Método de Newton. Aquí hay un resumen del método:
- Dada la función f (x), encuentra f′ (x).
- Estimar la primera aproximación, x 0, a una solución de la ecuación f (x) =0. Use una gráfica para ayudar a encontrar la primera aproximación si es necesario (consulte la Figura a continuación).
- Usa la aproximación actual x n para encontrar la siguiente aproximación, x n +1, usando la relación de recursión.
\[ x_{n+1}=x_n−\frac{f(x_n)}{f′(x_n)} \nonumber\].
- Repita el paso anterior hasta que se produzca el nivel deseado de convergencia.
Tenga en cuenta que en algunos casos, el Método de Newton no converge.
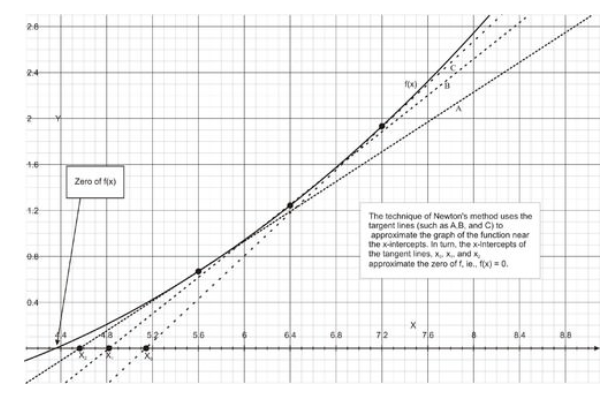
CC BY-NC-SA
Ejemplos
Ejemplo 1
Compare las soluciones con f (x) =5x2+7x−52 en el intervalo [2, 3] de usar la fórmula cuadrática y usando el Método de Newton.
La función se muestra en la figura.
Para f (x) =5x2+7x−52=0, el uso de la fórmula cuadrática da la solución exacta x=2.6 en el intervalo.
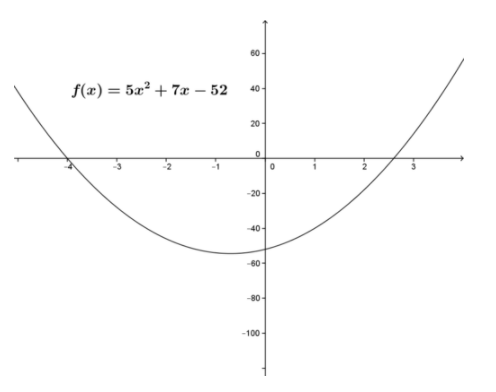
CC BY-NC-SA
El uso del Método de Newton con una estimación inicial de x 0 =3, arroja los resultados mostrados en la tabla.
|
n |
\( x_n \nonumber\) |
\( f(x_n) \nonumber\) |
\( f′(x-n) \nonumber\) |
\( \frac{f(x_n)}{f′(x_n)} \nonumber\) |
\( x_n−\frac{f(x_n)}{f′(x_n)} \nonumber\) |
|
1 |
3 |
14 |
37 |
0.3784 |
2.6216 |
|
2 |
2.6216 |
0.7151 |
33.216 |
0.0215 |
2.6001 |
|
3 |
2.6001 |
0.0033 |
33.001 |
0.0001 |
2.6000 |
|
4 |
2.6000 |
— |
— |
— |
— |
La técnica converge rápidamente en una solución.
Ejemplo 2
Usa el método de Newton para encontrar las raíces del polinomio\( f(x)=x^3+x−1 \nonumber\).
El problema es resolver la ecuación\( f(x)=x^3+x−1=0 \nonumber\).
Las ecuaciones que necesitamos son:
\[ f(x)=x^3+x−1 \nonumber\]
\[ f′(x)=3x^2+1 \nonumber\].
Usando la relación de recursión,
\[ x_{n+1}=x_n−\frac{f(x_n)}{f′(x_n)} \nonumber\]
\[ =x_n−\frac{x^3_n+x_n−1}{3x^2_n+1} \nonumber\].
Para ayudarnos a encontrar la primera aproximación, hacemos una gráfica de f (x). Como sugiere la figura, conjunto\( x_1=0.6 \nonumber\).
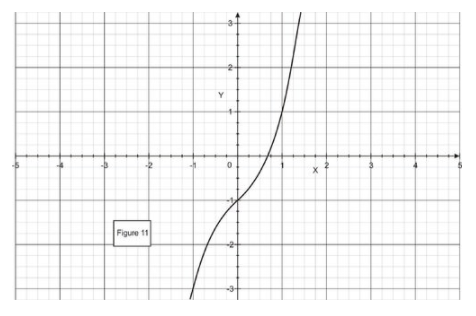
CC BY-NC-SA
Luego usando la relación de recursión, podemos generar x1:
\[ x_{n+1}=x_n−\frac{x^3_n+x_n−1}{3x^2_n+1} \nonumber\]
\[ x_2=0.6−\frac{(0.6)^3+(0.6)−1}{3(0.6)^2+1} \nonumber\]
\[ =0.6884615 \nonumber\].
Al usar la relación de recursión varias veces, podemos encontrar x3 y x4 como se muestra en la tabla.
|
n |
\( x_n \nonumber\) |
\( f(x_n) \nonumber\) |
\( f′(x-n) \nonumber\) |
\( \frac{f(x_n)}{f′(x_n)} \nonumber\) |
\( x_n−\frac{f(x_n)}{f′(x_n)} \nonumber\) |
|
1 |
0.6 |
-0.184 |
2.08 |
-0.0884615 |
0.6884615 |
|
2 |
0.6884615 |
0.01477796 |
2.4219377 |
0.0061017 |
0.6823598 |
|
3 |
0.6823598 |
0.00007669 |
2.3968445 |
0.0000320 |
0.6823278 |
|
4 |
0.6823278 |
— |
— |
— |
— |
Concluimos que la solución a la ecuación\[ x^3+x−1=0 \nonumber\] es de aproximadamente 0.6823.
Ejemplo 3
Utilice el Método de Newton para mostrar para encontrar la raíz de\( f(x)=cos(2x)−x \nonumber\).
Las ecuaciones que necesitamos son:
\( f(x)=cos(2x)−x \nonumber\)
\( f(x)=−2sin(2x)−1 \nonumber\)
Usando la relación de recursión,
x_ {n+1} =x_n\ frac {f (x_n)} {f′ (x_n)}\ nonumber\)
\( =x_n−\frac{cos(2x_n)−x_n}{−2sin(2x_n)−1} \nonumber\)
Para ayudarnos a encontrar la primera aproximación, hacemos una gráfica de f (x). Como sugiere la cifra, establecer la primera estimación en 0.5.
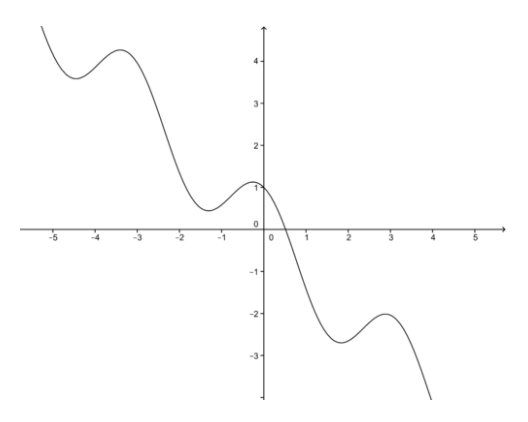
CC BY-NC-SA
El uso de la relación de recursión varias veces da los valores de la tabla:
|
n |
\( x_n \nonumber\) |
\( f(x_n) \nonumber\) |
\( \frac{f(x_n)}{f′(xn)} \nonumber\) |
|
1 |
0.500000 |
0.0403023 |
-0.015216_8 |
|
2 |
0.515022 |
-0.0002400 |
0.0000884 |
|
3 |
0.514933 |
-0.0000000 |
0.0000000 |
|
4 |
0.514933 |
— |
— |
Concluimos que la solución a la ecuación cos (2x) −x=0 es 0.514933.
Revisar
Para todos los problemas, usa el Método de Newton para encontrar las raíces.
- \( x^3+3=0 \nonumber\).
- \( −x+3\sqrt{−1+x}=0 \nonumber\).
- \( 4x^2−x−2 \mbox{ in the interval } [-1, 0] \nonumber\).
- \( 4x^3−6x^2−1 \nonumber\).
- \( 5e^{−x}+x^3 \nonumber\).
- \( cosx−x \nonumber\).
- \( x^5−7x^2+2 \mbox{ in the interval} [-1, 0] \nonumber\).
- \( x^5−7x^2+2 \mbox{ in the interval } [0, 1] \nonumber\).
- \( x^2cosx−x \mbox{ in the interval } [4, 5] \nonumber\).
- \( x^2cosx−x \mbox{ in the interval } [7, 8] \nonumber\).
- \( f(x)=x−2sin(x) \mbox{ to five decimal places, starting with initial guess } x_0=3 \nonumber\).
- \( f(x)=6x^3−4x+1 \nonumber\)a tres decimales, comenzando con la suposición inicial\( x_0=1.2 \nonumber\).
- \( f(x)=ln(x)×(ln(x)+4)+1 \nonumber\)a cinco decimales, comenzando con la suposición inicial\( x_0=1 \nonumber\).
- \( f(x)=tan(x)−csc(x) \nonumber\)a seis dígitos de precisión, comenzando con la suposición inicial\( x_0=0.7 \nonumber\).
- \( f(x)=tan^{−1}(x)+cos(x) \nonumber\)a cuatro dígitos de precisión, comenzando con la suposición inicial\( x_0=−2 \nonumber\).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.11.
El vocabulario
| Término | Definición |
|---|---|
| Método de Newton | El método de Newton es un procedimiento iterativo para calcular la raíz de una ecuación. |
Recursos adicionales
PLIX: Juega, aprende, interactúa, explora - Método de Newton
Video: Método de Newton para resolver ecuaciones
Práctica: Método de Newton
Mundo real: Llegar a la raíz de las cosas

