17.6: Tamaño de la población
- Page ID
- 108970
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)¿Cuántos gansos son el número correcto para esta zona?
¡Tantos como puedan sobrevivir y tener descendencia sana! La figura anterior muestra una bandada de gansos nevados en el Refugio Nacional de Vida Silvestre Kenai. Su población tenderá a crecer lo más grande que pueda por los recursos disponibles. Una vez que sea demasiado grande, algunos de sus miembros morirán. Esto mantiene el tamaño de la población en el número correcto.
Cómo crecen las poblaciones
Una población suele crecer cuando tiene lo que necesita. Si hay mucha comida y otros recursos, la población se hará más grande. Consulte la siguiente tabla (Tabla a continuación); muestra cómo creció una población de bacterias. Se agregó una sola célula bacteriana a un recipiente de nutrientes. Las condiciones fueron ideales. Las bacterias se dividieron cada 30 minutos. ¡Después de apenas 10 horas, había más de un millón de bacterias! Supongamos que la población de bacterias sigue creciendo a este ritmo. ¿Cuántas bacterias habrá a las 10.5 horas? ¿O a las 12 horas?
| Tiempo (horas) | Número de bacterias |
|---|---|
| 0 | 1 |
| 0.5 | 2 |
| 1.0 | 4 |
| 1.5 | 8 |
| 2.0 | 16 |
| 2.5 | 32 |
| 3.0 | 64 |
| 3.5 | 128 |
| 4.0 | 256 |
| 4.5 | 512 |
| 5.0 | 1,024 |
| 5.5 | 2,048 |
| 6.0 | 4,096 |
| 6.5 | 8,192 |
| 7.0 | 16,384 |
| 7.5 | 32,768 |
| 8.0 | 65,536 |
| 8.5 | 131,072 |
| 9.0 | 262,144 |
| 9.5 | 524,288 |
| 10 | 1,048,576 |
Tasa de crecimiento poblacional
La tasa de crecimiento poblacional es la rapidez con la que crece una población. La letra r significa la tasa de crecimiento. La tasa de crecimiento es igual al número de nuevos integrantes agregados a la población en un año por cada 100 miembros que ya están en la población. La tasa de crecimiento incluye nuevos integrantes agregados a la población y antiguos alejados de la población. Los nacimientos agregan nuevos miembros a la población. Las muertes sacan a miembros de la población. La fórmula para la tasa de crecimiento poblacional es:
r = b - d, donde
-
-
- b = tasa de natalidad (número de nacimientos en 1 año por cada 100 miembros de la población)
-
-
-
- d = tasa de mortalidad (número de muertes en 1 año por cada 100 miembros de la población)
-
Si la tasa de natalidad es mayor que la tasa de mortalidad, r es positiva. Esto quiere decir que la población está creciendo. Por ejemplo, si b = 10 y d = 8, r = 2. Esto significa que la población está creciendo en 2 individuos al año por cada 100 miembros de la población. Esto puede no sonar como mucho, pero es una tasa de crecimiento bastante alta. ¡Una población que crece a este ritmo se duplicaría en tan solo 35 años!
Si la tasa de natalidad es menor que la tasa de mortalidad, r es negativa. Esto quiere decir que la población es cada vez más pequeña. ¿Qué crees que podría hacer que esto suceda?
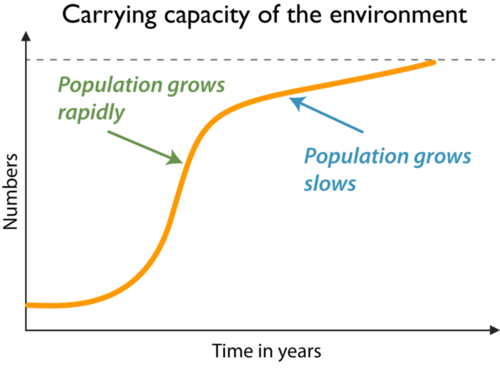
Capacidad de carga
Una población no puede seguir creciendo cada vez más grande para siempre. Tarde o temprano, se le acabarán las cosas que necesita. Para una especie dada, existe una población máxima que puede ser sustentada por el medio ambiente. Este máximo se llama la capacidad de carga. Cuando una población se acerca a la capacidad de carga, suele crecer más lentamente (Figura a continuación). Cuando la población alcanza la capacidad de carga, deja de crecer.
Una población no puede llegar a ser mucho mayor que la capacidad de carga. ¿Qué podría pasar si lo hiciera?
Resumen
- Una población crecerá siempre y cuando tenga lo que necesita.
- La capacidad de carga de un ambiente se alcanza cuando el número de nacimientos es igual al número de defunciones.
- Un factor limitante determina la capacidad de carga de una especie.
Revisar
- ¿Qué sucede si una población supera su capacidad de carga?
- Explique cómo una sola bacteria puede crecer hasta llegar a una población de más de un millón 10 horas después.
- ¿Qué sucede si la tasa de natalidad en una población es mayor que la tasa de mortalidad? ¿Qué pasa si es menor?