1.4: Midpoints y Segmento Bisectriz
- Page ID
- 107622
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Usa puntos medios y bisectores para encontrar la marca a mitad de camino entre dos coordenadas.
Cuando dos segmentos son congruentes, indicamos que son congruentes, o de igual longitud, con marcas de segmento, como se muestra a continuación:
Figura\(\PageIndex{1}\)Un punto medio es un punto en un segmento de línea que lo divide en dos segmentos congruentes.
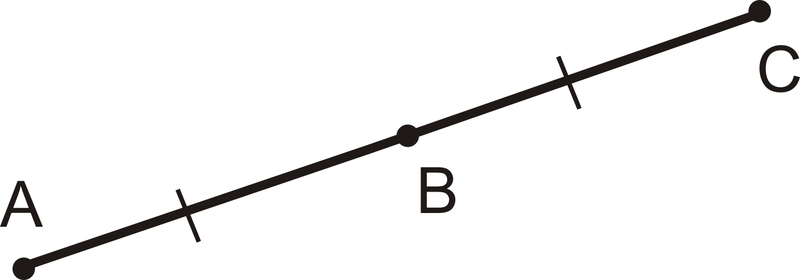Figura\(\PageIndex{2}\)Porque\(AB=BC\),\(B\) es el punto medio de\(\overline{AC}\). Cualquier segmento de línea tendrá exactamente un punto medio.
Cuando se trazan puntos en el plano de coordenadas, podemos usar una fórmula para encontrar el punto medio entre ellos.
Aquí hay dos puntos,\((-5, 6)\) y\((3, 2).\)
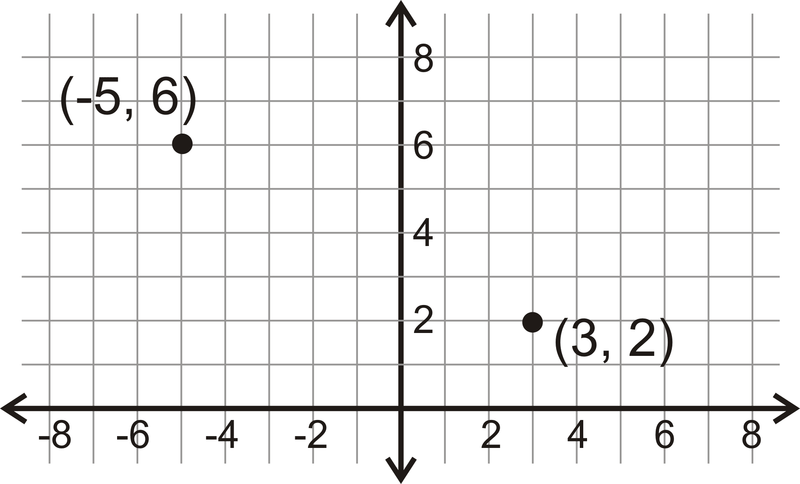Figura\(\PageIndex{3}\)El punto medio debe estar a medio camino entre los puntos del segmento que los conecta. Con solo mirar, parece que el punto medio es\((-1, 4).\)
Fórmula de punto medio: Para dos puntos, (\(x_1, y_1\)) y (\(x_2,y_2\)), el punto medio es\(\left (\dfrac{x_1+x_2}{2} , \dfrac{y_1+y_2}{2}\right) \).
Usemos la fórmula para asegurarnos de que\((-1, 4)\) es el punto medio entre\((-5, 6)\) y\((3, 2)\).
\(\left (\dfrac{-5+3}{2} ,\dfrac{6+2}{2}\right) =(−22,82)=(−1,4) \)
Un segmento bisectriz corta un segmento de línea en dos partes congruentes y pasa a través del punto medio. Una bisectriz perpendicular es una bisectriz de segmento que se cruza con el segmento en ángulo recto.
\(\overline{AB} \cong \overline{BC}\)
\(\overline{AC} \perp \overleftrightarrow{DE}\)
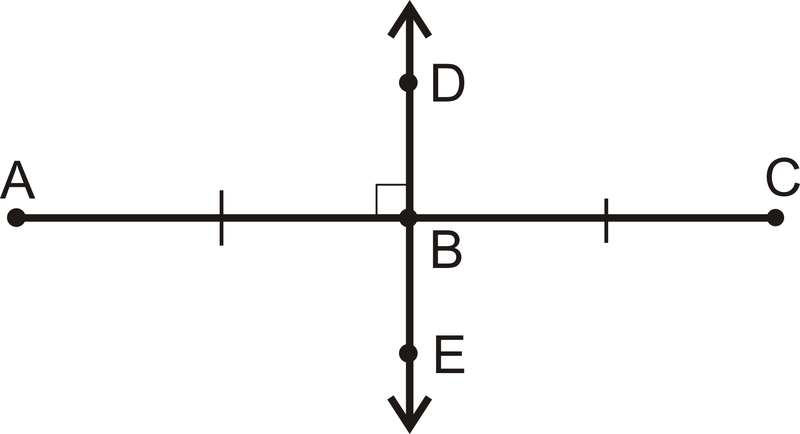Figura\(\PageIndex{4}\)¿Y si te dieran las coordenadas de dos puntos y quisieras encontrar el punto exactamente en medio de ellos? ¿Cómo encontrarías las coordenadas de este tercer punto?
Ejemplo\(\PageIndex{1}\)
Escribir todas las declaraciones de igual segmento.
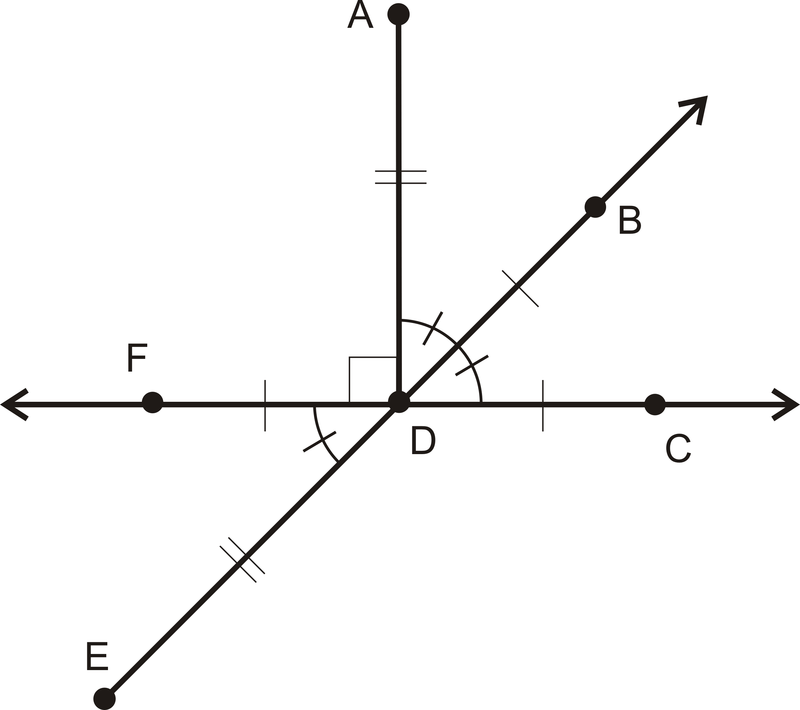Figura\(\PageIndex{5}\)Solución
\(AD=DE\)
\(FD=DB=DC\)
Ejemplo\(\PageIndex{2}\)
Es\(M\) un punto medio de\(\overline{AB}\)?
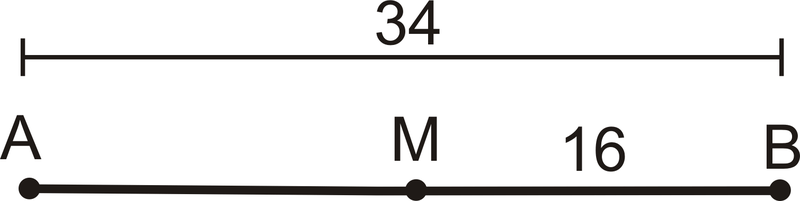
Solución
No, no lo es\(MB=16\) y\(AM=34−16=18\). \(AM\)debe ser igual\(MB\) para que M sea el punto medio de\(\overline{AB}\).
Ejemplo\(\PageIndex{3}\)
Encuentra el punto medio entre\((9, -2)\) y\((-5, 14)\).
Solución
Enchufa los puntos a la fórmula.
\(\left(\dfrac{9+(−5)}{2}\ ,\dfrac{−2+14}{2}\right)=\left(\dfrac{4}{2},\dfrac{12}{2}\right)=(2,6)\)
Ejemplo\(\PageIndex{4}\)
¿De qué línea es la bisectriz perpendicular\(\overline{MN}\)?
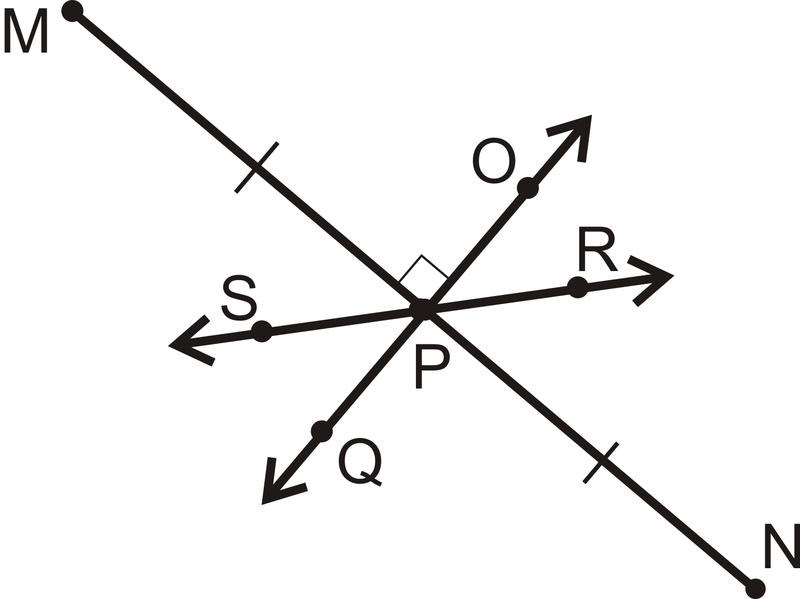Figura\(\PageIndex{7}\)Solución
La bisectriz perpendicular debe biseccionar\(\overline{MN}\) y ser perpendicular a ella. Solo\(\overleftrightarrow{OQ}\) se ajusta a esta descripción. \(\overleftrightarrow{SR}\)es una bisectriz, pero no es perpendicular.
Ejemplo\(\PageIndex{5}\)
Encontrar\(x\) y\(y\).
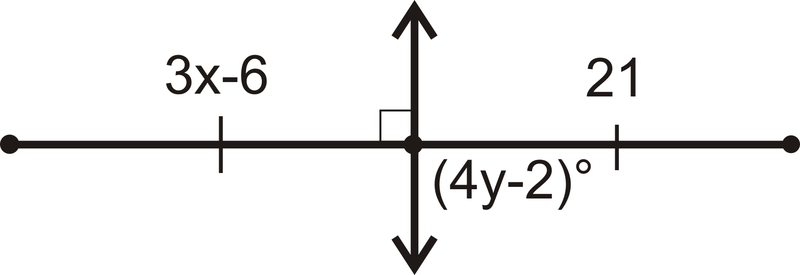Figura\(\PageIndex{8}\)Solución
La línea que se muestra es la bisectriz perpendicular.
Entonces,\(3x−6=21\)
\(3x=27\)
\(x=9\)
Y,\((4y−2)=90\)
\(4y=92\)
\(y=23\)
Revisar
- Copia la figura a continuación y etiquétalas con la siguiente información:
\(\overline{AB} \cong \overline{AD}\)
\(\overline{CD} \cong \overline{BC}\)
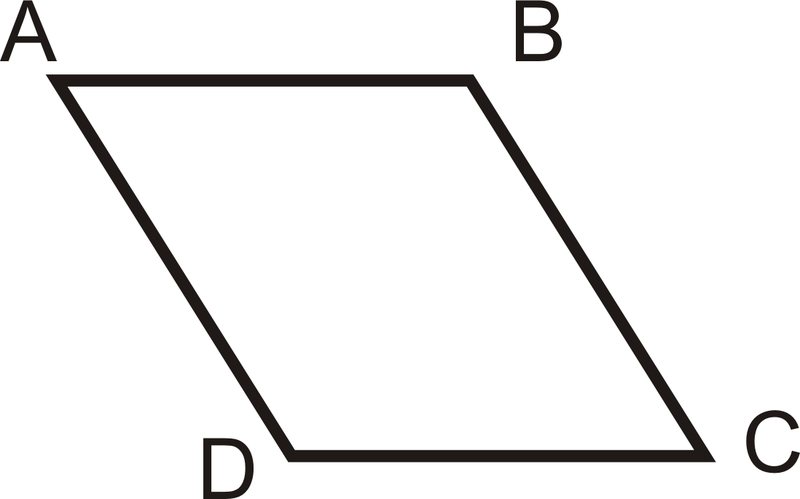Figura\(\PageIndex{9}\)Para 2-4, use la siguiente imagen para responder a las preguntas.
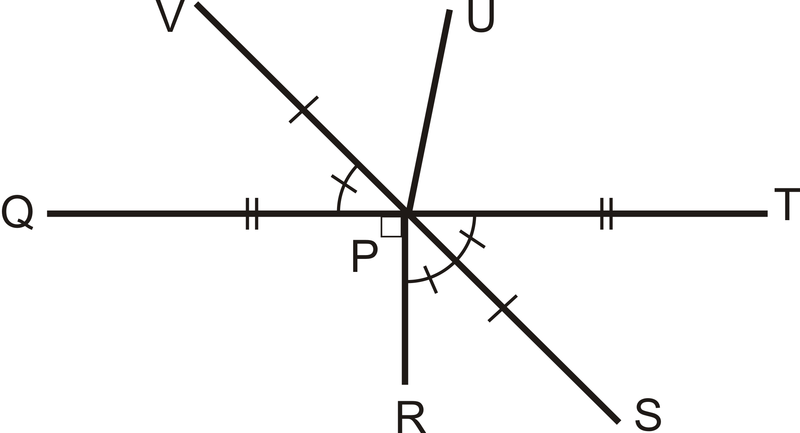Figura\(\PageIndex{10}\)- \(P\)es el punto medio de lo que dos segmentos?
- ¿Cómo\(\overline{VS}\) se relaciona con\(\overline{QT}\)?
- ¿Cómo\(\overline{QT}\) se relaciona con\(\overline{VS}\)?
Para el ejercicio 5, use álgebra para determinar el valor de\(x\).
-
Figura\(\PageIndex{11}\)
Para las preguntas 6-10, encuentra el punto medio entre cada par de puntos.
- (-2, -3) y (8, -7)
- (9, -1) y (-6, -11)
- (-4, 10) y (14, 0)
- (0, -5) y (-9, 9)
- (-3, -5) y (2, 1)
Dado el punto medio (\(M\)) y cualquiera de los extremos de\(\overline{AB}\), encuentre el otro punto final.
- \(A(−1,2)\)y\(M(3,6)\)
- \(B(−10,−7)\)y\(M(−2,1)\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.4.
vocabulario
| Término | Definición |
|---|---|
| punto medio | El punto medio de un segmento de línea es el punto del segmento de línea que divide el segmento en dos partes congruentes. |
| bisectorial perpendicular | Un segmento bisectriz que intersecta el segmento en ángulo recto. |
| segmento bisectorial | Un segmento bisectriz es una línea (o parte de una línea) que pasa por el punto medio. |
| marcas de segmento | Cuando dos segmentos son congruentes, indicamos que son congruentes con marcas de segmento. |
| Fórmula de punto medio | La fórmula del punto medio dice que para los puntos finales\((x_1, y_1)\) y\((x_2, y_2)\), el punto medio es\( \left (\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\right)\). |
Recursos adicionales
Elemento Interactivo
Video: Ejemplos de puntos medios y bisectores de segmentos - Básico
Actividades: Preguntas de discusión sobre puntos medios y bisectores de segmentos
Ayudas de estudio: Guía de estudio de segmentos
Práctica: Puntos medios y bisectores de segmento
Mundo Real: Bisectores de Punto Medio y Segmento - Actividad de Búsqueda del Tesoro