1.10: Clasificación de ángulos
- Page ID
- 107579
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Clasificación de ángulo
Figura\(\PageIndex{1}\)Mark quiere pintar la puerta de su habitación. Las formas en la puerta le recuerdan a la geometría. Decide usar una regla para medir las longitudes reales de los lados y un trasportador para medir los ángulos. Se da cuenta del mismo ángulo repitiéndose una y otra vez. ¿Qué tipo de ángulo está formado por la esquina de la puerta?
En este concepto, aprenderás a clasificar los ángulos.
Clasificación de ángulos
Un ángulo es el espacio creado entre dos líneas, segmentos de línea o rayos conectados en un punto común.
Los ángulos se pueden representar mediante el uso de un símbolo. Aquí está el símbolo de un ángulo.
\(\angle A\)
Esto significa “Ángulo A”.
Los ángulos se miden en grados . Los grados miden la distancia entre las dos líneas. El símbolo o significa “grados”. El número de grados indica qué tan abierto o cerrado está el ángulo. Cuanto menor sea el número de grados, menor o más cerró el ángulo.
Los ángulos se clasifican por su tamaño. Los tamaños de ángulo pueden variar de\(0^{\circ}\) a\(360^{\circ}\), un círculo completo.
Aquí hay un diagrama que muestra algunas medidas de ángulo.
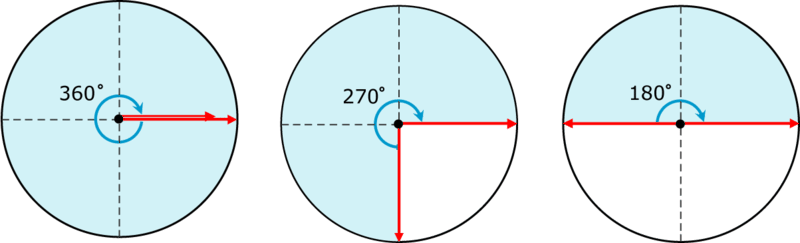Figura\(\PageIndex{2}\)Como puedes ver, un ángulo de\(360^{\circ}\) hace un círculo completo. Un ángulo de\(270^{\circ}\) es tres cuartas partes de un círculo, y un ángulo de\(180^{\circ}\) es medio círculo. Un\(180^{\circ}\) ángulo es una línea recta.
Los ángulos que miden entre 0o y\(180^{\circ}\) se clasifican como agudos, rectos, obtusos o rectos.
Un ángulo agudo mide menos de\(90^{\circ}\).
Un ángulo obtuso tiene una medida mayor que\(90^{\circ}\) y menor que\(180^{\circ}\).
Aquí hay algunos ejemplos.
Figura\(\PageIndex{3}\)La mayoría de los ángulos en el\(180^{\circ}\) rango\(0^{\circ}\) y son agudos u obtusos. Sin embargo, hay dos ángulos especiales con medidas exactas.
Un ángulo recto mide exactamente \(90^{\circ}\). Los ángulos rectos son uno de los conceptos más importantes que debes conocer sobre la geometría. Los ángulos rectos se encuentran en cuadrados, rectángulos y triángulos. También están en todas partes en el mundo real.
Aquí hay algunos ejemplos.
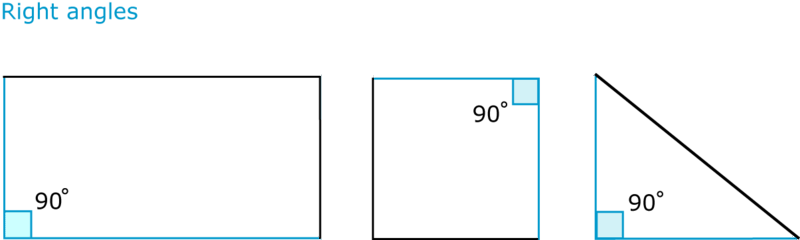Figura\(\PageIndex{4}\)Observe que se usa una caja pequeña cuando un ángulo es un ángulo recto.
Hay muchos lugares en el mundo real donde se puede ver ángulos agudos, obtusos y rectos.
Aquí hay algunos ejemplos.
Figura\(\PageIndex{5}\)Si miras cada una de estas imágenes, puedes ver claramente los ángulos rectos. También observe que los cables del puente se estiran para crear ángulos agudos en cada lado de la viga central.
El otro ángulo especial se llama ángulo recto. Un ángulo recto forma una línea y mide exactamente 180°.
Veamos un ejemplo.
Figura\(\PageIndex{6}\)Ahora, intentemos clasificar los ángulos.
Clasifica cada ángulo a continuación.
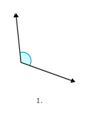Figura\(\PageIndex{7}\)Para cada ángulo, puede ser útil preguntarse: “¿Es más grande o más pequeño que un ángulo recto?”
Recuerde, los ángulos rectos siempre miden\(90^{\circ}\), y se utilizan para decir si un ángulo es agudo u obtuso.
Primero, entienda que el ángulo en la Figura no\(\PageIndex{2}\) es un ángulo recto ni un ángulo recto.
El ángulo no tiene una esquina perfecta para representar un ángulo recto y el ángulo no es una línea recta.
A continuación, determine si el ángulo en la Figura\(\PageIndex{2}\) es mayor o menor que un ángulo recto.
El ángulo es mayor que una esquina perfecta, por lo tanto, el ángulo es mayor que un ángulo recto.
Después, clasifique el ángulo.
Obtuso.
La respuesta es que la Figura\(\PageIndex{2}\) muestra un ángulo obtuso.
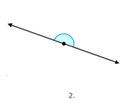Figura\(\PageIndex{8}\)El ángulo en la Figura\(\PageIndex{3}\) parece ser una línea recta.
Primero, reconozca que la Figura\(\PageIndex{3}\) parece ser una línea recta.
La línea no parece doblarse.
A continuación, recuerda el significado de una línea recta.
Una línea recta es un ángulo especial.
Después, clasifique el ángulo.
Recta.
La respuesta es que la Figura\(\PageIndex{3}\) muestra un ángulo recto.
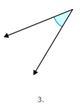
Figura\(\PageIndex{9}\)¿La figura es\(\PageIndex{4}\) más grande o más pequeña que un ángulo recto?
Primero, entienda que el ángulo en la Figura no\(\PageIndex{4}\) es un ángulo recto ni un ángulo recto.
El ángulo no tiene una esquina perfecta para representar un ángulo recto y el ángulo no es una línea recta.
A continuación, determine si el ángulo en la Figura\(\PageIndex{4}\) es mayor o menor que un ángulo recto.
El ángulo es menor que un ángulo recto.
Después, clasifique el ángulo.
Agudo.
La respuesta es que la Figura\(\PageIndex{4}\) muestra un ángulo agudo.
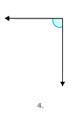
Figura\(\PageIndex{10}\)El ángulo en la Figura\(\PageIndex{5}\) parece ser un tipo especial de ángulo.
Primero, reconocer la apariencia del ángulo en la Figura\(\PageIndex{5}\).
El ángulo parece formar una esquina perfecta.
A continuación, recuerda lo que representa un rincón perfecto.
Un rincón perfecto representa un ángulo especial.
Después, clasifique el ángulo.
Derecha.
La respuesta es que la Figura\(\PageIndex{5}\) muestra un ángulo recto.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Mark y la puerta de su habitación.
Se da cuenta del mismo ángulo en múltiples lugares diferentes de la puerta. ¿Qué tipo de ángulo está formado por la esquina de la puerta?
Solución
En primer lugar, resaltar los ángulos relevantes.
Resalta cada ángulo de esquina.
A continuación, enumere las opciones de ángulo.
Agudo, derecho, obtuso.
Después, etiquetar el ángulo de esquina.
Derecha.
La respuesta es que las esquinas de la puerta son ángulos rectos.
Ejemplo\(\PageIndex{2}\)
Verdadero o falso. Un ángulo agudo también puede ser un ángulo recto.
Solución
En primer lugar, recordar la definición de ángulo agudo.
Un ángulo agudo es menor que\(90^{\circ}\).
A continuación, recuerde que los ángulos que miden exactamente\(90^{\circ}\) son ángulos especiales.
Los ángulos que\(90^{\circ}\) miden exactamente se clasifican como ángulos rectos.
Entonces, exponga su conclusión.
Un ángulo agudo no puede ser un ángulo recto.
La respuesta es que la afirmación es falsa. Un ángulo agudo mide menos que\(90^{\circ}\) mientras que un ángulo recto mide exactamente\(90^{\circ}\), por lo tanto, un ángulo agudo no puede ser un ángulo recto.
Ejemplo\(\PageIndex{3}\)
Identificar cada tipo de ángulo descrito.
Un ángulo mayor que\(90^{\circ}\) pero menor que\(180^{\circ}\).
Solución
Primero, anote el tamaño del ángulo.
El ángulo es mayor que\(90^{\circ}\) pero menor que\(180^{\circ}\).
A continuación, recuerda las reglas para los ángulos.
Hay un nombre para ángulos mayores que\(90^{\circ}\) pero menores que\(180^{\circ}\).
Después, clasifique el ángulo.
Obtuso.
La respuesta es que el ángulo es obtuso.
Ejemplo\(\PageIndex{4}\)
Identificar cada tipo de ángulo descrito.
Un ángulo que mide\(15^{\circ}\).
Solución
Primero, anote el tamaño del ángulo.
El ángulo es menor que\(90^{\circ}\).
A continuación, recuerda las reglas para los ángulos.
Hay un nombre para ángulos que son menores que\(90^{\circ}\).
Después, clasifique el ángulo.
Agudo.
La respuesta es que el ángulo es agudo.
Ejemplo\(\PageIndex{5}\)
Identificar cada tipo de ángulo descrito.
Un ángulo que mide exactamente\(90^{\circ}\)
Solución
Primero, anote el tamaño del ángulo.
El ángulo es exactamente\(90^{\circ}\).
A continuación, recuerda las reglas para los ángulos.
Hay un nombre para ángulos que son exactamente\(90^{\circ}\).
Después clasifique el ángulo.
Derecha.
La respuesta es que el ángulo es un ángulo recto.
Revisar
Etiquete cada ángulo como agudo, obtuso, derecho o recto.
Figura\(\PageIndex{11}\)- \(55^{\circ}\)
- \(102^{\circ}\)
- \(90^{\circ}\)
- \(180^{\circ}\)
- \(10^{\circ}\)
- \(87^{\circ}\)
- \(134^{\circ}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.1.
Recursos
Recurso Adicional
Elemento Interactivo
Video:Animación de Tipos de Ángulos
Actividades: Clasificación de ángulos Preguntas de discusión
Ayudas de estudio: Guía de estudio de ángulos
Práctica: Clasificar ángulos
Mundos reales: Clasificación de ángulos