2.8: Tablas de la Verdad
- Page ID
- 107403
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Hasta ahora conocemos estos símbolos para la lógica:
- \(\sim\)no (negación)
- \(\rightarrow\)si-entonces
- \(\therefore\)por lo tanto
Dos símbolos más son:
- \(\wedge\)y
- \(\lor\)o
Escribiríamos “\(p\)y\(q\)” como\(p\wedge q\) y “\(p\)o\(q\)” como\(p\lor q\).
Las tablas de verdad utilizan estos símbolos y son otra forma de analizar la lógica. Primero, relacionemos p y\ sim p. para que sea más fácil, establezca p como: Un número par. Por lo tanto,\ sim p es Un número impar. Haz una tabla de la verdad para saber si ambos son verdaderos. Empezar con todas las “verdades” de p, verdadero (T) o falso (F).
| p | |
|---|---|
| T | |
| F |
A continuación escribimos los valores de verdad correspondientes para\(\sim p\). \(\sim p\)tiene los valores de verdad opuestos de\(p\). Entonces, si\(p\) es cierto, entonces\(\sim p\) es falso y viceversa.
| p | \ sim |
|---|---|
| T | F |
| F | T |
Para recapitular:
- Inicia tablas de verdad con todas las combinaciones posibles de verdades. Para 2 variables hay 4 combinaciones para 3 variables hay 8. Siempre comienzas una tabla de la verdad de esta manera.
- Hacer cualquier negación sobre cualquiera de las variables.
- Haga cualquier combinación entre paréntesis.
- Terminar con completar lo que el problema estaba pidiendo.
Dibujando una Mesa de Verdad
1. Dibuja una mesa de verdad para\(p\),\(q\) y\(p \wedge q\).
Primero, haz columnas para p y q. Llena las columnas con todas las posibles combinaciones true y false para las dos.
| p | q | |
|---|---|---|
| T | T | |
| T | F | |
| F | T | |
| F | F |
Observe todas las combinaciones de p y q. Siempre que tengamos tablas de verdad con dos variables, así es siempre como llenamos las dos primeras columnas.
A continuación, necesitamos averiguar cuándo\(p\wedge q\) es verdadero, basado en las dos primeras columnas. p\ wedge q solo puede ser verdadero si AMBOS p y q son verdaderos. Entonces, la tabla terminada se ve así:
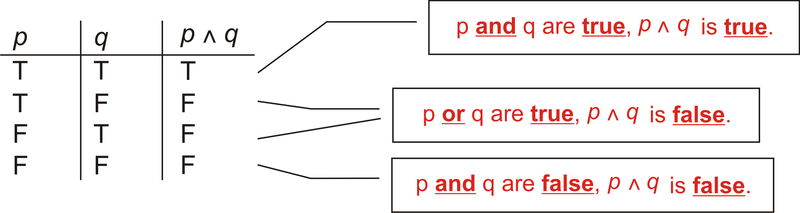Figura\(\PageIndex{1}\)Es así como siempre se llena una tabla de verdad con dos variables y su columna “y”.
2. Dibuja una mesa de verdad para\(p\),\(q\) y\(p \lor q\).
Primero, hacer columnas para\(p \lor q\) y\(q\), al igual que el Ejemplo A.
| p | q | |
|---|---|---|
| T | T | |
| T | F | |
| F | T | |
| F | F |
A continuación, tenemos que averiguar cuándo\(p \lor q\) es verdad, con base en las dos primeras columnas. \(p \lor q\)es cierto si\(p\) OR\(q\) son verdaderas, o ambas son verdaderas. Entonces, la tabla terminada se ve así:
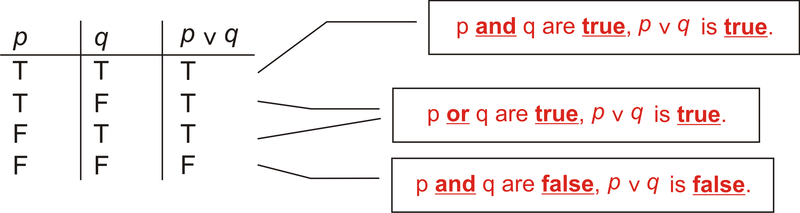Figura\(\PageIndex{2}\)La diferencia entre\(p \wedge q\) y\(p \lor q\) es la segunda y tercera fila. Para “y” ambos\(p\) y\(q\) tienen que ser verdad, pero para “o” sólo uno tiene que ser verdad.
Determinar las verdades de las variables
Determinar las verdades para\(p \wedge(\sim q \lor r)\).
Primero, hay tres variables, así que vamos a necesitar todas las combinaciones de sus verdades. Para tres variables, siempre hay 8 combinaciones posibles.
| \(p\) | \(q\) | \(r\) | |||
|---|---|---|---|---|---|
| \ (p\) ">T | \ (q\) ">T | \ (r\) ">T | |||
| \ (p\) ">T | \ (q\) ">T | \ (r\) ">F | |||
| \ (p\) ">T | \ (q\) ">F | \ (r\) ">T | |||
| \ (p\) ">T | \ (q\) ">F | \ (r\) ">F | |||
| \ (p\) ">F | \ (q\) ">T | \ (r\) ">T | |||
| \ (p\) ">F | \ (q\) ">T | \ (r\) ">F | |||
| \ (p\) ">F | \ (q\) ">F | \ (r\) ">T | |||
| \ (p\) ">F | \ (q\) ">F | \ (r\) ">F |
A continuación, dirija el\(\sim q\). Simplemente serán los opuestos de la\(q\) columna.
| \(p\) | \(q\) | \(r\) | \(\sim q\) | ||
|---|---|---|---|---|---|
| \ (p\) ">T | \ (q\) ">T | \ (r\) ">T | \ (\ sim q\) ">F | ||
| \ (p\) ">T | \ (q\) ">T | \ (r\) ">F | \ (\ sim q\) ">F | ||
| \ (p\) ">T | \ (q\) ">F | \ (r\) ">T | \ (\ sim q\) ">T | ||
| \ (p\) ">T | \ (q\) ">F | \ (r\) ">F | \ (\ sim q\) ">T | ||
| \ (p\) ">F | \ (q\) ">T | \ (r\) ">T | \ (\ sim q\) ">F | ||
| \ (p\) ">F | \ (q\) ">T | \ (r\) ">F | \ (\ sim q\) ">F | ||
| \ (p\) ">F | \ (q\) ">F | \ (r\) ">T | \ (\ sim q\) ">T | ||
| \ (p\) ">F | \ (q\) ">F | \ (r\) ">F | \ (\ sim q\) ">T |
Ahora, hagamos lo que hay entre paréntesis,\(\sim q\lor r\). Recuerda, porque “o” solo\(\sim q\) OR\(r\) tiene que ser verdad. Utilice únicamente las\(r\) columnas\(\sim q\) y para determinar los valores de esta columna.
| \(p\) | \(q\) | \(r\) | \(\sim q\) | \(\sim q\lor r\) | |
|---|---|---|---|---|---|
| \ (p\) ">T | \ (q\) ">T | \ (r\) ">T | \ (\ sim q\) ">F | \ (\ sim q\ lor r\) ">T | |
| \ (p\) ">T | \ (q\) ">T | \ (r\) ">F | \ (\ sim q\) ">F | \ (\ sim q\ lor r\) ">F | |
| \ (p\) ">T | \ (q\) ">F | \ (r\) ">T | \ (\ sim q\) ">T | \ (\ sim q\ lor r\) ">T | |
| \ (p\) ">T | \ (q\) ">F | \ (r\) ">F | \ (\ sim q\) ">T | \ (\ sim q\ lor r\) ">T | |
| \ (p\) ">F | \ (q\) ">T | \ (r\) ">T | \ (\ sim q\) ">F | \ (\ sim q\ lor r\) ">T | |
| \ (p\) ">F | \ (q\) ">T | \ (r\) ">F | \ (\ sim q\) ">F | \ (\ sim q\ lor r\) ">F | |
| \ (p\) ">F | \ (q\) ">F | \ (r\) ">T | \ (\ sim q\) ">T | \ (\ sim q\ lor r\) ">T | |
| \ (p\) ">F | \ (q\) ">F | \ (r\) ">F | \ (\ sim q\) ">T | \ (\ sim q\ lor r\) ">T |
Por último, podemos abordar todo el problema,\(p \wedge(\sim q \lor r)\). Utilice el\(p\) y\(\sim q\lor r\) para determinar los valores. Recuerda, para “y” ambos\(p\) y\(\sim q\lor r\) debe ser cierto.
| \(p\) | \(q\) | \(r\) | \(\sim q\) | \(\sim q\lor r\) | \(p \wedge(\sim q \lor r)\) |
|---|---|---|---|---|---|
| \ (p\) ">T | \ (q\) ">T | \ (r\) ">T | \ (\ sim q\) ">F | \ (\ sim q\ lor r\) ">T | \ (p\ cuña (\ sim q\ lor r)\) ">T |
| \ (p\) ">T | \ (q\) ">T | \ (r\) ">F | \ (\ sim q\) ">F | \ (\ sim q\ lor r\) ">F | \ (p\ cuña (\ sim q\ lor r)\) ">F |
| \ (p\) ">T | \ (q\) ">F | \ (r\) ">T | \ (\ sim q\) ">T | \ (\ sim q\ lor r\) ">T | \ (p\ cuña (\ sim q\ lor r)\) ">T |
| \ (p\) ">T | \ (q\) ">F | \ (r\) ">F | \ (\ sim q\) ">T | \ (\ sim q\ lor r\) ">T | \ (p\ cuña (\ sim q\ lor r)\) ">T |
| \ (p\) ">F | \ (q\) ">T | \ (r\) ">T | \ (\ sim q\) ">F | \ (\ sim q\ lor r\) ">T | \ (p\ cuña (\ sim q\ lor r)\) ">F |
| \ (p\) ">F | \ (q\) ">T | \ (r\) ">F | \ (\ sim q\) ">F | \ (\ sim q\ lor r\) ">F | \ (p\ cuña (\ sim q\ lor r)\) ">F |
| \ (p\) ">F | \ (q\) ">F | \ (r\) ">T | \ (\ sim q\) ">T | \ (\ sim q\ lor r\) ">T | \ (p\ cuña (\ sim q\ lor r)\) ">F |
| \ (p\) ">F | \ (q\) ">F | \ (r\) ">F | \ (\ sim q\) ">T | \ (\ sim q\ lor r\) ">T | \ (p\ cuña (\ sim q\ lor r)\) ">F |
Escribe una tabla de verdad para las siguientes variables.
Ejemplo\(\PageIndex{1}\)
\(p \wedge \sim p\)
Solución
Primero, haga columnas para\(p\), luego agregue\(\sim p\) y finalmente, evalúe\(p \wedge \sim p\).
| \(p\) | \(\sim p\) | \(p \wedge \sim p\) |
|---|---|---|
| \ (p\) ">T | \ (\ sim p\) ">F | \ (p\ cuña\ sim p\) ">F |
| \ (p\) ">F | \ (\ sim p\) ">T | \ (p\ cuña\ sim p\) ">F |
Ejemplo\(\PageIndex{2}\)
\(\sim p \lor \sim q\)
Solución
Primero, haga columnas para\(p\) y\(q\), luego agregue\(\sim p\) y\(\sim q\). Por último, evaluar\(\sim p \lor \sim q\).
| \(p\) | \(q\) | \(\sim p\) | \(\sim q\) | \(\sim p \lor \sim q\) |
|---|---|---|---|---|
| \ (p\) ">\(p \lor \sim q\) | \ (q\) ">T | \ (\ sim p\) ">F | \ (\ sim q\) ">F | \ (\ sim p\ lor\ sim q\) ">F |
| \ (p\) ">T | \ (q\) ">F | \ (\ sim p\) ">F | \ (\ sim q\) ">T | \ (\ sim p\ lor\ sim q\) ">T |
| \ (p\) ">F | \ (q\) ">T | \ (\ sim p\) ">T | \ (\ sim q\) ">F | \ (\ sim p\ lor\ sim q\) ">T |
| \ (p\) ">F | \ (q\) ">F | \ (\ sim p\) ">T | \ (\ sim q\) ">T | \ (\ sim p\ lor\ sim q\) ">T |
Ejemplo\(\PageIndex{3}\)
\(p \wedge (q\lor \sim q)\)
Solución
Primero, haz columnas para p y q, luego agrega\(\sim q\) y\(q\lor \sim q\). Por último, evaluar\(p\wedge (q\lor \sim q)\).
| \(p\) | \(q\) | \(\sim q\) | \(q\lor \sim q\) | \(p\wedge (q\lor \sim q)\) |
|---|---|---|---|---|
| \ (p\) ">T | \ (q\) ">T | \ (\ sim q\) ">F | \ (q\ lor\ sim q\) ">T | \ (p\ cuña (q\ lor\ sim q)\) ">T |
| \ (p\) ">T | \ (q\) ">F | \ (\ sim q\) ">T | \ (q\ lor\ sim q\) ">T | \ (p\ cuña (q\ lor\ sim q)\) ">T |
| \ (p\) ">F | \ (q\) ">T | \ (\ sim q\) ">F | \ (q\ lor\ sim q\) ">T | \ (p\ cuña (q\ lor\ sim q)\) ">F |
| \ (p\) ">F | \ (q\) ">F | \ (\ sim q\) ">T | \ (q\ lor\ sim q\) ">T | \ (p\ cuña (q\ lor\ sim q)\) ">F |
Revisar
Escribe una tabla de verdad para las siguientes variables.
- \((p \wedge q)\lor \sim r\)
- \(p \lor ( \sim q \lor r)\)
- \(p \wedge (q \lor \sim r)\)
- La única diferencia entre #1 y #3 es la colocación del paréntesis. ¿En qué se diferencian las tablas de verdad?
- ¿Cuándo es\(p \lor q \lor r\) verdad?
- \(p \lor q \lor r\)
- \((p \lor q) \lor \sim r\)
- \(( \sim p \wedge \sim q) \wedge r\)
- \(( \sim p \lor \sim q) \wedge r\)
¿Es válido el siguiente argumento? Si es así, ¿qué ley se está utilizando? HINTA: Las declaraciones podrían estar fuera de orden.
\(p \rightarrow q\)
\(r \rightarrow p\)
\(\therefore r \rightarrow q\)
\(p \rightarrow q\)
\(r \rightarrow q\)
\(\therefore p \rightarrow r\)
\(p \rightarrow \sim r\)
\(r \)
\(\therefore \sim p\)
\(\sim q \rightarrow r\)
\(q \)
\(\therefore \sim r\)
\(p \rightarrow (r \rightarrow s)\)
\(p \)
\(\therefore r \rightarrow s\)
\(r \rightarrow q\)
\(r \rightarrow s \)
\(\therefore q \rightarrow s\)
Recursos adicionales
Video: Principios de las Tablas de Verdad
Práctica: Tablas de la Verdad