Inicio
Educación Básica
Geometría
4: Triángulos
4.10: Declaraciones de congruencia

4.10: Declaraciones de congruencia

Última actualización
Guardar como PDF

Page ID: 107516

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Los ángulos y lados correspondientes de los triángulos congruentes son congruentes.

Al afirmar que dos triángulos son congruentes, las partes correspondientes deberán escribirse en el mismo orden. Por ejemplo, si lo sabemos\(\Delta ABC\) y\(\Delta LMN\) somos congruentes entonces sabemos que:

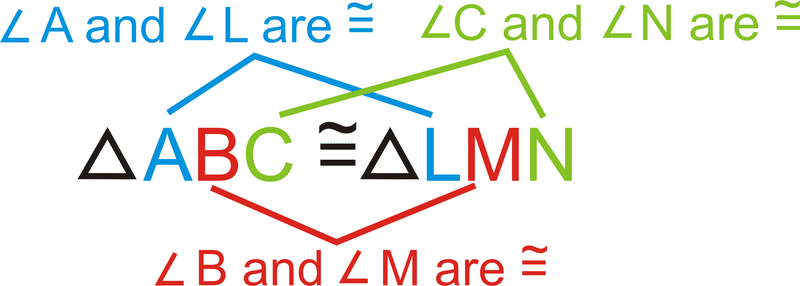
f-d_54cad6455ec7768d0fd6f04f0279cc83c94be645e79de70011f9f11e+image_tiny+image_tiny.png — Figura\(\PageIndex{1}\)

Observe que los lados congruentes también se alinean dentro de la declaración de congruencia.

\(\overline{AB} \cong \overline{LM}\),\(\overline{BC} \cong \overline{MN}\),\(\overline{AC} \cong \overline{LN}\)

También podemos escribir esta declaración de congruencia de otras cinco maneras, siempre y cuando los ángulos congruentes coincidan. Por ejemplo, también podemos escribir\(\Delta ABC\cong \Delta LMN\) como:

\(\begin{align*} \Delta ACB\cong \Delta LNM &\qquad& \Delta BCA\cong \Delta MNL &\qquad& \Delta BAC\cong \Delta MLN \\ \Delta CBA\cong \Delta NML &\qquad& \Delta CAB\cong \Delta NLM \end{align*}\)

¿Y si te dijeran eso\(\Delta FGH\cong \Delta XYZ\)? ¿Cómo podría determinar con qué lado\(\Delta XYZ\) es congruente\(\overline{GH}\) y con qué ángulo es congruente\(\angle F\)?

Ejemplo\(\PageIndex{1}\)

Si\(\Delta ABC\cong \Delta DEF\), ¿qué más sabes?

Solución

De esta declaración de congruencia, sabemos que tres pares de ángulos y tres pares de lados son congruentes.

\(\angle A\cong \angle D,\angle B\cong \angle E\),\ ángulo C\ cong\ ángulo F\),

\(\overline{AB} \cong \overline{DE} , \overline{BC} \cong \overline{EF} , \overline{AC} \cong \overline{DF}\).

Ejemplo\(\PageIndex{2}\)

Si\( \Delta KBP\cong \Delta MRS\), ¿qué más sabes?

Solución

De esta declaración de congruencia, sabemos que tres pares de ángulos y tres pares de lados son congruentes.

\(\angle K\cong \angle M,\:\angle B\cong \angle R,\:\angle P\cong \angle S\),

\(\overline{KB} \cong \overline{MR} ,\:\overline{BP} \cong \overline{RS}, \: \overline{KP} \cong \overline{MS}\).

Ejemplo\(\PageIndex{3}\)

Escribe una declaración de congruencia para los dos triángulos a continuación.

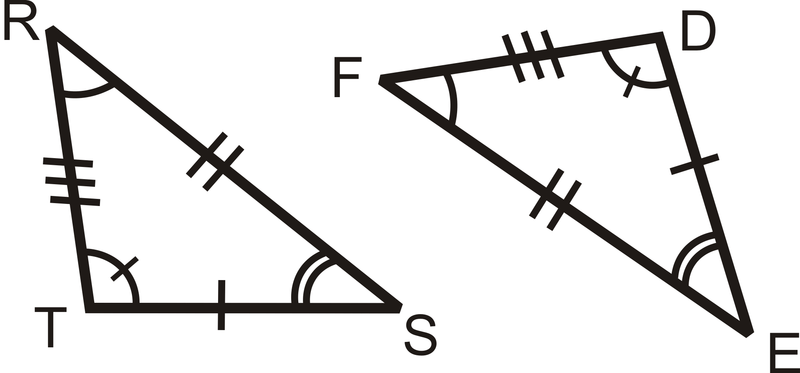
f-d_a7a2bec1d9b3a9314505edf69bfcf149f66f6a624069d39379aed245+image_tiny+image_tiny.png — Figura\(\PageIndex{2}\)

Solución

Alinee los ángulos correspondientes en los triángulos:

\(\angle R\cong \angle F,\:\angle S\cong \angle E\:and \angle T\cong \angle D\).

Por lo tanto, una posible declaración de congruencia es\(\Delta RST\cong \angle FED\)

Ejemplo\(\PageIndex{4}\)

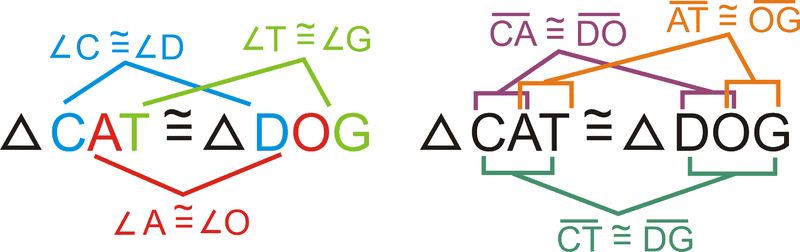
Si\(\Delta CAT\cong \Delta DOG\), ¿qué más sabes?

Solución

De esta declaración de congruencia, sabemos que tres pares de ángulos y tres pares de lados son congruentes.

f-d_db15c6e53da10803ffedb0eb93f0160053e2e2c02b10576839bd8921+image_tiny+image_tiny+image_tiny.png — Figura\(\PageIndex{3}\)

Ejemplo\(\PageIndex{5}\)

Si\(\Delta BUG\cong \Delta ANT\), ¿a qué ángulo es congruente\(\angle N\)?

Solución

Ya que el orden de las letras en la declaración de congruencia nos dice qué ángulos son congruentes,\(\angle N\cong \angle U\) porque cada uno es el segundo de las tres letras.

Revisar

Para las preguntas 1-4, determinar si los triángulos son congruentes utilizando la definición de triángulos congruentes. Si lo son, escriba la declaración de congruencia.

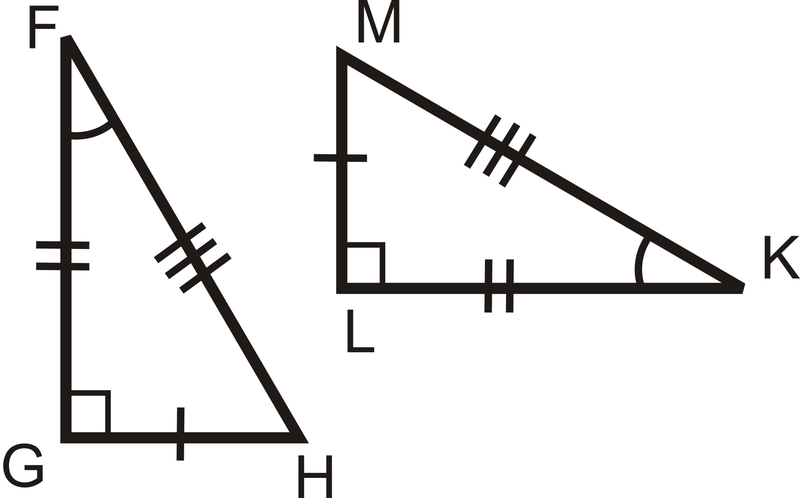
Figura\(\PageIndex{4}\)
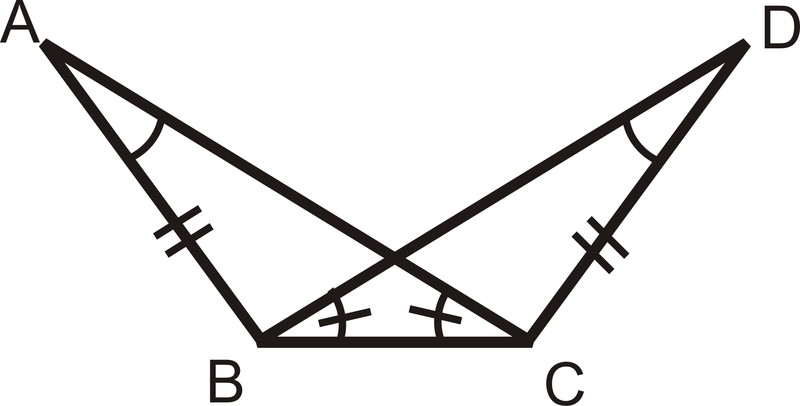
Figura\(\PageIndex{5}\)
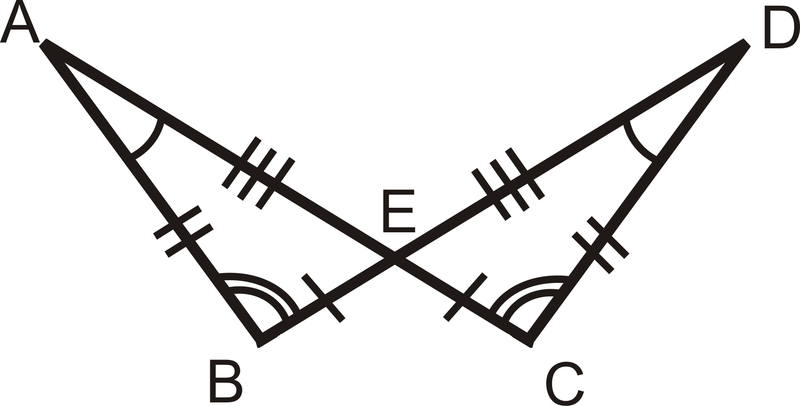
Figura\(\PageIndex{6}\)
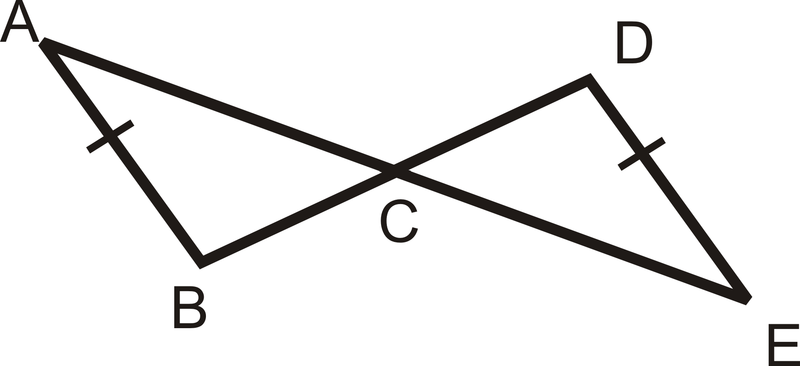
Figura\(\PageIndex{7}\)
Supongamos que los dos triángulos de abajo son congruentes. Escribe una declaración de congruencia para estos triángulos.

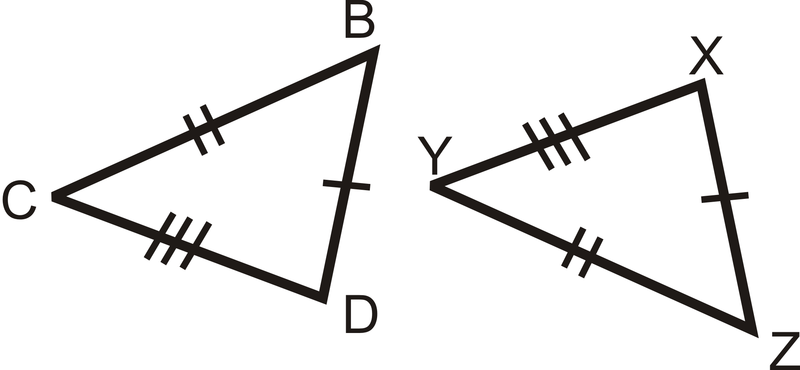
Figura\(\PageIndex{8}\)
Explique cómo sabemos que si los dos triángulos son congruentes, entonces\(\angle B\cong \angle Z\).
Si\(\Delta TBS\cong \Delta FAM\), ¿qué más sabes?
Si\(\Delta PAM\cong \Delta STE\), ¿qué más sabes?
Si\(\Delta INT\cong \Delta WEB\), ¿qué más sabes?
Si\(\Delta ADG\cong \Delta BCE\), ¿a qué ángulo es congruente\(\angle G\)?