4.9: CPCTC
- Page ID
- 107502
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los lados y ángulos de los triángulos congruentes tienen la misma medida.
Triángulos congruentes
Dos figuras son congruentes si tienen exactamente el mismo tamaño y forma. Si dos triángulos son congruentes, tendrán exactamente los mismos tres lados y exactamente los mismos tres ángulos. En otras palabras, dos triángulos son congruentes si puedes girar, voltear y/o deslizar uno para que encaje exactamente en el otro.
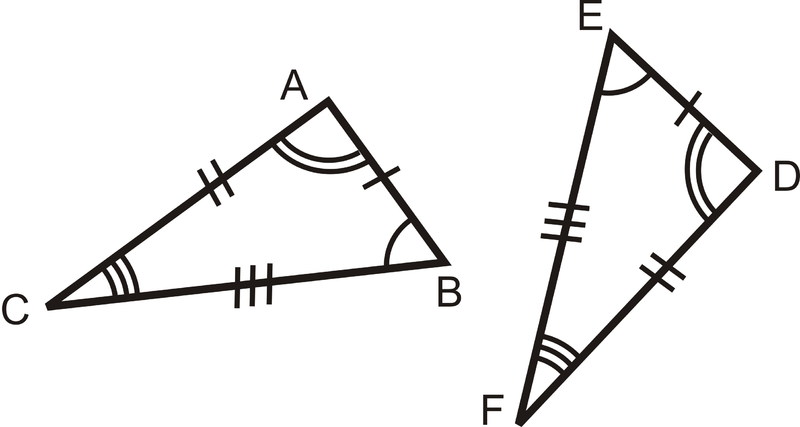
\(\Delta ABC\)y\(\Delta DEF\) son congruentes porque
\(\begin{align*}\overline{AB}\cong DE &\qquad& \angle A\cong \angle D \\ \overline{BC}\cong EF\overline{AB}&\:and\:& \angle B\cong \angle E \\ \overline{AC}\cong \overline{DF} &\qquad& \angle C\cong \angle F \end{align*}\)
Observe que cuando dos triángulos son congruentes sus tres pares de ángulos correspondientes y sus tres pares de lados correspondientes son congruentes.
Al hacer referencia a partes congruentes correspondientes de triángulos congruentes, puede usar la frase C orespondiendo P artes de C ongruentes T riángulos son C ongruentes, o su abreviatura CPCTC.
¿Y si te dieran dos triángulos con todas las medidas de ángulo y todas las longitudes laterales marcadas? ¿Cómo podrías saber si los dos triángulos eran congruentes?
Ejemplo\(\PageIndex{1}\)
Determinar si los triángulos son congruentes usando la definición de triángulos congruentes.
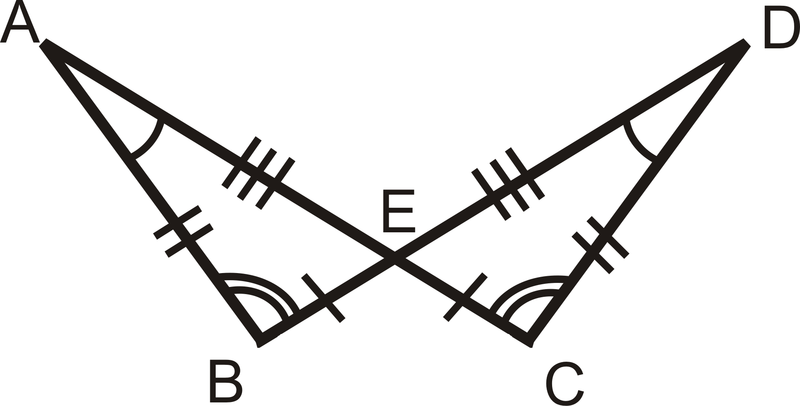
Solución
Podemos ver por las marcas que\(\angle B\cong \angle C\),\(\angle A\cong \angle D\), y\(\angle AEB\cong \angle DEC\) porque son ángulos verticales. También, sabemos que\(\overline{BA}\cong \overline{CD}\),\(\overline{EA}\cong \overline{ED}\), y\(\overline{BE}\cong \overline{CE}\). Debido a que tres pares de lados y tres pares de ángulos son todos congruentes y son partes correspondientes, esto significa que los dos triángulos son congruentes.
Ejemplo\(\PageIndex{2}\)
Determinar si los triángulos son congruentes usando la definición de triángulos congruentes.
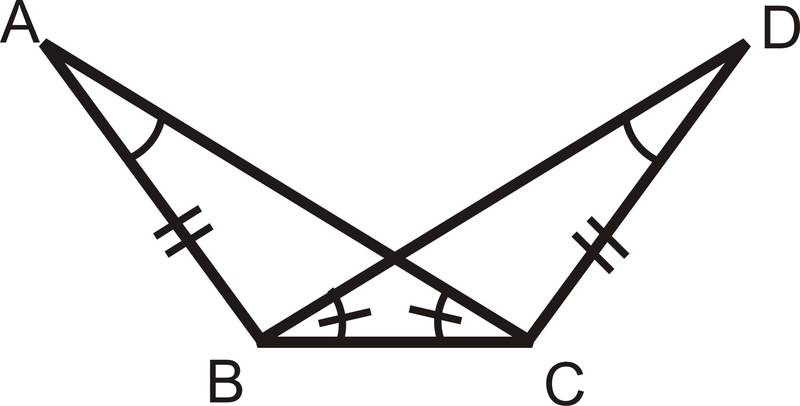
Solución
Si bien hay partes correspondientes congruentes, sólo hay dos pares de lados congruentes, los marcados y el lado compartido. Sin saber si el tercer par de lados es congruente o no no podemos decir si los triángulos son congruentes usando la definición de triángulos congruentes. Tenga en cuenta, esto no quiere decir que los triángulos no sean congruentes, solo significa que necesitamos más información para decir que son congruentes usando la definición de triángulos congruentes (los triángulos congruentes tienen tres pares de ángulos congruentes y tres pares de lados congruentes).
Ejemplo\(\PageIndex{3}\)
¿Los dos triángulos de abajo son congruentes?
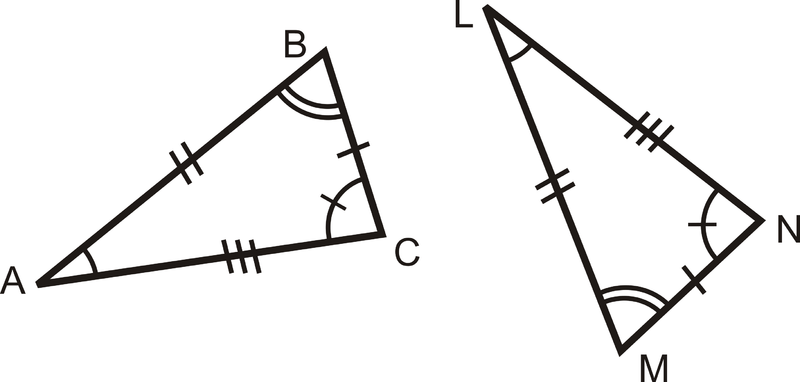
Solución
Para determinar si los triángulos son congruentes, empareja los lados superiores con el mismo número de marcas de tic:\(\overline{BC}\cong \overline{MN}\),\(\overline{AB}\cong \overline{LM}\),\(\overline{AC}\cong \overline{LN}\).
A continuación, haga coincidir los ángulos con las mismas marcas:
\(\angle A\cong \angle L\),\(\angle B\cong \angle M\), y\(\angle C\cong \angle N\).
Por último, debemos asegurarnos de que estas son partes correspondientes. Para ello, comprueba si los ángulos congruentes son lados congruentes opuestos. Aquí,\(\angle A\) es opuesto\(\overline{BC}\) y\(\angle L\) es opuesto\(\overline{MN}\). Porque\(\angle A\cong \angle L\) y\(\overline{BC}\cong \overline{MN}\), son correspondientes. Haciendo esta comprobación para los otros lados y ángulos, vemos que todo coincide y los dos triángulos son congruentes.
Ejemplo\(\PageIndex{4}\)
Si los tres pares de ángulos para dos triángulos dados son congruentes, ¿significa eso que los triángulos son congruentes?
Solución
Sin saber nada de las longitudes de los lados no se puede decir si dos triángulos son congruentes o no. Los dos triángulos descritos anteriormente podrían ser congruentes, pero necesitaríamos más información para saber con certeza.
Ejemplo\(\PageIndex{5}\)
Determinar si los triángulos son congruentes usando la definición de triángulos congruentes.
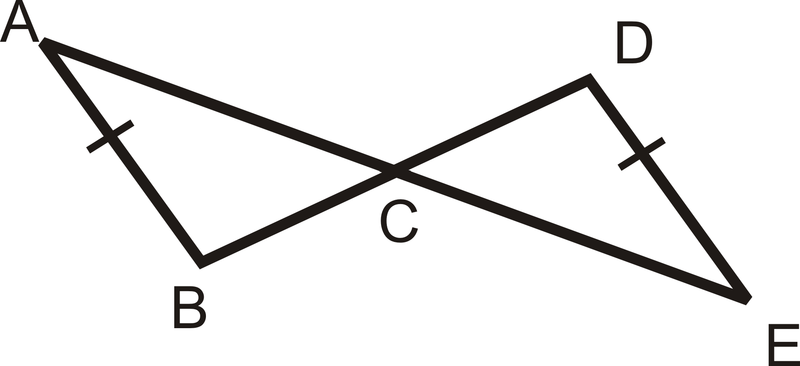
Solución
De las marcas de tic podemos ver eso\(\overline{AB}\cong \overline{DE}\). También lo sabemos\(\angle ACB\cong \angle ECD\) porque son ángulos verticales. Sin embargo, esta no es suficiente información para saber si los triángulos son congruentes o no.
Revisar
Las siguientes ilustraciones muestran dos líneas paralelas cortadas por una transversal (Se puede suponer que aunque las líneas no estén marcadas paralelas, las dos líneas que parecen paralelas, en realidad lo son). ¿Los triángulos formados por ellos son definitivamente congruentes?
-
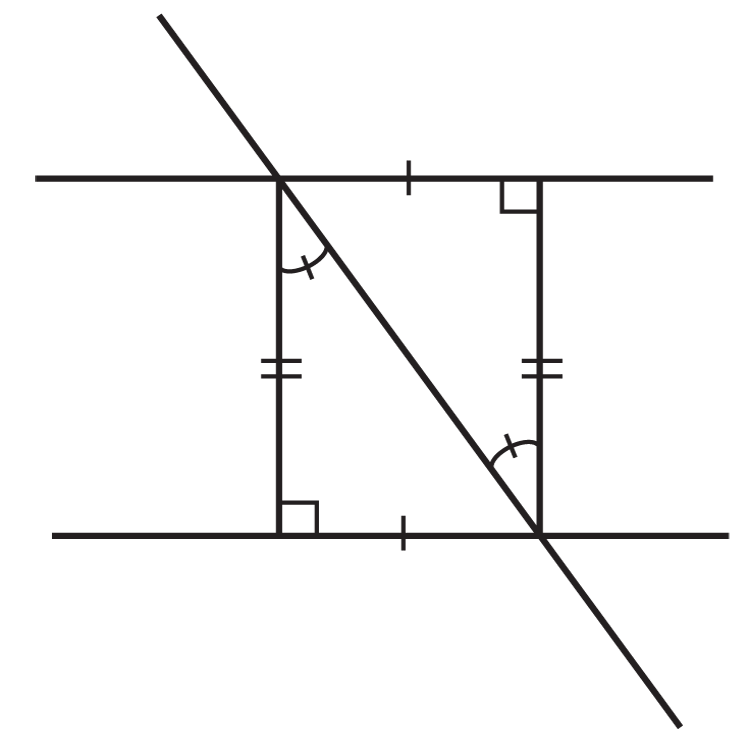
Figura\(\PageIndex{6}\) -
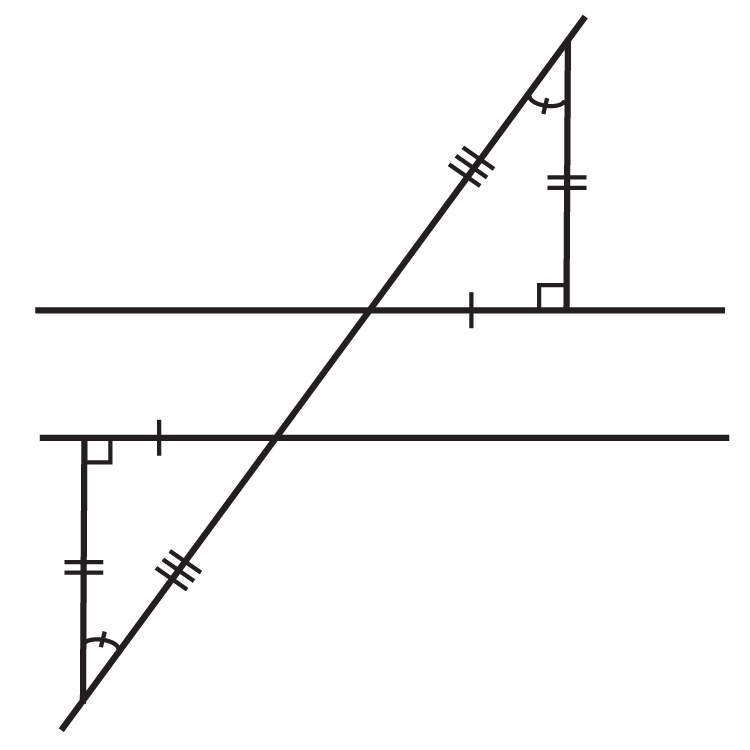
Figura\(\PageIndex{7}\) -
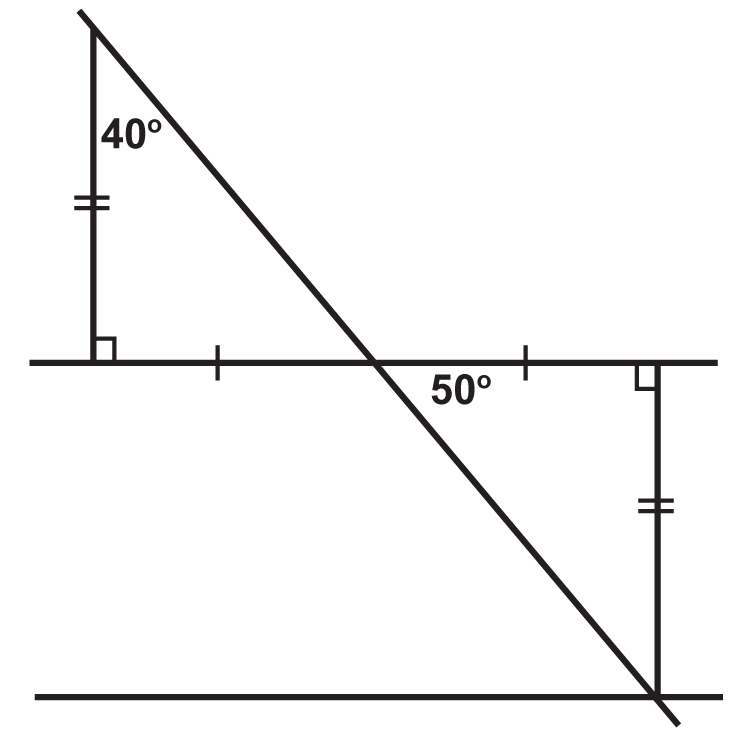
Figura\(\PageIndex{8}\) -
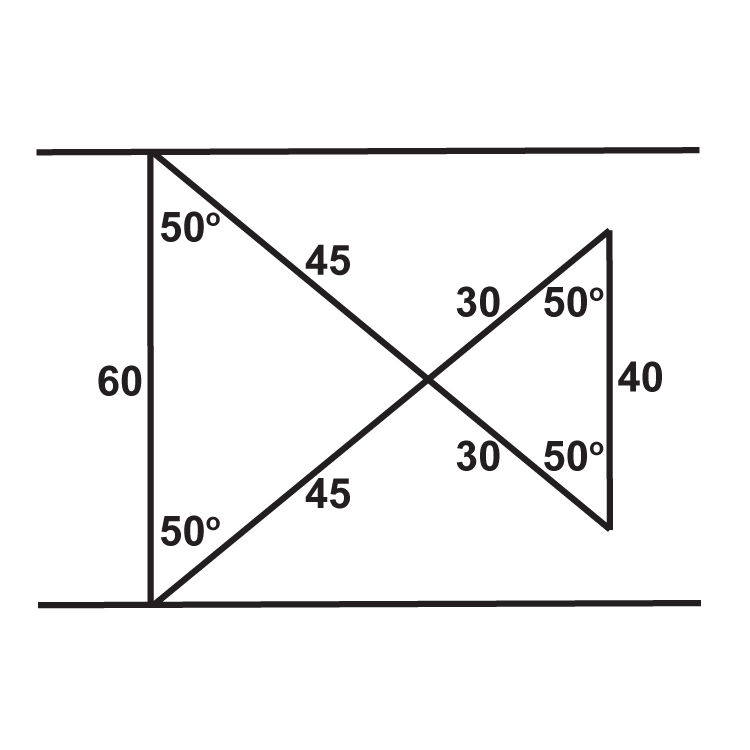
Figura\(\PageIndex{9}\) -
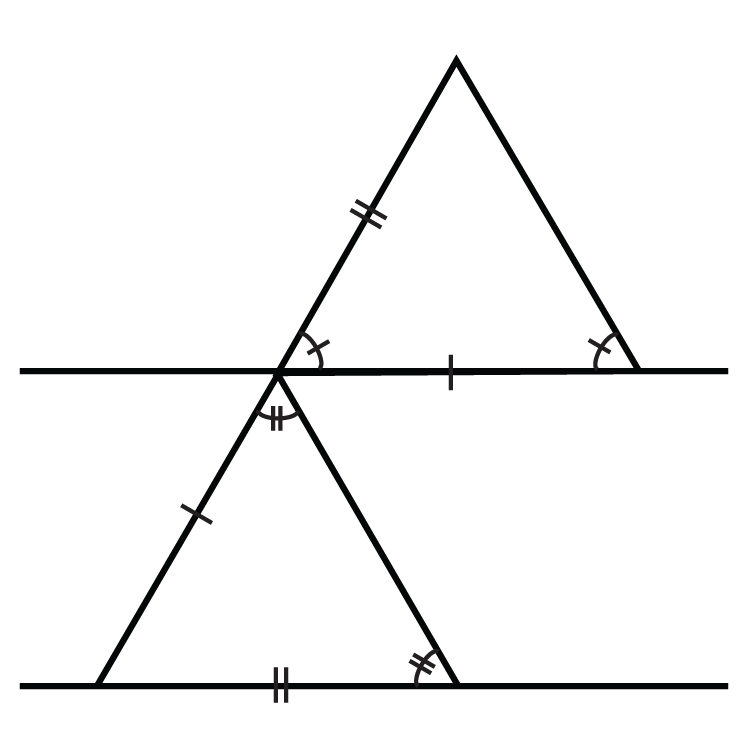
Figura\(\PageIndex{10}\)
Con base en los siguientes detalles, ¿los triángulos son definitivamente congruentes?
- Ambos triángulos son triángulos rectos en los que mide un ángulo\(55^{\circ}\). Todos sus lados correspondientes son congruentes.
- Ambos triángulos son triángulos equiangulares.
- Ambos triángulos son triángulos equiláteros. Todos los lados son de 5 pulgadas de largo.
- Ambos triángulos son triángulos obtusos en los que mide un ángulo\(35^{\circ}\). Dos de sus lados correspondientes son congruentes.
- Ambos triángulos son triángulos obtusos en los que dos de sus ángulos miden\(40^{\circ}\) y\(20^{\circ}\). Todos sus lados correspondientes son congruentes.
- Ambos triángulos son triángulos isósceles en los que mide un ángulo\(15^{\circ}\).
- Ambos triángulos son triángulos isósceles con dos ángulos iguales de\(55^{\circ}\). Todos los lados correspondientes son congruentes.
- Ambos triángulos son triángulos agudos en los que dos de sus ángulos miden\(40^{\circ}\) y\(80^{\circ}\). Todos sus lados correspondientes son congruentes.
- Ambos triángulos son triángulos agudos en los que mide un ángulo\(60^{\circ}\). Dos de sus lados correspondientes son congruentes.
- Ambos triángulos son triángulos equiláteros.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.3.
Recursos
vocabulario
| Término | Definición |
|---|---|
| Teorema del Tercer Ángulo | Si dos ángulos en un triángulo son congruentes con dos ángulos en otro triángulo, entonces el tercer par de ángulos también es congruente. |
Recursos adicionales
Elemento Interactivo
Video: Triángulos Congruentes y Similares
Actividades: Triángulos Congruentes Preguntas de Discusión
Ayudas de estudio: Guía de estudio de congruencia triangular
Práctica: CPCTC
Mundo Real: Triángulos Congruentes

