4.12: Triángulos congruentes
- Page ID
- 107568
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Verificar congruencia con SSS, SAS, RHS y ASA
Aplicaciones de Triángulos Congruentes
Dos triángulos son congruentes si y sólo si los pares correspondientes de lados y los pares correspondientes son congruentes.
La siguiente lista resume los diferentes criterios que se pueden utilizar para mostrar congruencia triangular:
- AAS (Angle-Angle-Side): Si dos triángulos tienen dos pares de ángulos congruentes, y un lado no común de los ángulos en un triángulo es congruente con el lado correspondiente en el otro triángulo, entonces los triángulos son congruentes.
- ASA (Angle-Side-Angle): Si dos triángulos tienen dos pares de ángulos congruentes y el lado común de los ángulos (el lado entre los ángulos congruentes) en un triángulo es congruente con el lado correspondiente en el otro triángulo, entonces los triángulos son congruentes.
- SAS (Side-Angle-Side): Si dos triángulos tienen dos pares de lados congruentes y el ángulo incluido en un triángulo es congruente con el ángulo incluido en el otro triángulo, entonces los triángulos son congruentes.
- SSS (Lado Lateral): Si dos triángulos tienen tres pares de lados congruentes, entonces los triángulos son congruentes.
- Solo triángulos rectos: HL (Hipotenusa-Pierna): Si dos triángulos rectos tienen un par de piernas congruentes e hipotenusas congruentes, entonces los triángulos son congruentes.
Si dos triángulos no satisfacen al menos uno de los criterios anteriores, no puede estar seguro de que son congruentes.
Elemento interactivo
Reconocer bisectores perpendiculares
En el triángulo de abajo,\ overline {BC} es la bisectriz perpendicular de AD\ overline {AB}. Por lo tanto\ overline {AC}\ cong\ overline {CD}. Además, m\ ángulo ACB=90^ {\ circ} y m\ ángulo DCB=90^ {\ circ}, así que\ ángulo ACB\ cong\ ángulo DCB. También sabes que\ overline {BC} es un lado de ambos triángulos, y es claramente congruente consigo mismo (esto se llama la propiedad reflexiva).

Los triángulos son congruentes por SAS. Tenga en cuenta que aunque estos sean triángulos rectos, no usaría HL para mostrar congruencia triangular en este caso ya que no se le da que las hipotenusas son congruentes.
Ángulos de medición
Utilizando la información del problema anterior, si\(m\angle A=50^{\circ}\), ¿qué es\(m\angle D\)?
\(m\angle D=50^{\circ}\)
Dado que los triángulos son congruentes, todos sus ángulos y lados correspondientes deben ser congruentes. \ ángulo A\) y\ ángulo D\) son ángulos correspondientes, entonces\(\angle A\cong \angle D\).
Triángulos congruentes
¿Una diagonal de un rectángulo divide el rectángulo en triángulos congruentes?
- Recordemos que un rectángulo es un cuadrilátero con cuatro ángulos rectos.
- Los lados opuestos de un rectángulo son congruentes.

Hay información más que suficiente para demostrar que\ (\ Delta EFG\ cong\ Delta GHE)\.
- Método #1: Los triángulos tienen tres pares de lados congruentes, por lo que son congruentes por SSS.
- Método #2: Los triángulos tienen dos pares de lados congruentes y ángulos congruentes incluidos, por lo que son congruentes por SAS.
- Método #3: Los triángulos son triángulos rectos con hipotenusas congruentes y un par de patas congruentes, por lo que son congruentes por HL.
Ejemplo\(\PageIndex{1}\)
Max construye un triángulo usando una herramienta en línea. Le dice a Alicia que su triángulo tiene un ángulo de 42^ {\ circ}, un lado de longitud 12 y un lado de longitud 8. Con sólo esta información, ¿Alicia podrá construir un triángulo que debe ser congruente con el triángulo de Max?
Solución
Si Max también le dijera a Alicia que el ángulo estaba entre los dos lados, entonces podría construir un triángulo que debe ser congruente debido a SAS. Si el ángulo no está entre los dos lados, no puede estar segura de que su triángulo sea congruente porque la SSA no es un criterio para la congruencia triangular. Debido a que Max no declaró dónde estaba el ángulo en relación con los lados, Alicia no puede crear un triángulo que deba ser congruente con el triángulo de Max.
Ejemplo\(\PageIndex{2}\)
¿Los siguientes triángulos son congruentes? Explique.

Solución
Observe que además del par de lados congruentes y el par de ángulos congruentes,\(\overline{AC}\cong \overline{CA}\).
\(\Delta ACB\cong \Delta CAD\)por SAS.
Ejemplo\(\PageIndex{3}\)
¿Los siguientes triángulos son congruentes? Explique.
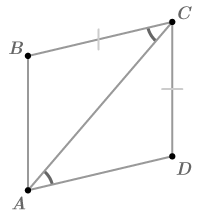
Solución
Los lados congruentes no se corresponden de la misma manera que los ángulos congruentes son correspondientes. La información dada para\(\Delta ACB\) es SAS mientras que la información dada para\(\Delta CAD\) es SSA. Los triángulos no son necesariamente congruentes.
Ejemplo\(\PageIndex{4}\)
\(G\)es el punto medio de\(\overline{EH}\). ¿Los siguientes triángulos son congruentes? Explique.

Solución
Porque G\) es el punto medio de\(\overline{EH}\),\(\overline{EG}\cong \overline{GH}\). También lo sabes\(\angle EGF\cong \angle HGI\) porque son ángulos verticales. \(\Delta EGF\cong \Delta HGI\)por ASA.
Revisar
1. Enumere los cinco criterios para la congruencia del triángulo y dibuje un cuadro que demuestre cada uno.
2. Dados dos triángulos, ¿siempre necesitas al menos tres piezas de información sobre cada triángulo para poder afirmar que los triángulos son congruentes?
Por cada par de triángulos, diga si la información dada es suficiente para mostrar que los triángulos son congruentes. Si los triángulos son congruentes, indique el criterio que utilizó para determinar la congruencia y escriba una declaración de congruencia.
Tenga en cuenta que las imágenes no están necesariamente dibujadas a escala.
3.
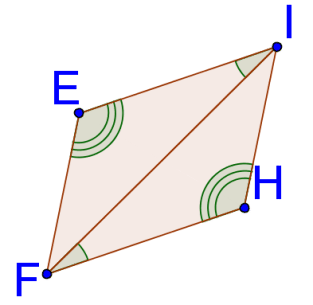
4.
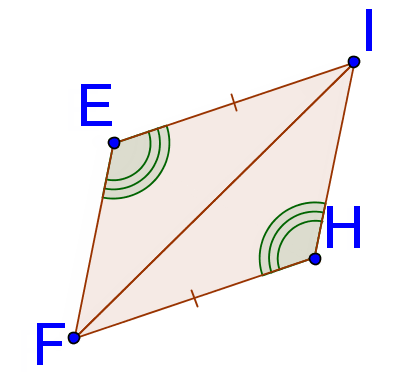
5.
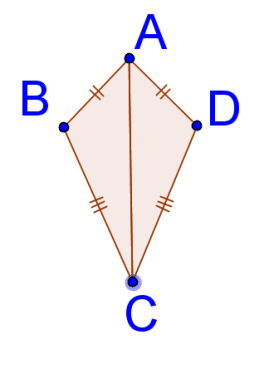
6.
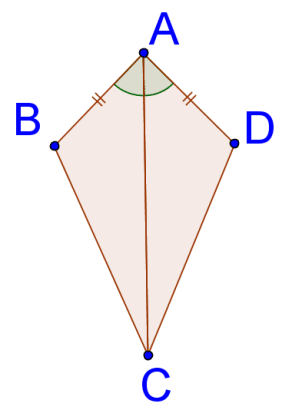
7.
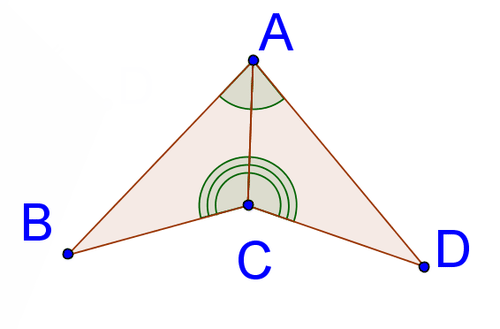
8.
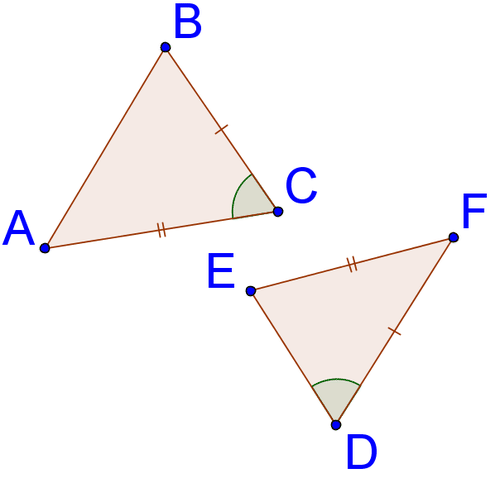
Para el 9-11, indica si la información dada sobre un triángulo oculto sería suficiente para que construyas un triángulo que debe ser congruente con el triángulo oculto. Explique su respuesta.
9. \(\Delta ABC\)con\(m\angle A=72^{\circ},\: AB=6 \:cm, \:BC=8 \:cm.\)
10. \(\Delta ABC\)con\(m\angle A=90^{\circ},\: AB=4 \:cm, \:BC=5 \:cm.\)
11. \(\Delta ABC\)con\(m\angle A=72^{\circ},\: AB=6 \:cm, \:AC=8 \:cm.\)
12. Recordemos que un cuadrado es un cuadrilátero con cuatro ángulos rectos y cuatro lados congruentes. Mostrar y explicar por qué una diagonal de un cuadrado divide el cuadrado en dos triángulos congruentes.
13. Mostrar y explicar usando un criterio diferente para la congruencia triangular por qué una diagonal de un cuadrado divide el cuadrado en dos triángulos congruentes.
14. Recordemos que una cometa es un cuadrilátero con dos pares de lados adyacentes y congruentes. ¿Una de las diagonales de una cometa dividirá la cometa en dos triángulos congruentes? Muestra y explica tu respuesta.
15. En la imagen de abajo,\(G\) se encuentra el punto medio de ambos\(\overline{EH}\) y\(\overline{FI}\). Explique por qué\(\overline{FH}\cong \overline{IE}\) y\(\overline{FE}\cong \overline{HI}\).
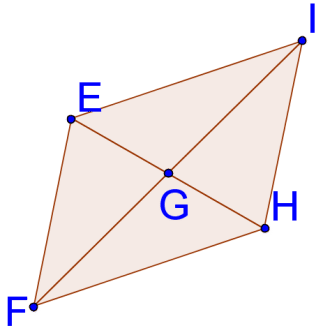
16. Explique por qué AAA no es un criterio para la congruencia triangular.
Reseña (Respuestas)
Para ver las respuestas de la opinión, haga clic aquí.
Recursos adicionales
Video: Triángulos Congruentes y Similares - KA
Práctica: Triángulos congruentes

