4.13: SSS

Tres conjuntos de longitudes laterales iguales determinan la congruencia.

Postulado Lado Lateral

Si 3 lados en un triángulo son congruentes a 3 lados en otro triángulo, entonces los triángulos son congruentes.

Figura\(\PageIndex{1}\)

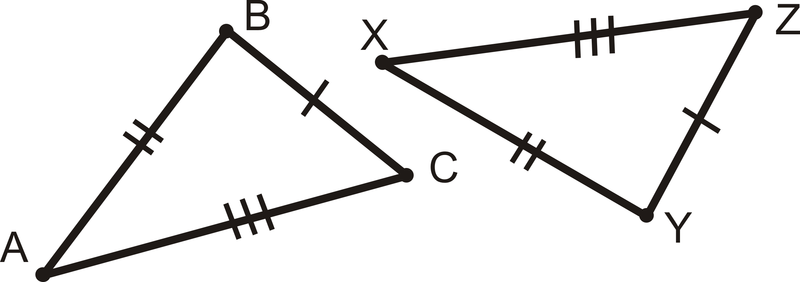
\(\overline{BC}\cong \overline{YZ}\),\(\overline{AB}\cong \overline{XY}\), y\(\overline{AB}\cong \overline{XZ}\) luego\(\Delta ABC \cong \Delta XYZ\).

Esto se llama Postulado Side-Side (SSS) y es un atajo para demostrar que dos triángulos son congruentes. Antes, había que mostrar 3 lados y 3 ángulos en un triángulo eran congruentes a 3 lados y 3 ángulos en otro triángulo. Ahora solo tienes que mostrar 3 lados en un triángulo son congruentes a 3 lados en otro.

¿Y si te dieran dos triángulos y te proporcionaran información solo sobre sus longitudes de lado? ¿Cómo podrías determinar si los dos triángulos eran congruentes?

Ejemplo\(\PageIndex{1}\)

Determinar si los dos triángulos son congruentes.

Figura\(\PageIndex{2}\)

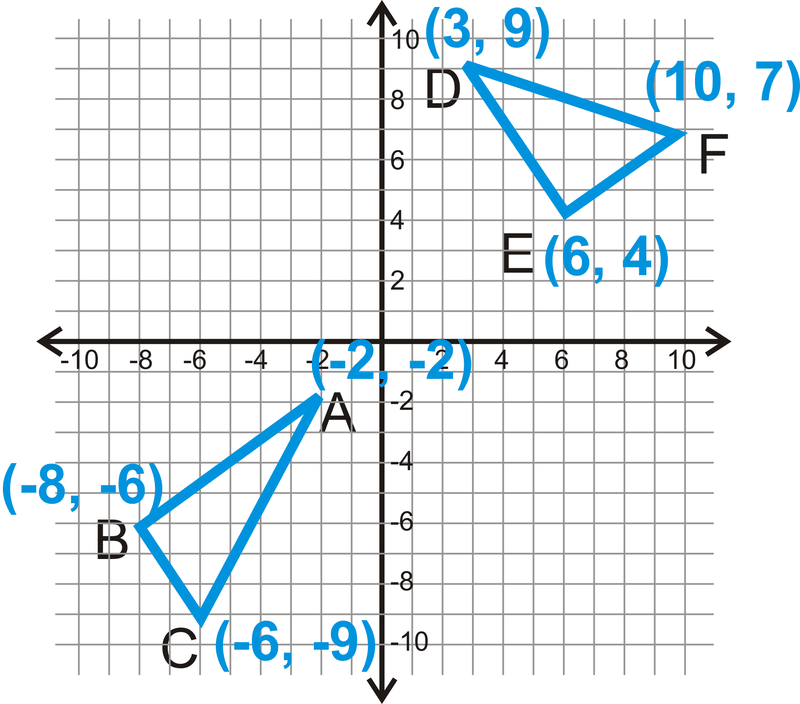
Solución

Empezar con\(\Delta ABC\).

\(\begin{align*} AB &=\sqrt{(−2−(−8))^2+(−2−(−6))^2}\\ &=\sqrt{(6)^2+(4)^2}\\ &=\sqrt{36+16}\\ &=\sqrt{52}\\ &=\sqrt{213} \\ BC&=\sqrt{(−8−(−6))^2+(−6−(−9))^2}\\ &=\sqrt{(−2)^2+(3)^2}\\ &=\sqrt{4+9}\\ &=\sqrt{13} \\ AC&=\sqrt{(−2−(−6))^2+(−2−(−9))^2}\\ &=\sqrt{(4)^2+(7)^2}\\ &=\sqrt{16+49}\\ &=\sqrt{65} \end{align*} \)

Ahora encuentra los lados de\(\Delta DEF\).

\(\begin{align*} DE &=\sqrt{(3−6)^2+(9−4)^2}\\ &=\sqrt{(−3)^2+(5)^2}\\ &=\sqrt{9+25}\\ &=\sqrt{34} \\ EF&=\sqrt{(6−10)^2+(4−7)^2}\\ &=\sqrt{(−4)^2+(−3)^2}\\ &=\sqrt{16+9}\\ &=\sqrt{25}\\ &=5 \\ DF&=\sqrt{(3−10)^2+(9−7)^2}\\ &=\sqrt{(−7)^2+(2)^2}\\ &=\sqrt{49+4}\\ &=\sqrt{53} \end{align*}\)

Ningún lado tiene medidas iguales, por lo que los triángulos no son congruentes.

Ejemplo\(\PageIndex{2}\)

Rellene los espacios en blanco en el comprobante a continuación.

Dado:\( \overline{AB}\cong \overline{DC}\),\(\overline{AC}\cong \overline{DB}\)

Demostrar:\(\Delta ABC\cong \Delta DCB\)

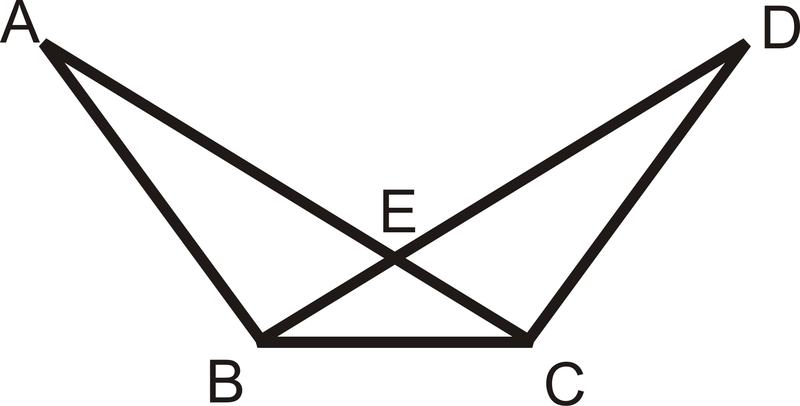Figura\(\PageIndex{4}\)

Solución

Declaración	Razón
1.	1.
2.	2. reflexivo\(PoC\)
3. \(\Delta ABC\cong \Delta DCB\)	3.

Declaración	Razón
1. \(\overline{AB}\cong \overline{DC}, \overline{AC}\cong \overline{DB}\)	1. Dado
2. \(\overline{BC}\cong \overline{CB}\)	2. reflexivo\(PoC\)
3. \(\Delta ABC\cong \Delta DCB\)	3. Postulado SSS

Ejemplo\(\PageIndex{3}\)

Escribe una declaración de congruencia triangular basada en la siguiente imagen:

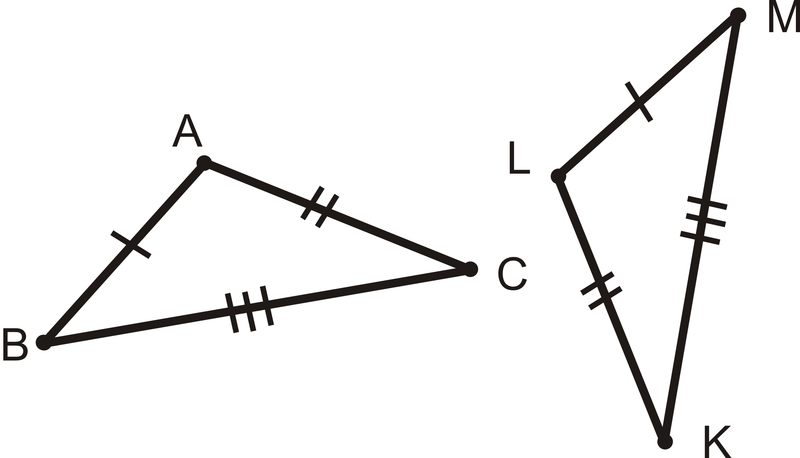Figura\(\PageIndex{5}\)

Solución

De las marcas tic, conocemos AB\ overline {AB}\ cong LM\ overline {AB}\), AC\ overline {AB}\ cong LK\ overline {AB}\),\ overline {BC}\ cong MK\ overline {AB}\). Del Postulado SSS, los triángulos son congruentes. Alineando los lados correspondientes, tenemos\ Delta ABC\ cong\ Delta LMK\).

No olvides PEDIDO IMPORTA al escribir declaraciones de congruencia. Alinee los lados con el mismo número de marcas de tic.

Ejemplo\(\PageIndex{4}\)

Escribe una prueba de dos columnas para demostrar que los dos triángulos son congruentes.

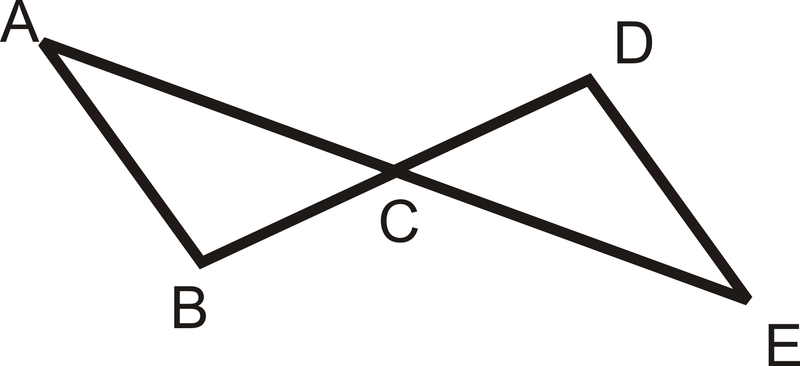Figura\(\PageIndex{6}\)

Dado:\(\overline{AB}\cong \overline{DE}\)

\(C\)es el punto medio de\(\overline{AE}\) y\(\overline{DB}\).

Demostrar:\(\Delta ACB\cong \Delta ECD\)

Solución

Declaración	Razón
1. \(\overline{AB}\cong \overline{DE}\) \(C\)es el punto medio de\(\overline{AE} and \(\overline{DB}\)	1.Dado
2. \(\overline{AC}\cong \overline{CE}, \overline{BC}\cong \overline{CD}\)	2.Definición de un punto medio
3. \(\Delta ACB\cong \Delta ECD\)	3.Postulado SSS

Tenga en cuenta que debe indicar claramente que los tres conjuntos de lados son congruentes ANTES de afirmar que los triángulos son congruentes.

Ejemplo\(\PageIndex{5}\)

La única forma en que mostraremos que dos triángulos son congruentes en un\(x−y\) plano es usando SSS.

Encuentra las longitudes de todos los segmentos de línea de ambos triángulos para ver si los dos triángulos son congruentes.

Solución

Para ello, es necesario utilizar la fórmula de distancia.

Figura\(\PageIndex{7}\)

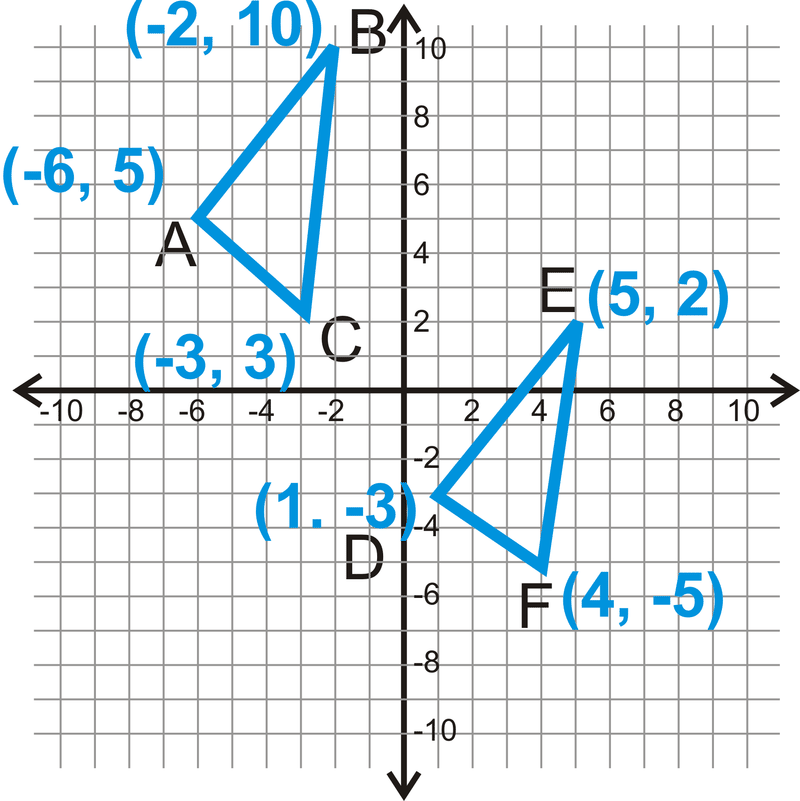
Empezar con\(\Delta ABC\) y sus lados.

\(\begin{align*} AB&=\sqrt{(−6−(−2))^2+(5−10)^2}\\ &=(−4)^2+(−5)^2\\ &=\sqrt{16+25}\\ &=\sqrt{41} \\ BC&=\sqrt{(−2−(−3))^2+(10−3)^2}\\ &=(1)^2+(7)^2\\ &=\sqrt{1+49}\\ &=\sqrt{50}\\ &=\sqrt{52} \\ AC&=\sqrt{(−6−(−3))^2+(5−3)^2}\\ &=\sqrt{(−3)^2+(2)^2}\\ &=\sqrt{9+4}\\ &=\sqrt{13} \end{align*}\)

Ahora, encuentra las longitudes de todos los lados en\(\Delta DEF\).

\(\begin{align*} DE&=\sqrt{(1−5)^2+(−3−2)^2}\\ &=\sqrt{(−4)^2+(−5)^2}\\ &=\sqrt{16+25}\\ &=\sqrt{41} \\ EF&=\sqrt{(5−4)^2+(2−(−5))^2}\\ &=\sqrt{(1)^2+(7)^2}\\ &=\sqrt{1+49}\\ &=\sqrt{50}\\ &=5\sqrt{2}\\ DF&=\sqrt{(1−4)^2+(−3−(−5))^2}\\ &=\sqrt{(−3)^2+(2)^2}\\ &=\sqrt{9+4}\\ &=\sqrt{13} \end{align*}\)

\(AB=DE\),\(BC=EF\), y\(AC=DF\), por lo que los dos triángulos son congruentes por SSS.

Revisar

¿Los pares de triángulos son congruentes? Si es así, escribe la declaración de congruencia y por qué.

1. 

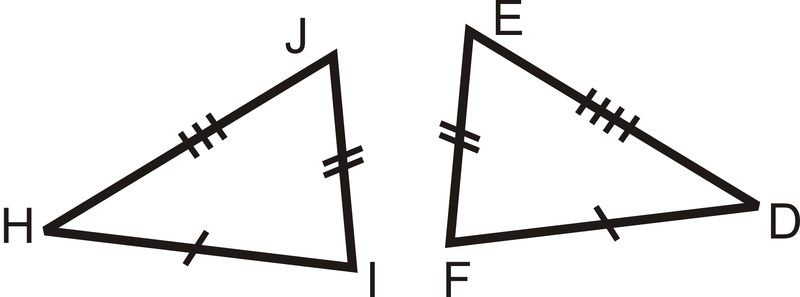
   Figura\(\PageIndex{8}\)

2. 

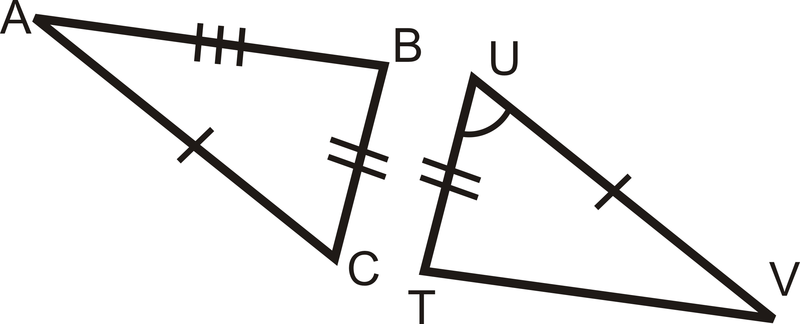
   Figura\(\PageIndex{9}\)

3. 

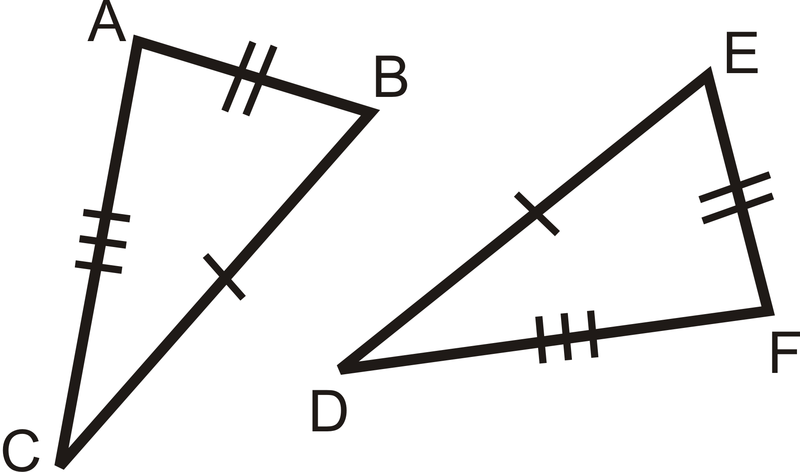
   Figura\(\PageIndex{10}\)

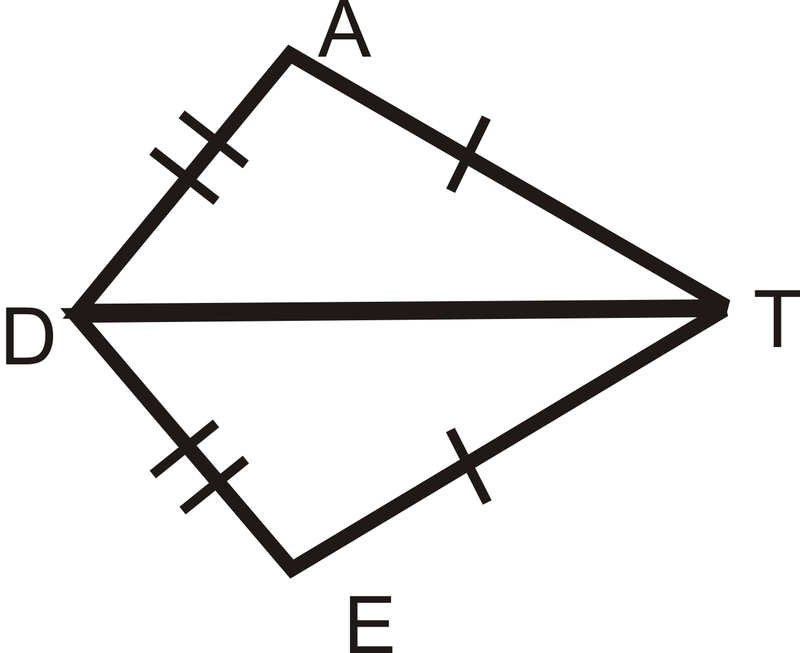4. Figura\(\PageIndex{11}\)

Exponga la información adicional necesaria para mostrar que cada par de triángulos es congruente.

5. Usar SSS

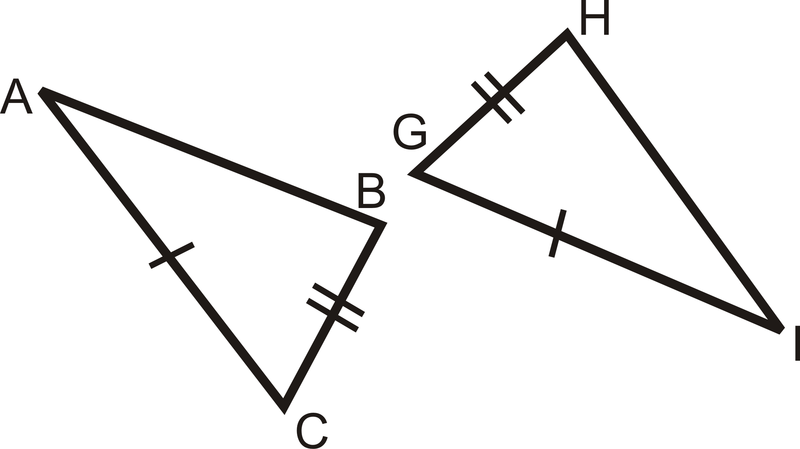   Figura\(\PageIndex{12}\)

6. Usar SSS

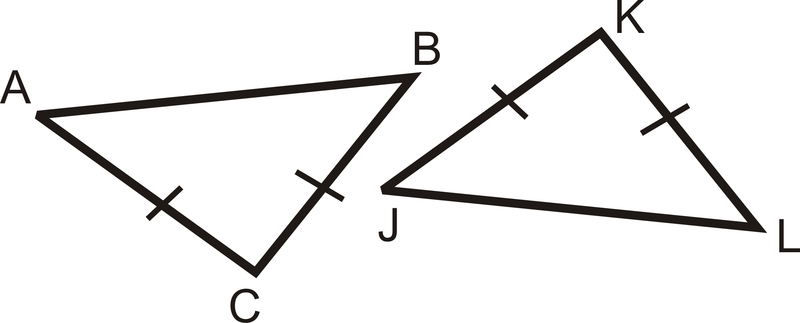   Figura\(\PageIndex{13}\)

Rellene los espacios en blanco en las pruebas a continuación.

7. Dado: B es el punto medio de\(\overline{DC} \overline{AD}\cong \overline{AC}\) Probar:\(\Delta ABD\cong \Delta ABC \)

   

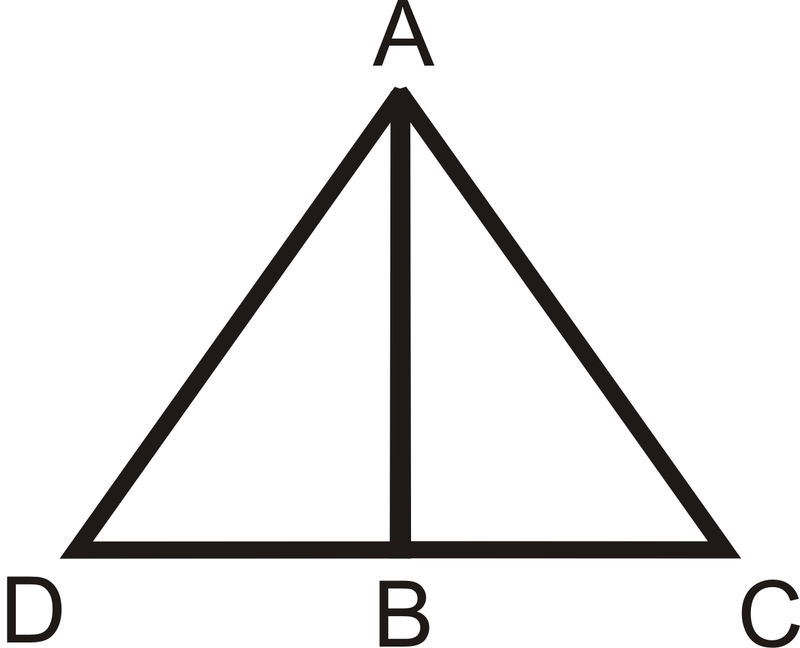
   Figura\(\PageIndex{14}\)

Declaración	Razón
1.	1.
2.	2. Definición de un punto medio
3.	3. reflexivo\(PoC\)
4. \(\Delta ABD\cong \Delta ABC\)	4.

Encuentra las longitudes de los lados de cada triángulo para ver si los dos triángulos son congruentes. Deja tus respuestas bajo el radical.

8. 

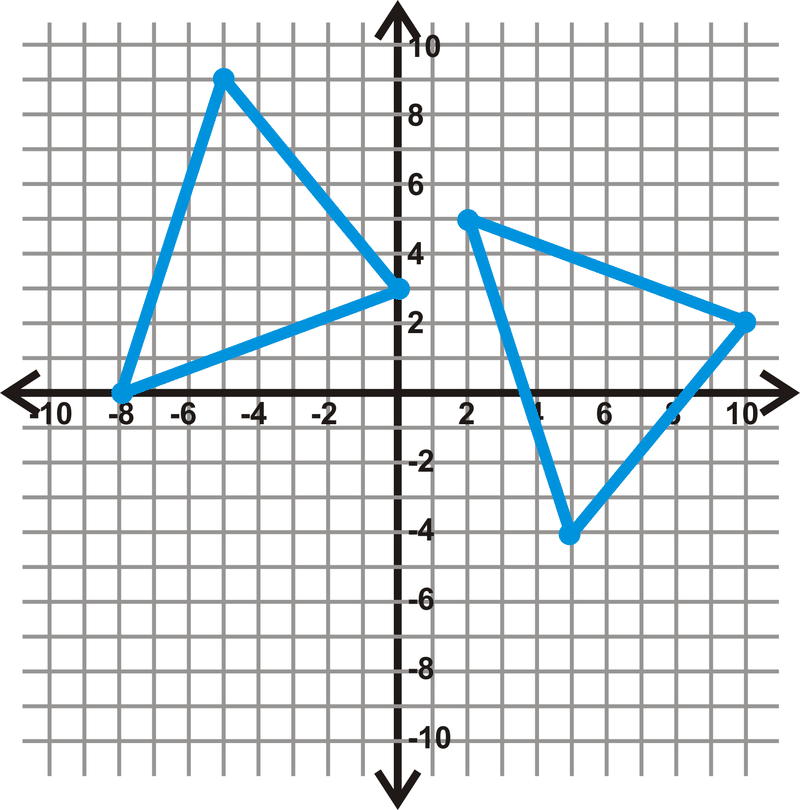
   Figura\(\PageIndex{15}\)

9. 

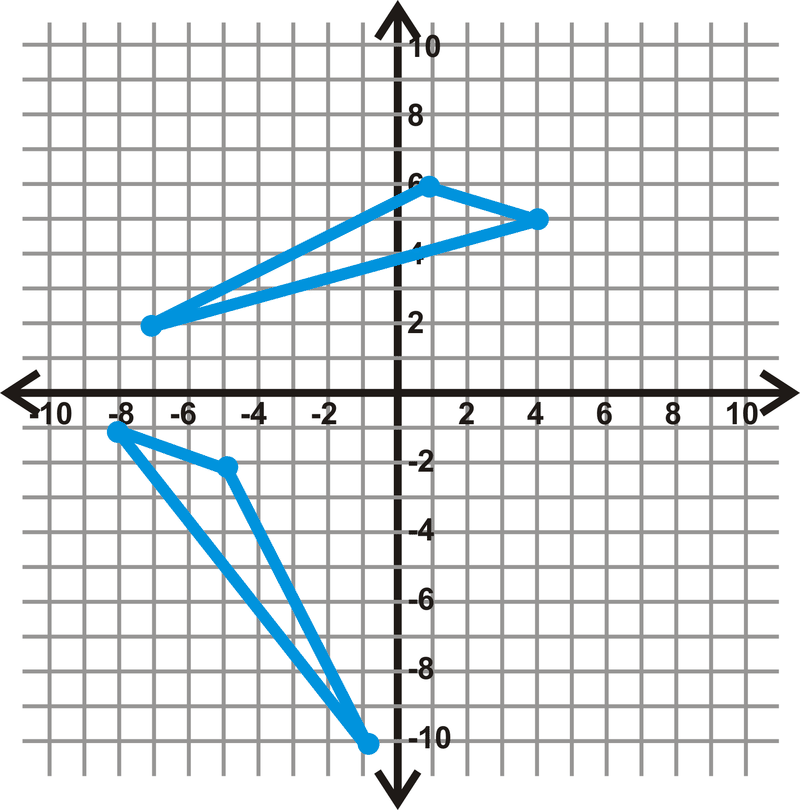
   Figura\(\PageIndex{16}\)

10. \(\Delta ABC: A(−1,5), B(−4,2), C(2,−2)\)y\(\Delta DEF: D(7,−5), E(4,2), F(8,−9)\)
11. \(\Delta ABC: A(−8,−3), B(−2,−4), C(−5,−9)\)y\(\Delta DEF: D(−7,2), E(−1,3), F(−4,8)\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.6.

Recursos

El vocabulario

Término	Definición
Congruente	Las figuras congruentes son idénticas en tamaño, forma y medida.
Fórmula de distancia	La distancia entre dos puntos\((x_1, y_1)\) y se\((x_2, y_2)\) puede definir como\(d=(x_2−x_1)^2+(y_2−y_1)^2\).
Teorema de Congruencia H-L (Hipotenusa-Pierna)	Si la hipotenusa y la pierna en un triángulo rectángulo son congruentes con la hipotenusa y la pierna en otro triángulo rectángulo, entonces los dos triángulos son congruentes.
Triángulo lateral lateral	Un triángulo lateral lateral es un triángulo donde las longitudes de los tres lados son cantidades conocidas.
SSS	SSS significa lado, lado, lado y se refiere al hecho de que los tres lados de un triángulo son conocidos en un problema.
Congruencia del Triángulo	La congruencia del triángulo ocurre si 3 lados en un triángulo son congruentes a 3 lados en otro triángulo.
Transformación Rígida	Una transformación rígida es una transformación que conserva la distancia y los ángulos, no cambia el tamaño ni la forma de la figura.

Recursos adicionales

Elemento Interactivo

Video: Introducción a los triángulos congruentes

Actividades: Congruencia del Triángulo SSS Preguntas de Discusión

Ayudas de estudio: Guía de estudio de congruencia triangular

Práctica: SSS

Mundo Real: Congruencia del Triángulo SSS