4.27: El teorema de Pitágoras
- Page ID
- 107527
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El cuadrado de la hipotenusa equivale a la suma de los cuadrados de las piernas en triángulos rectos.
Los dos lados más cortos de un triángulo rectángulo (los lados que forman el ángulo recto) son las patas y el lado más largo (el lado opuesto al ángulo recto) es la hipotenusa. Para el Teorema de Pitágoras, las piernas son “\(a\)” y “\(b\)” y la hipotenusa es “\(c\)”.
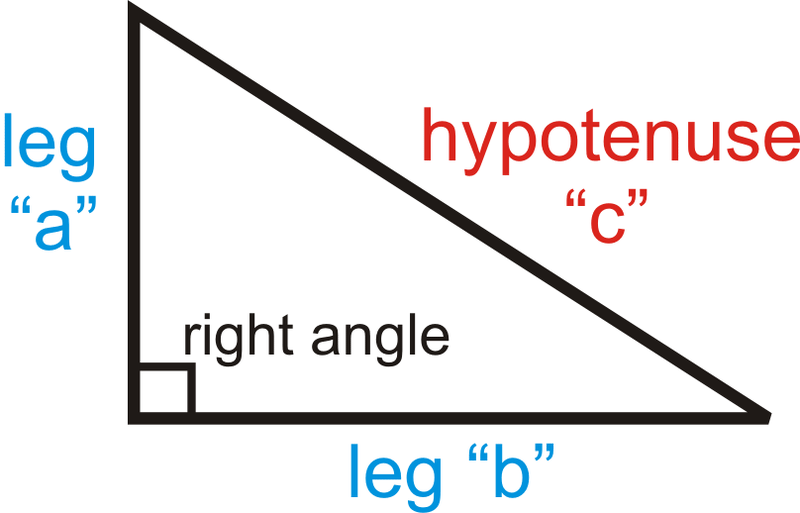
Teorema de Pitágoras: Dado un triángulo rectángulo con patas de longitudes a y b y una hipotenusa de longitud\(c\),\(a^2+b^2=c^2\).
Lo contrario del Teorema de Pitágoras también es cierto. Permite demostrar que un triángulo es un triángulo rectángulo aunque no conozcas sus medidas de ángulo.
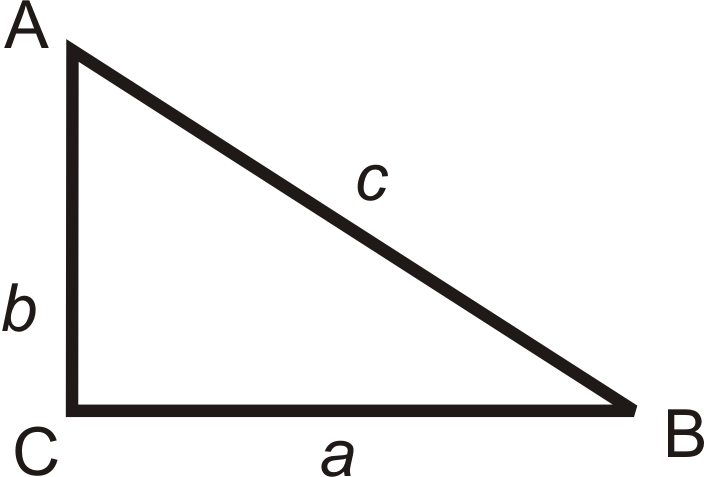
Teorema de Pitágoras Converse: Si el cuadrado del lado más largo de un triángulo es igual a la suma de los cuadrados de los otros dos lados, entonces el triángulo es un triángulo rectángulo.
Si\(a^2+b^2=c^2\), entonces\(\Delta ABC\) es un triángulo rectángulo.
Triples pitagóricos
Una combinación de tres números que hace verdadero el Teorema de Pitágoras se llama triple pitagórico. Cada conjunto de números a continuación es un triple pitagórico.
\(3,4,5 \qquad 5,12,13\qquad 7,24,25\qquad 8,15,17\qquad 9,12,15\qquad 10,24,26\)
Cualquier múltiplo de un triple pitagórico también se considera un triple pitagórico. Multiplicar 3, 4, 5 por 2 da 6, 8, 10, que es otro triple. Para ver si un conjunto de números hace un triple pitagórico, conéctelos al Teorema de Pitágoras.
¿Y si te dijeran que un triángulo tenía longitudes laterales de 5, 12 y 13? ¿Cómo podrías determinar si el triángulo era recto?
Ejemplo\(\PageIndex{1}\)
¿Cuál es la diagonal de un rectángulo con lados 10 y 16?
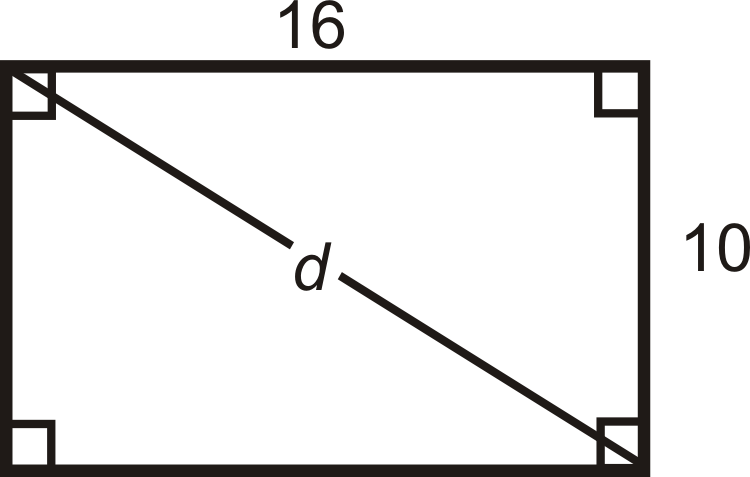
Solución
Para cualquier cuadrado y rectángulo, puedes usar el Teorema de Pitágoras para encontrar la longitud de una diagonal. Enchufe los lados para encontrar\(d\).
\(\begin{align*} 10^2+16^2=d^2 \\ 100+256=d^2 \\ 356&=d^2 \\ d&=\sqrt{356}=2\sqrt{89}\approx 18.87 \end{align*}\)
Ejemplo\(\PageIndex{2}\)
¿Los 6, 7 y 8 hacen los lados de un triángulo rectángulo?
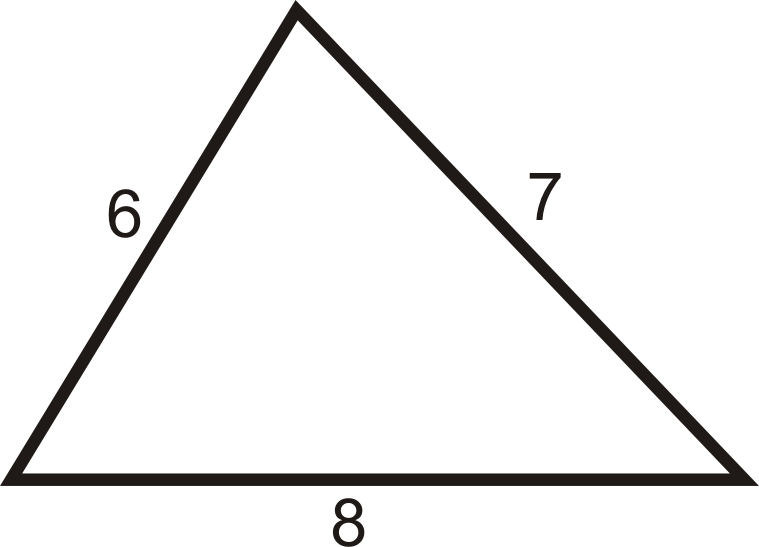
Solución
Enchufa los tres números en el Teorema de Pitágoras. Recuerda que la mayor longitud siempre será la hipotenusa, c. si\(6^2+7^2=8^2\), entonces son los lados de un triángulo rectángulo.
\(\begin{align*} 6^2+7^2&=36+49=85& \\ 8^2&=64&\qquad 85 \neq 64,\: so\: the \:lengths \:are \:not \:the \:sides \:of \:a \:right \:triangle.\end{align*}\)
Ejemplo\(\PageIndex{3}\)
Encuentra la longitud de la hipotenusa.
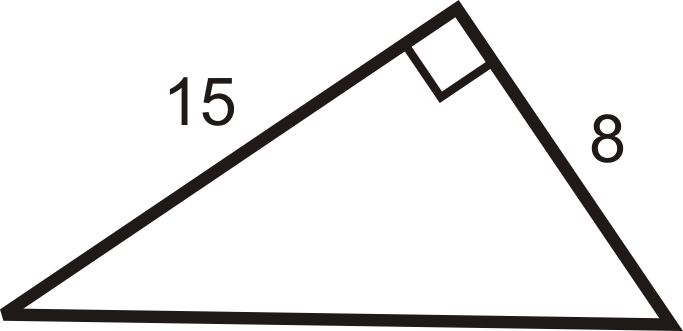
Solución
Usa el Teorema de Pitágoras. Establecer\(a=8\) y\(b=15\). Resolver para\(c\).
\(\begin{align*} 8^2+152&=c^2 \\ 64+225&=c^2 \\ 289&=c^2 \qquad Take\: the \:square \:root \:of \:both \:sides. \\ 172&=c\end{align*}\)
Ejemplo\(\PageIndex{4}\)
¿20, 21, 29 es un triple pitagórico?
Solución
Si\(20^2+21^2=29^2\), entonces el conjunto es un triple pitagórico.
\(\begin{align*} 20^2+21^2&=400+441=841 \\ 29^2&=841 \end{align*}\)
Por lo tanto, 20, 21 y 29 es un triple pitagórico.
Ejemplo\(\PageIndex{5}\)
Determina si los triángulos de abajo son triángulos rectos.
Comprueba si las tres longitudes satisfacen el Teorema de Pitágoras. Que el lado más largo represente c.
Solución
-
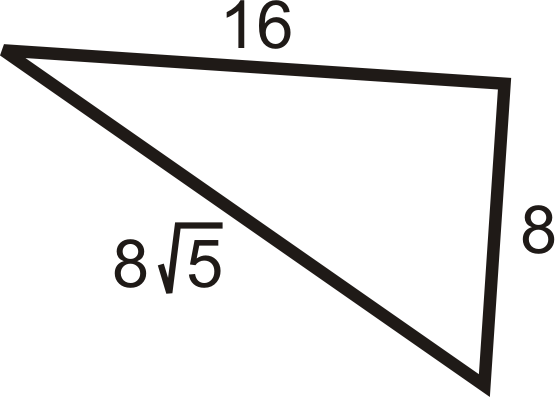
Figura\(\PageIndex{6}\)
\(\begin{align*} a^2+b^2&=c^2 \\ 82+162 &\stackrel{?}{=}(8\sqrt{5})2 \\ 64+256 &\stackrel{?}{=}64\cdot 5 \\ 320&=320\qquad Yes\end{align*} \)
-
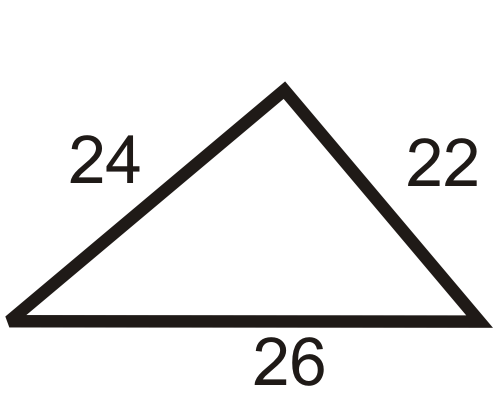
Figura\(\PageIndex{7}\)
\(\begin{align*} a^2+b^2&=c^2 \\ 22^2+24^2&\stackrel{?}{=}262 \\ 484+576 &\stackrel{?}{=}676 \\ 1060 &\neq 676\qquad No\end{align*}\)
Revisar
Encuentra la longitud del lado faltante. Simplifica todos los radicales.
-
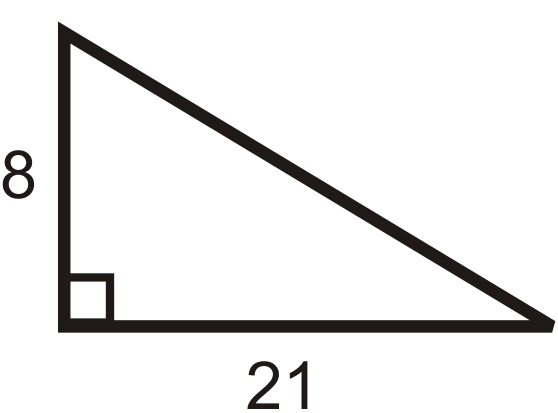
Figura\(\PageIndex{8}\) -
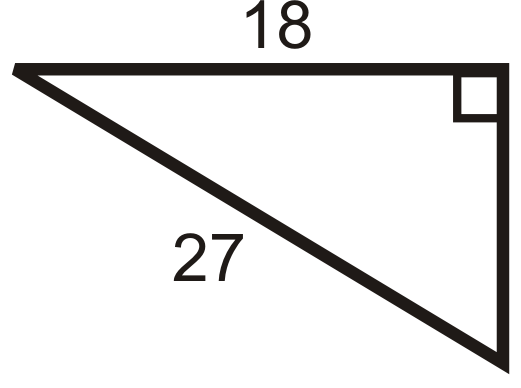
Figura\(\PageIndex{9}\) -
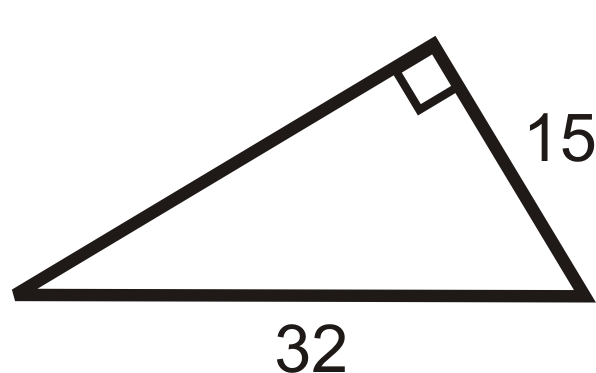
Figura\(\PageIndex{10}\) -
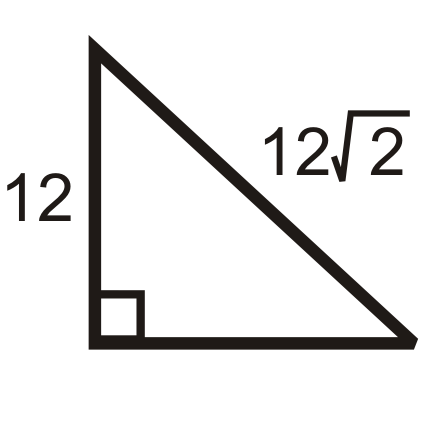
Figura\(\PageIndex{11}\) -
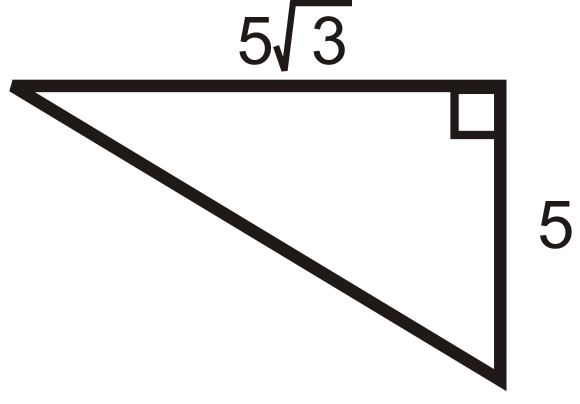
Figura\(\PageIndex{12}\) -
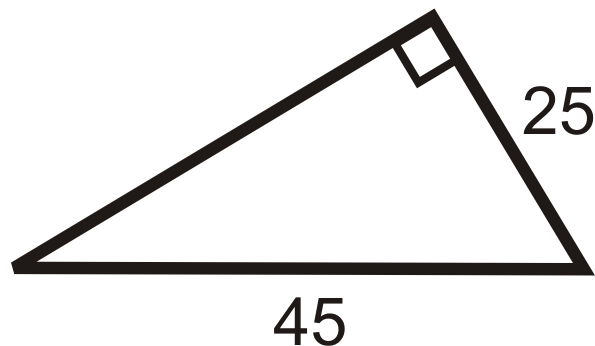
Figura\(\PageIndex{13}\) - Si las patas de un triángulo rectángulo son 10 y 24, entonces la hipotenusa es __________.
- Si los lados de un rectángulo son 12 y 15, entonces la diagonal es _____________.
- Si los lados de un cuadrado son 16, entonces la diagonal es ____________.
- Si los lados de un cuadrado son 9, entonces la diagonal es _____________.
Determina si los siguientes conjuntos de números son Triples Pitágoras.
- 12, 35, 37
- 9, 17, 18
- 10, 15, 21
- 11, 60, 61
- 15, 20, 25
- 18, 73, 75
Determina si las siguientes longitudes forman un triángulo rectángulo.
- 7, 24, 25
- \(\sqrt{5},2\sqrt{10},3\sqrt{5}\)
- \(2\sqrt{3},\sqrt{6},8\)
- 15, 20, 25
- 20, 25, 30
- \(8\sqrt{3},6,2\sqrt{39}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.2.
El vocabulario
| Término | Definición |
|---|---|
| Teorema de Pitágoras | El Teorema de Pitágoras es una relación matemática entre los lados de un triángulo rectángulo\(a^2+b^2=c^2\), dada por, donde a y b son patas del triángulo y c es la hipotenusa del triángulo. |
| Triple pitagórica | Una combinación de tres números que hace cierto el Teorema de Pitágoras. |
| Círculo | Un círculo es el conjunto de todos los puntos a una distancia específica de un punto dado en dos dimensiones. |
| Cónico | Las secciones cónicas son aquellas curvas que se pueden crear por la intersección de un doble cono y un plano. Incluyen círculos, elipses, parábolas e hipérbolas. |
| degenerado cónico | Una cónica degenerada es una cónica que no tiene las propiedades habituales de una sección cónica. Dado que algunos de los coeficientes de la ecuación cónica general son cero, la forma básica de la cónica es meramente un punto, una línea o un par de líneas que se cruzan. |
| Elipse | Las elipses son secciones cónicas que parecen círculos alargados. Una elipse representa todas las ubicaciones en dos cotas que están a la misma distancia de dos puntos especificados llamados focos. |
| hipérbola | Una hipérbola es una sección cónica formada cuando el plano de corte intersecta ambos lados del cono, dando como resultado dos curvas infinitas en forma de “U”. |
| Hipotenusa | La hipotenusa de un triángulo rectángulo es el lado más largo del triángulo rectángulo. Está frente al ángulo recto. |
| Patas de un Triángulo Recto | Las patas de un triángulo rectángulo son los dos lados más cortos del triángulo rectángulo. Las patas están adyacentes al ángulo recto. |
| Parábola | Una parábola es la forma característica de una gráfica de función cuadrática, que se asemeja a una “U”. |
| Número pitagórico triple | Un triple de número pitagórico es un conjunto de tres números enteros a, b y c que satisfacen el Teorema de Pitágoras,\(a^2+b^2=c^2\). |
| Triángulo Recto | Un triángulo rectángulo es un triángulo con un ángulo de 90 grados. |
Recursos adicionales
Elemento Interactivo
Video: Uso de los Principios del Teorema de Pitágoras - Básico
Actividades: Teorema de Pitágoras y Triples Pitágoras Preguntas de Discusión
Ayudas de estudio: Guía de estudio del teorema de Pitágoras
Práctica: El teorema de Pitágoras
Mundo real: Pitágoras TV

