4.38: Distancia entre líneas paralelas
- Page ID
- 107509
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Longitud de un segmento perpendicular entre líneas paralelas.
Todas las líneas verticales están en la forma\(x=a\), donde\(a\) está la\(x\) -intercepción. Para encontrar la distancia entre dos líneas verticales, cuente los cuadrados entre las dos líneas. También puedes usar este método para líneas horizontales. Todas las líneas horizontales están en la forma\(y=b\), donde\(b\) está la\(y\) -intercepción.
En general, la distancia más corta entre dos líneas paralelas es la longitud de un segmento perpendicular entre ellas. Hay infinitamente muchos segmentos perpendiculares entre dos líneas paralelas, pero todos tendrán la misma longitud.
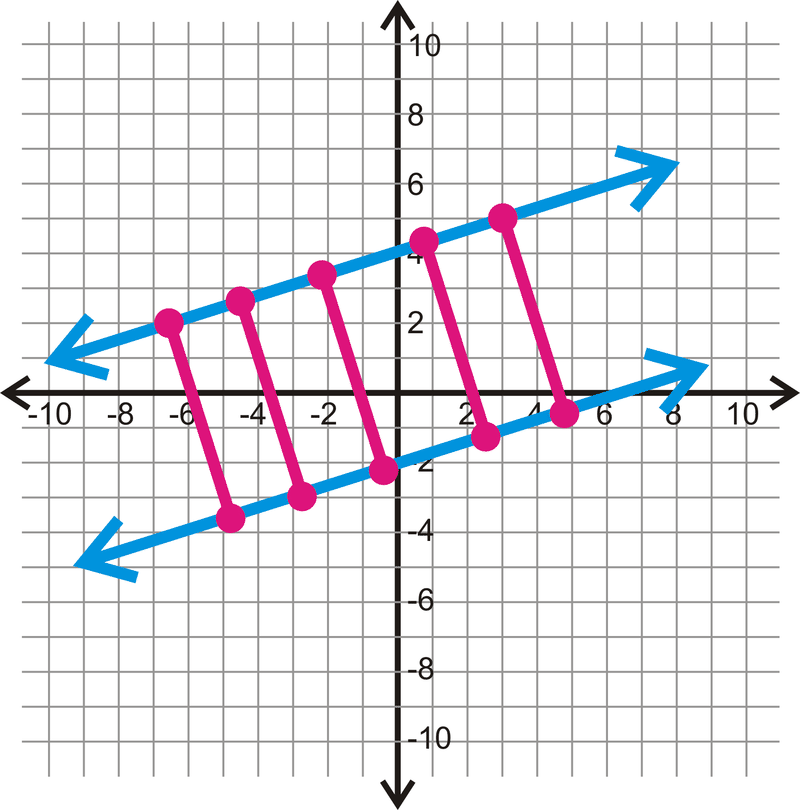
¡Recuerda que las distancias son siempre positivas!
Ejemplo\(\PageIndex{1}\)
Encuentra la distancia entre\(x=3\) y\(x=-5\).
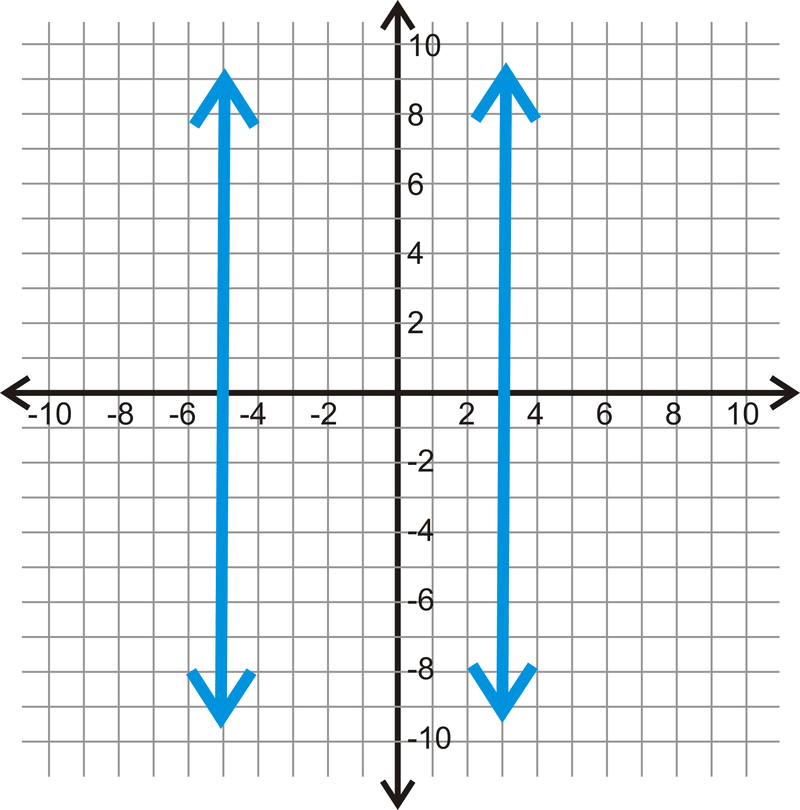
Solución
Las dos líneas están separadas por\(3 – (-5)\) unidades o con 8 unidades de diferencia.
Ejemplo\(\PageIndex{2}\)
Encuentra la distancia entre\(x=-5\) y\(x=-10\).
Solución
Las dos líneas están separadas por\(-5 – (-10)\) unidades, o 5 unidades de distancia.
Ejemplo\(\PageIndex{3}\)
Encuentra la distancia entre\(y=5\) y\(y=-8\).
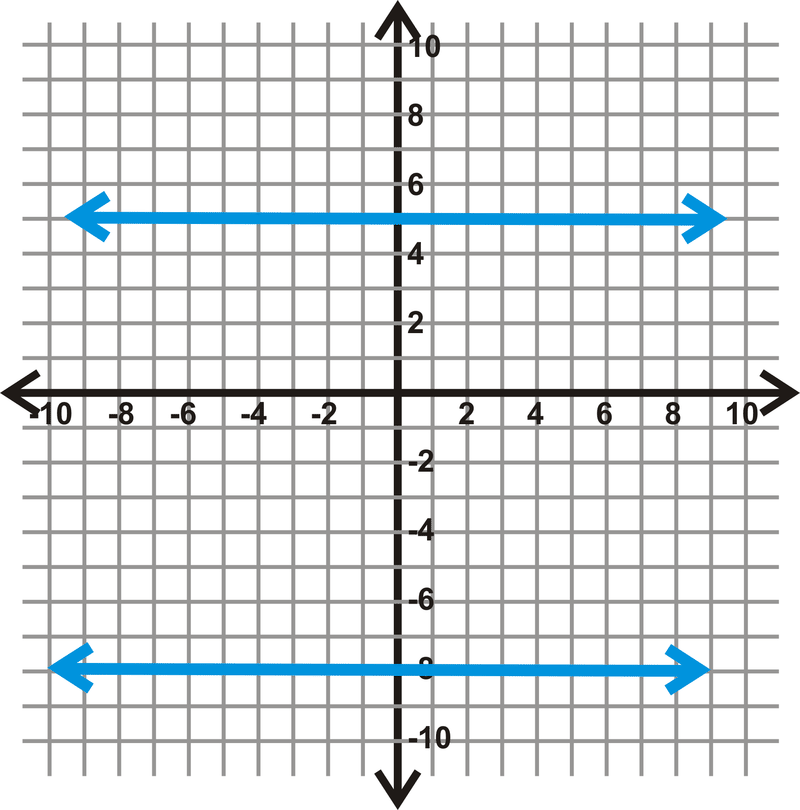
Solución
Las dos líneas están separadas por\(5 – (-8)\) unidades, o 13 unidades de diferencia.
Ejemplo\(\PageIndex{4}\)
Encuentra la distancia entre\(y=x+6\) y\(y=x−2\).
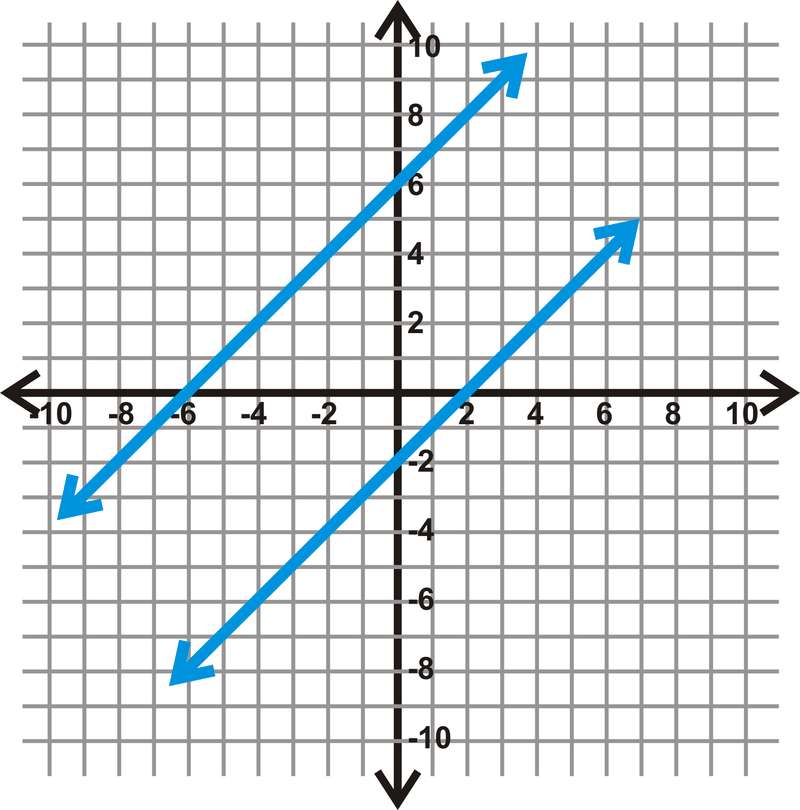
Solución
Paso 1: Encuentra la pendiente perpendicular.
\(m=1\), entonces\(m_{\perp} =-1\).
Paso 2: Encuentra la intersección y de la línea superior,\(y=x+6\).
El intercepto es\((0, 6)\).
Paso 3: Usa la pendiente y cuenta atrás 1 y a la derecha 1 hasta que golpees\(y=x−2\).
Siempre subir/ejecutar la misma cantidad para\(m=1\) o\(m=-1\).
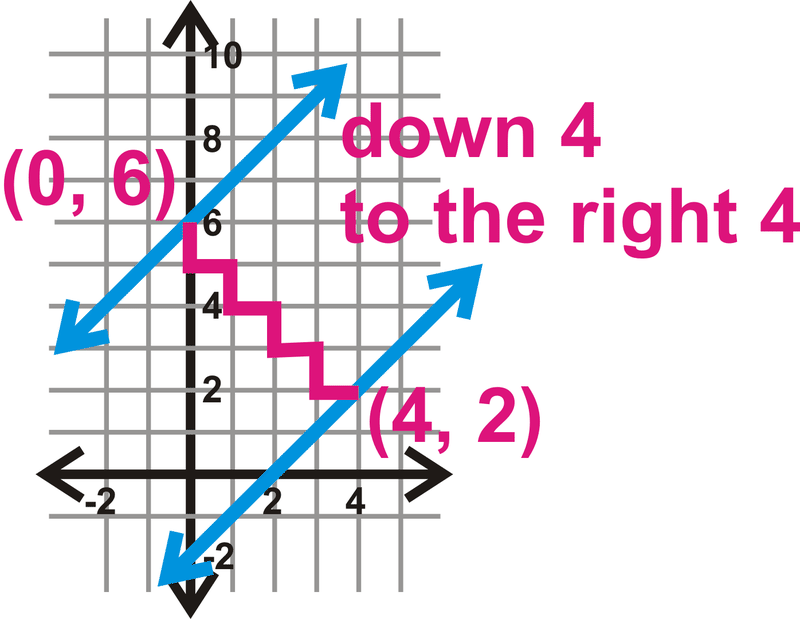
Paso 4: Usa estos dos puntos en la fórmula de distancia para determinar qué tan separadas están las líneas.
\(\begin{align*} d&=\sqrt{(0−4)^2+(6−2)^2} \\ &=\sqrt{(−4)^2+(4)^2} \\ &=\sqrt{16+16} \\ &=\sqrt{32}=5.66\: units\end{align*}\)
Ejemplo\(\PageIndex{5}\)
Encuentra la distancia entre\(y=-x−1\), y\(y=-x−3\).
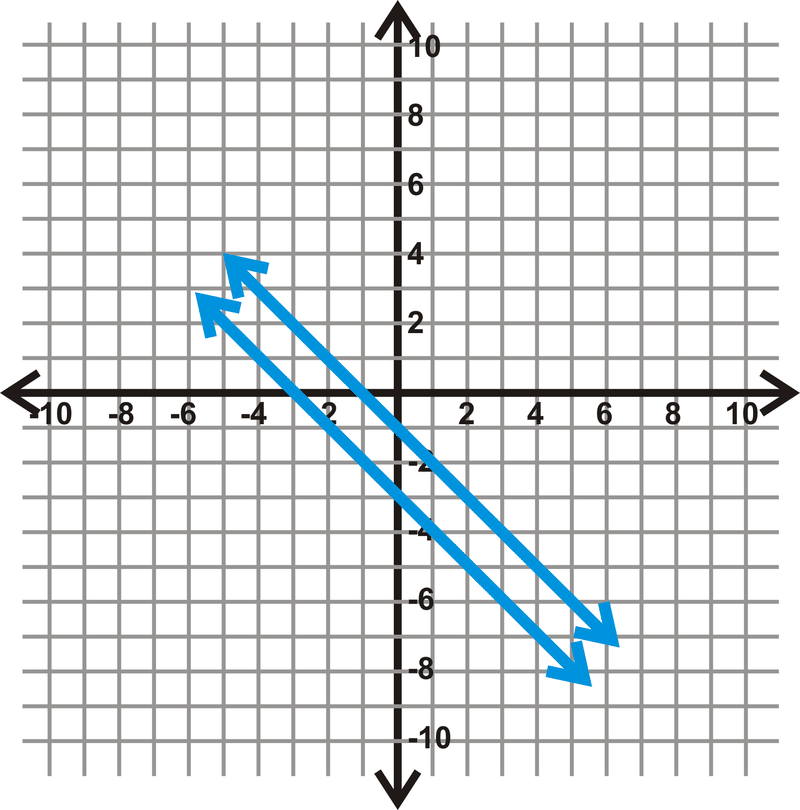
Solución
Paso 1: Encuentra la pendiente perpendicular.
\(m=-1\), entonces\(m_{\perp} =1\).
Paso 2: Encuentra la intersección y de la línea superior,\(y=-x−1\).
El intercepto es\((0, -1)\).
Paso 3: Usa la pendiente y cuenta atrás 1 y a la izquierda 1 hasta que golpees\(y=x−3\).
Paso 4: Usa estos dos puntos en la fórmula de distancia para determinar qué tan separadas están las líneas.
\(\begin{align*} d&=\sqrt{(0−(-1))^2+(-1−(-2))^2} \\ &=\sqrt{(1)^2+(1)^2} \\ &=\sqrt{1+1} \\ &=\sqrt{2}=1.41\: units \end{align*}\)
Revisar
Usa cada gráfica a continuación para determinar qué tan lejos está cada par de líneas paralelas.
-
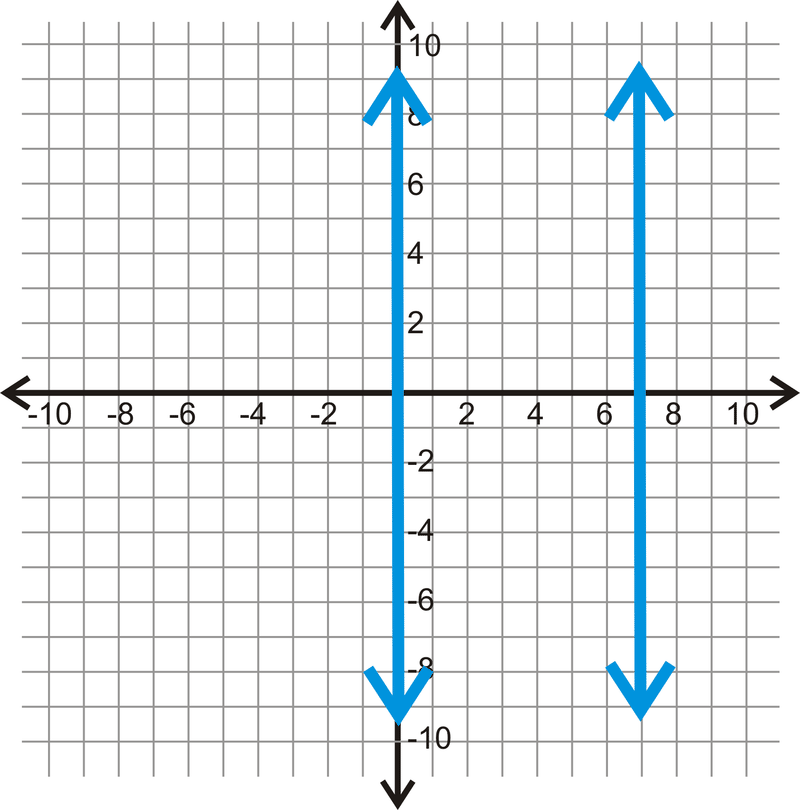
Figura\(\PageIndex{8}\) -
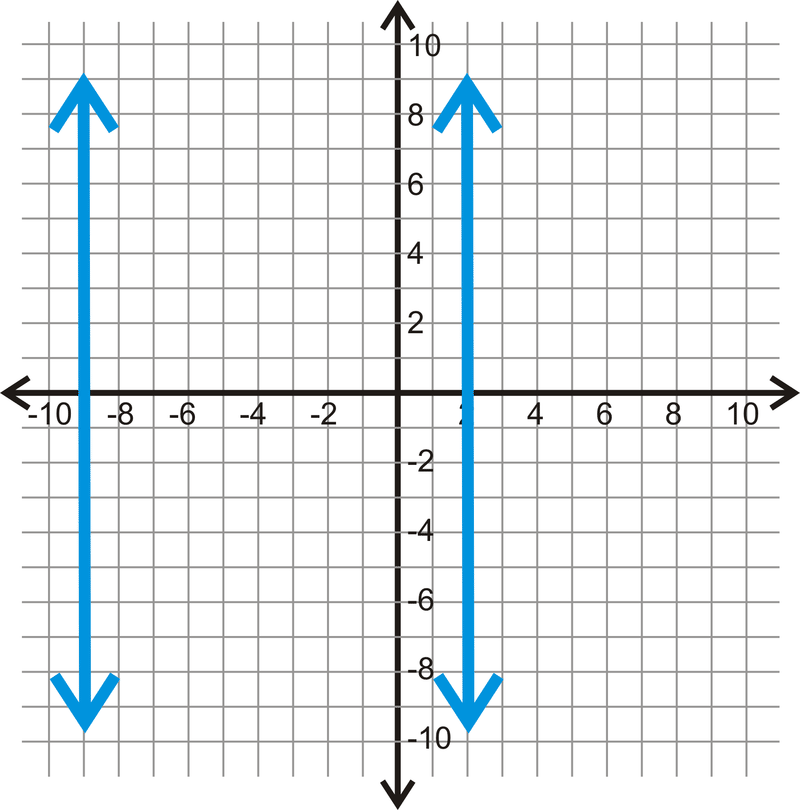
Figura\(\PageIndex{9}\) -
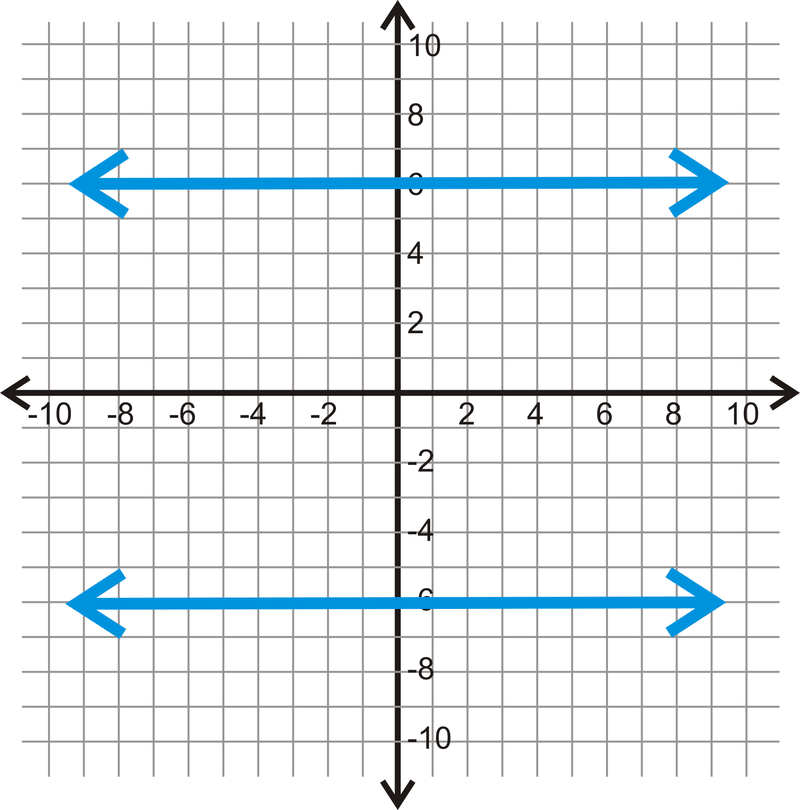
Figura\(\PageIndex{10}\) -
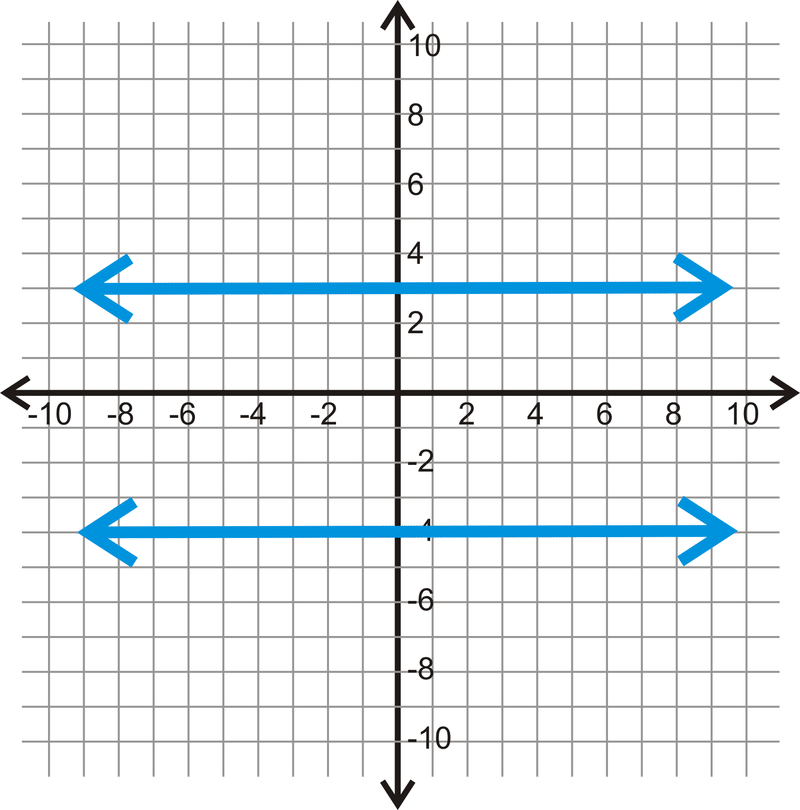
Figura\(\PageIndex{11}\)
Determinar la distancia más corta entre cada par de líneas paralelas. Redondee su respuesta a la centésima más cercana.
- \(x=5\),\(x=1\)
- \(y=−6\),\(y=4\)
- \(y=3\),\(y=15\)
- \(x=−10\),\(x=−1\)
- \(x=8\),\(x=0\)
- \(y=7\),\(y=−12\)
Encuentra la distancia entre las líneas paralelas dadas.
- \(y=x−3\),\(y=x+11\)
- \(y=−x+4\),\(y=−x\)
- \(y=−x−5\),\(y=−x+1\)
- \(y=x+12\),\(y=x−6\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 3.11.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Fórmula de distancia | La distancia entre dos puntos\((x_1,y_1)\) y se\((x_2,y_2)\) puede definir como\(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\). |
| perpendiculares | Las líneas perpendiculares son líneas que se cruzan en\(90^{\circ}\) ángulo. El producto de las pendientes de dos líneas perpendiculares es -1. |
Recursos adicionales
Elemento Interactivo
Video: Encontrar la distancia entre líneas paralelas Principios - Básico
Actividades: Distancia entre líneas paralelas Preguntas de discusión
Ayudas de estudio: Líneas en el plano de coordenadas
Práctica: Distancia entre líneas paralelas
Mundo real: Flipping Out