5.9: Paralelogramos
- Page ID
- 107499
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Encuentra medidas de ángulo desconocidas de cuadriláteros con dos pares de lados paralelos.
Un paralelogramo es un cuadrilátero con dos pares de lados paralelos.

Observe que cada par de lados está marcado paralelo (para las dos últimas formas, recuerde que cuando dos líneas son perpendiculares a la misma línea entonces son paralelas). Los paralelogramas tienen muchas propiedades interesantes.
Datos sobre los paralelogramos
- Teorema de lados opuestos: Si un cuadrilátero es un paralelogramo, entonces ambos pares de lados opuestos son congruentes.
Si
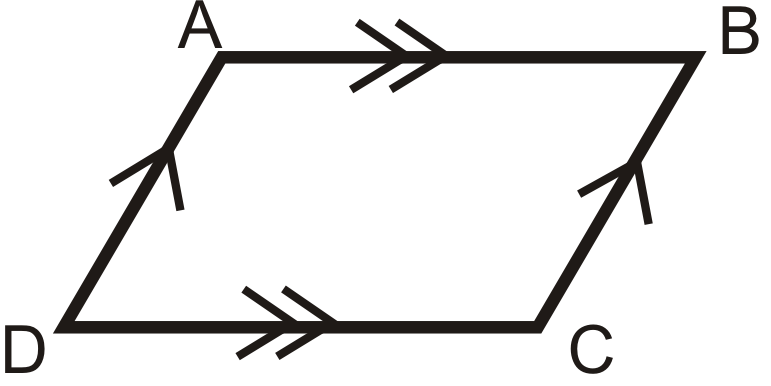
entonces
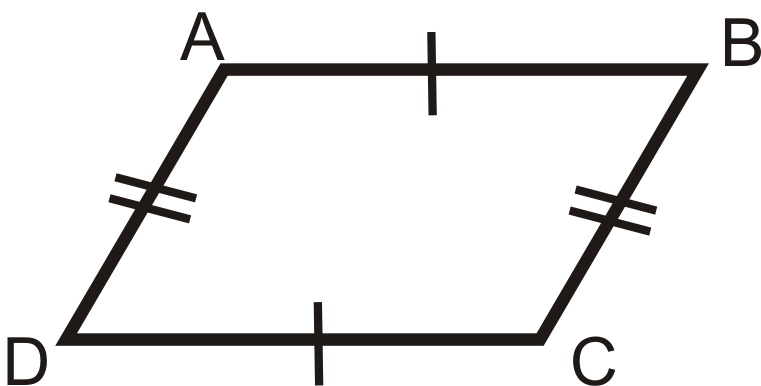
2. Teorema de ángulos opuestos: Si un cuadrilátero es un paralelogramo, entonces ambos pares de ángulos opuestos son congruentes.
Si
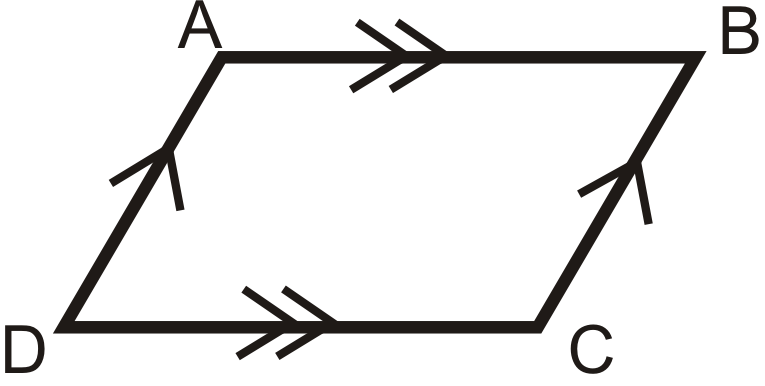
entonces
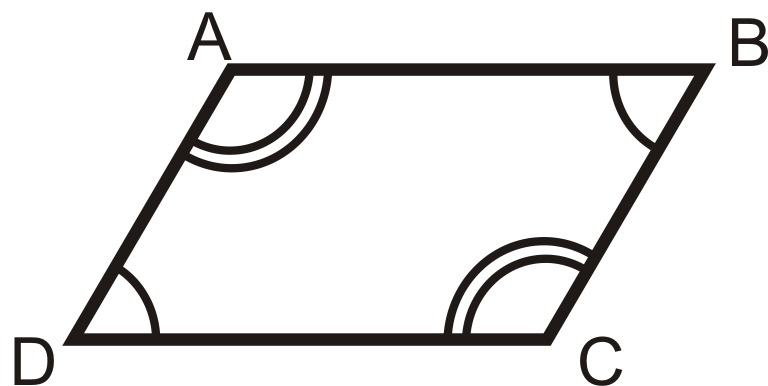
3. Teorema de ángulos consecutivos: Si un cuadrilátero es un paralelogramo, entonces todos los pares de ángulos consecutivos son complementarios.
Si

entonces

\(\begin{aligned} m\angle A+m\angle D&=180^{\circ} \\ m\angle A+m\angle B&=180^{\circ} \\ m\angle B+m\angle C&=180^{\circ} \\ m\angle C+m\angle D&=180^{\circ} \end{aligned}\)
4. Teorema de las diagonales del paralelogramo: Si un cuadrilátero es un paralelogramo, entonces las diagonales se bisecan entre sí.
Si

entonces
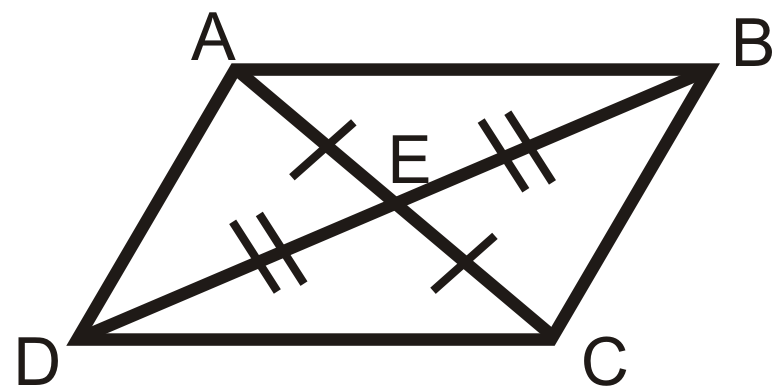
¿Y si te dijeran que\(FGHI\) es un paralelogramo y se te da la longitud de FG\) y la medida de\(\angle F\)? ¿Qué puedes determinar sobre\(HI\)\(\angle H\),\(\angle G\), y\(\angle I\)?
Ejemplo\(\PageIndex{1}\)
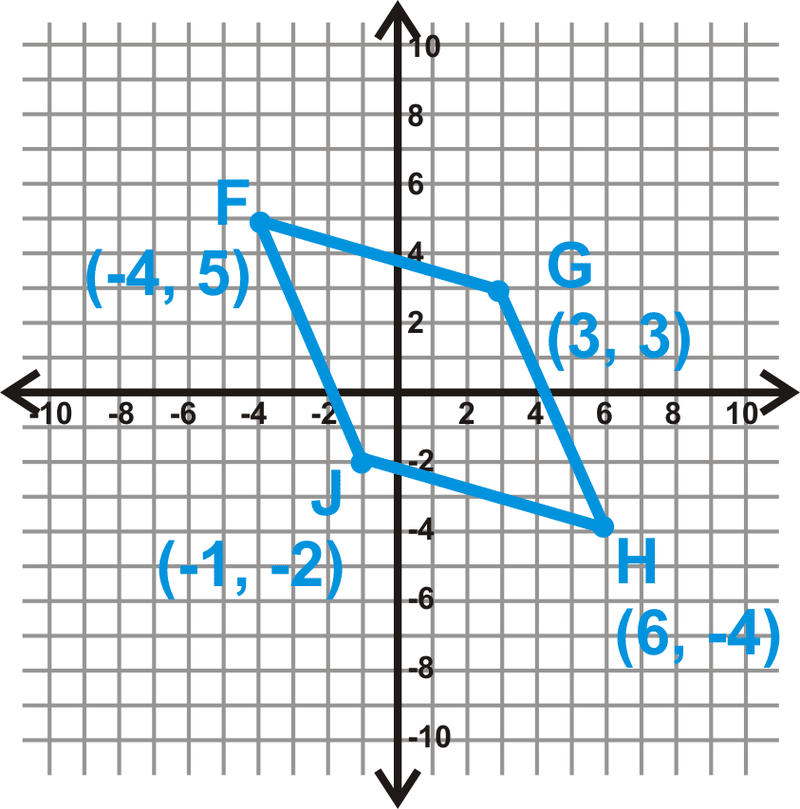
Demostrar que las diagonales de\(FGHJ\) bisectar entre sí.
Solución
Encuentra el punto medio de cada diagonal.
\(\begin{aligned}\text{ Midpoint of } \overline{FH}:& \left(\dfrac{−4+6}{2}, \dfrac{5−4}{2}\right)=(1,0.5) \\ \text{ Midpoint of } of\: \overline{GJ}: & \left(\dfrac{3−1}{2}, \dfrac{3−2}{2}\tight)=(1,0.5)\end{aligned}\)
Debido a que son el mismo punto, las diagonales se cruzan en el punto medio de la otra. Esto significa que se bisectan entre sí.
Ejemplo\(\PageIndex{2}\)
Encuentre las medidas de a y b en el paralelogramo a continuación:

Solución
Los ángulos consecutivos son suplementarios por lo\(127^{\circ}+m\angle b=180^{\circ}\) que significa que\(m\angle b=53^{\circ}\). \(a\)y\(b\) son ángulos interiores alternos y dado que las líneas son paralelas (ya que es un paralelogramo), eso significa que\(m\angle a=m\angle b=53^{\circ}\).
Ejemplo\(\PageIndex{3}\)
\(ABCD\)es un paralelogramo. Si\(m\angle A=56^{\circ}\), encuentra la medida de los otros ángulos.
Solución
Primero dibuja un cuadro. Al etiquetar los vértices, se listan las letras, en orden.
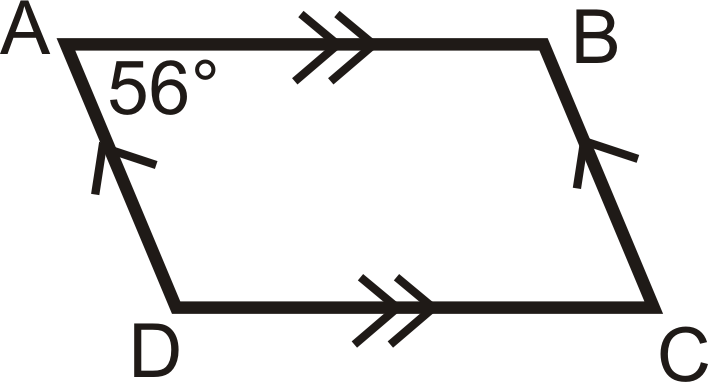
Si\(m\angle A=56^{\circ}\), entonces\(m\angle C=56^{\circ}\) por el Teorema de Ángulos Opuestos.
\ (\ begin {alineado}
&m\ ángulo A+m\ ángulo B=180^ {\ circ}\ quad\ text {por el Teorema de Ángulos Consecutivos.}\\
&56^ {\ circ} +m\ ángulo B=180^ {\ circ}\\
&m\ ángulo B=124^ {\ circ}\ quad m\ ángulo D=124^ {\ circ}\ quad\ text {porque es un ángulo opuesto a}\ ángulo B
\ end {alineado}\)
Ejemplo\(\PageIndex{4}\)
Encuentra los valores de\(x\) y\(y\).
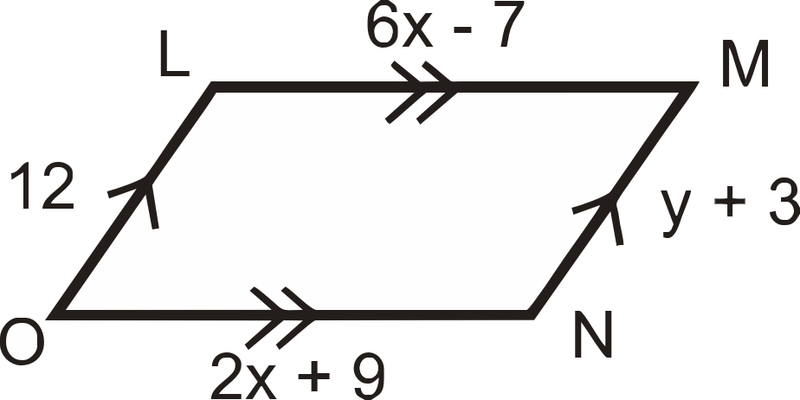
Solución
Recuerda que los lados opuestos de un paralelogramo son congruentes. Configura ecuaciones y resuelve.
\(\begin{aligned} 6x−7&=2x+9 \\ 4x&=16 \\ x&=4 \\ y+3&=12 \\ y&=9\end{aligned} \)
Ejemplo\(\PageIndex{5}\)
Demostrar el teorema de lados opuestos.

Solución
Dado:\(ABCD\) es un paralelogramo con diagonal\(\overline{BD}\)
Demostrar:\(\overline{AB}\cong \overline{DC}\),\(\overline{AD}\cong \overline{BC} \)
| Declaración | Razón |
|---|---|
| 1. \(ABCD\)es un paralelogramo con diagonal\(\overline{BD}\) | 1. Dado |
| 2. \(\overline{AB}\parallel \overline{DC}\),\(\overline{AD}\parallel \overline{BC}\) | 2. Definición de un paralelogramo |
| 3. \(\angle ABD\cong \angle BDC\),\(\angle ADB\cong \angle DBC\) | 3. Teorema de ángulos interiores alternos |
| 4. \(\overline{DB}\cong \overline{DB}\) | 4. PoC reflexivo |
| 5. \(\Delta ABD\cong \Delta CDB\) | 5. ASA |
| 6. \(\overline{AB}\cong \overline{DC}\),\(\overline{AD}\cong \overline{BC}\) | 6. CPCTC |
La prueba del Teorema de Ángulos Opuestos es casi idéntica.
Revisar
\(ABCD\)es un paralelogramo. Rellena los espacios en blanco a continuación.
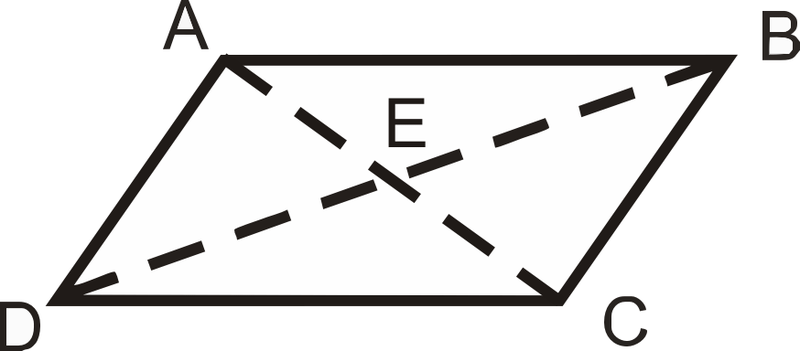
- Si\(AB=6\), entonces\(CD= \text{______}\).
- Si\(AE=4\), entonces\(AC= \text{______}\).
- Si\(m\angle ADC=80^{\circ}\),\(m\angle DAB = \text{______}\).
- Si\(m\angle BAC=45^{\circ}\),\(m\angle ACD = \text{______}\).
- Si\(m\angle CBD=62^{\circ}\),\(m\angle ADB = \text{______}\).
- Si\(DB=16\), entonces\(DE = \text{______}\).
- Si\( m\angle B=72^{\circ}\) en paralelogramo\(ABCD\), encuentra los otros tres ángulos.
- Si\(m\angle S=143^{\circ}\) en paralelogramo\(PQRS\), encuentra los otros tres ángulos.
- Si está\(\overline{AB}\perp \overline{BC}\) en paralelogramo\(ABCD\), encuentre la medida de los cuatro ángulos.
- Si\(m\angle F=x^{\circ}\) en paralelogramo\(EFGH\), encuentra los otros tres ángulos.
Para las preguntas 11-18, encuentre los valores de la (s) variable (s). Todas las cifras a continuación son paralelogramos.
-
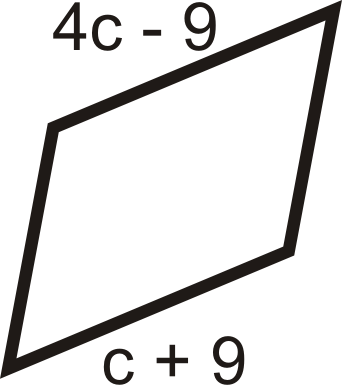
Figura\(\PageIndex{16}\) -
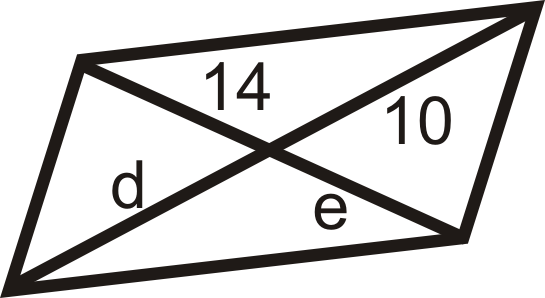
Figura\(\PageIndex{17}\) -
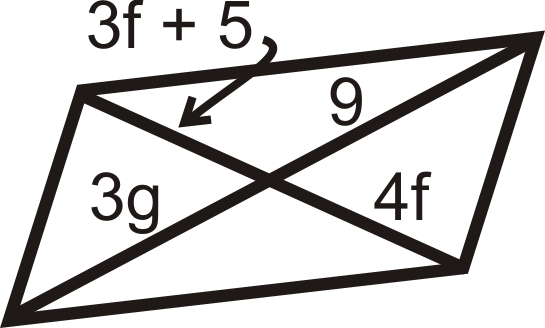
Figura\(\PageIndex{18}\) -
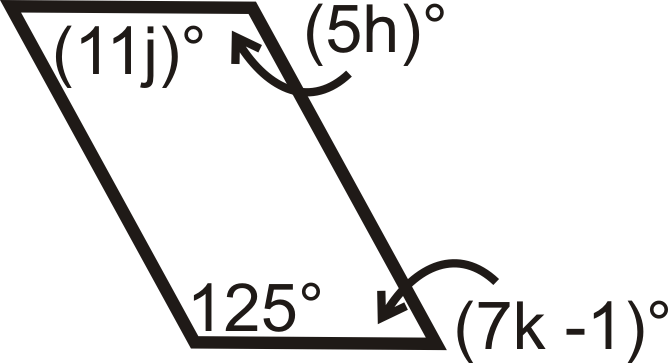
Figura\(\PageIndex{19}\) -
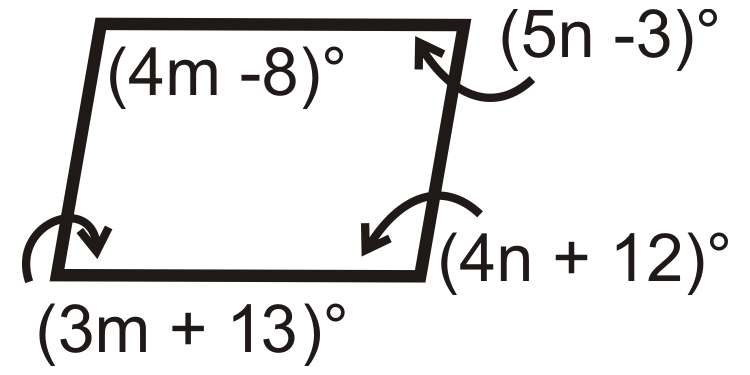
Figura\(\PageIndex{20}\) -
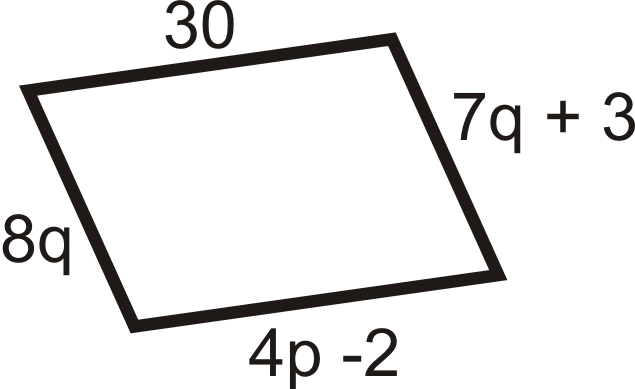
Figura\(\PageIndex{21}\) -
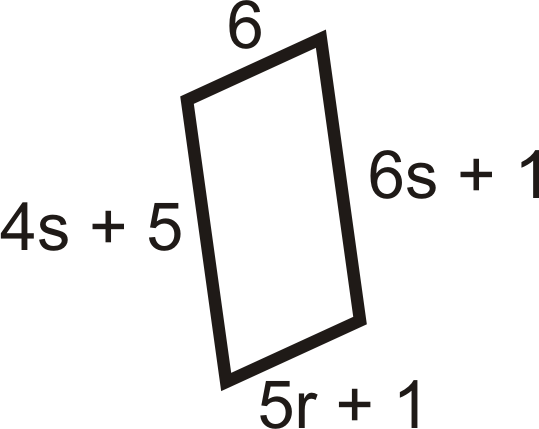
Figura\(\PageIndex{22}\) -
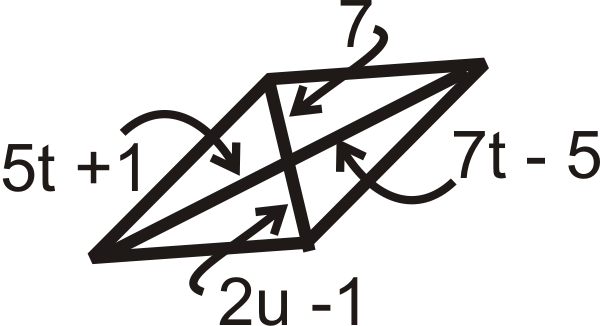
Figura\(\PageIndex{23}\)
Usa el paralelogramo\(WAVE\) para encontrar:
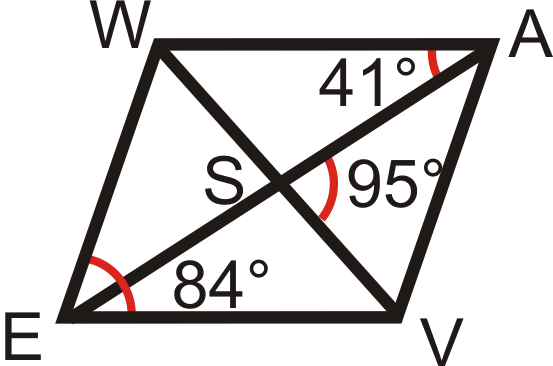
- \(m\angle AWE\)
- \(m\angle ESV\)
- \(m\angle WEA\)
- \(m\angle AVW\)
Encuentra el punto de intersección de las diagonales para ver si\(EFGH\) es un paralelogramo.
- \(E(−1,3), F(3,4), G(5,−1), H(1,−2)\)
- \(E(3,−2), F(7,0), G(9,−4), H(5,−4)\)
- \(E(−6,3), F(2,5), G(6,−3), H(−4,−5)\)
- \(E(−2,−2), F(−4,−6), G(−6,−4), H(−4,0)\)
Rellene los espacios en blanco en las pruebas a continuación.
- Teorema de ángulos opuestos

Dado:\(ABCD\) es un paralelogramo con diagonal\(\overline{BD}\)
Demostrar:\(\angle A\cong \angle C\)
| Declaración | Razón |
|---|---|
| 1. | 1. Dado |
| 2. \(\overline{AB}\parallel \overline{DC}\),\(\overline{AD}\parallel \overline{BC}\) | 2. |
| 3. | 3. Teorema de ángulos interiores alternos |
| 4. | 4. PoC reflexivo |
| 5. \(\Delta ABD\cong \Delta CDB\) | 5. |
| 6. \(\angle A\cong \angle C\) | 6. |
- Teorema de las diagonales del paralelogramo

Dado:\(ABCD\) es un paralelogramo con diagonales\(\overline{BD}\) y\(\overline{AC}\)
Demostrar:\(\overline{AE}\cong \overline{EC}\),\(\overline{DE}\cong \overline{EB}\)
| Declaración | Razón |
|---|---|
| 1. | 1. |
| 2. | 2. Definición de un paralelogramo |
| 3. | 3. Teorema de ángulos interiores alternos |
| 4. \(\overline{AB}\cong \overline{DC}\) | 4. |
| 5. | 5. |
| 6. \( \overline{AE}\cong \overline{EC}\),\(\overline{DE}\cong \overline{EB}\) | 6. |
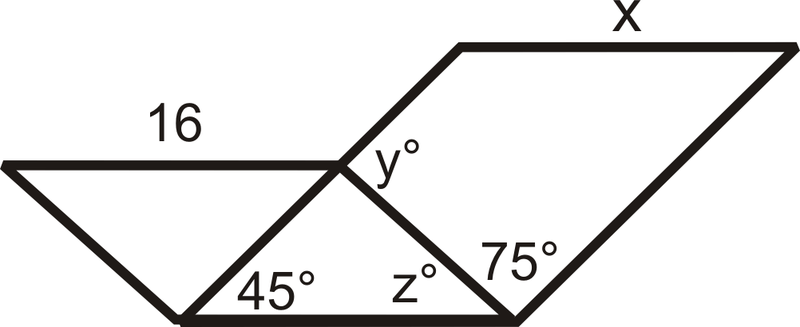
- Encontrar\(x\),\(y^{\circ}\), y\(z^{\circ}\). (Los dos cuadriláteros con el mismo lado son paralelogramos.)
El vocabulario
| Término | Definición |
|---|---|
| paralelogramo | Un cuadrilátero con dos pares de lados paralelos. Un paralelogramo puede ser un rectángulo, un rombo o un cuadrado, pero no necesita ser ninguno de los tres. |
Recursos adicionales
Elemento Interactivo
Video: Principios de paralelogramos - Básico
Actividades: Paralelogramas Preguntas de Discusión
Ayudas de estudio: Guía de estudio de paralelogramos
Práctica: Paralelogramos
Mundo Real: Paralelogramos

