6.20: Teorema de la Secante Tangente
- Page ID
- 107250
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Producto del segmento exterior y secante entera equivale al cuadrado de la tangente al mismo punto.
Segmentos de Secantes y Tangentes
Si una tangente y una secante se encuentran en un punto común fuera de un círculo, los segmentos creados tienen una relación similar a la de dos rayos secantes.
Teorema de Segmento Secante Tangente: Si una tangente y una secante se dibujan a partir de un punto común fuera del círculo (y los segmentos se etiquetan como la imagen de abajo), entonces\(a^2=b(b+c)\).
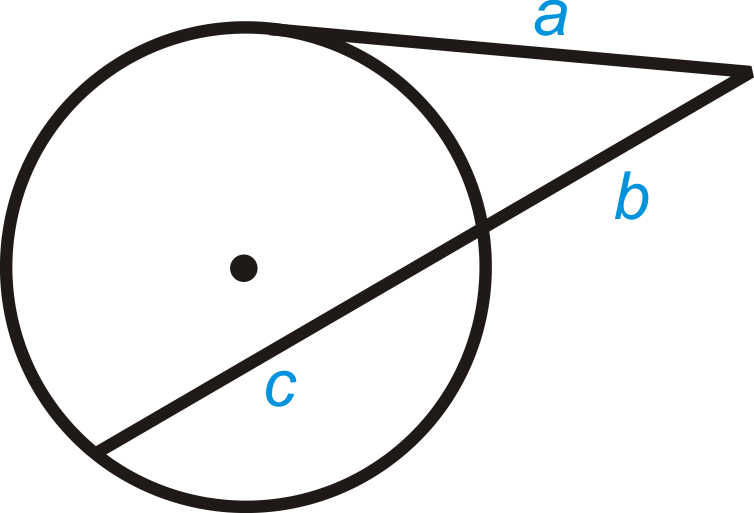
¿Y si te dieran un círculo con una tangente y una secante que se cruzan fuera del círculo? ¿Cómo podría usar la longitud de algunos de los segmentos formados por su intersección para determinar las longitudes de los segmentos desconocidos?
Ejemplo\(\PageIndex{1}\)
Encuentra\(x\). Simplifica cualquier tipo de radicales.
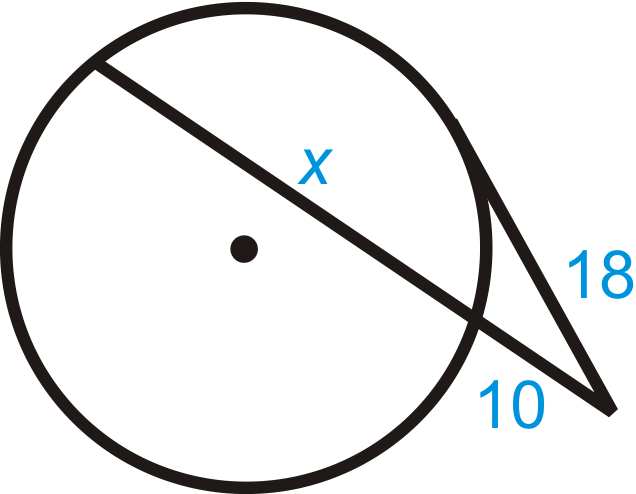
Solución
Utilice el Teorema del Segmento Secante Tangente.
\(\begin{aligned} 18^2&=10(10+x) \\ 324&=100+10x \\ 224&=10x \\ x&=22.4\end{aligned}\)
Ejemplo\(\PageIndex{2}\)
Encuentra\(x\). Simplifica cualquier tipo de radicales.
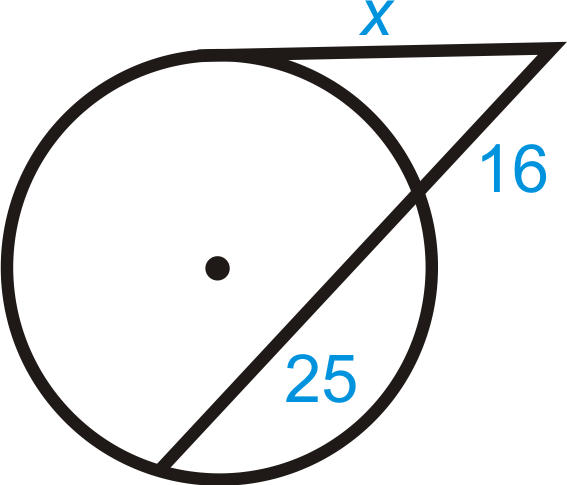
Solución
Utilice el Teorema del Segmento Secante Tangente.
\(\begin{aligned} x^2&=16(16+25) \\ x^2&=656 \\ x&=4\sqrt{41}\end{aligned}\)
Ejemplo\(\PageIndex{3}\)
Encuentra la longitud del segmento faltante.
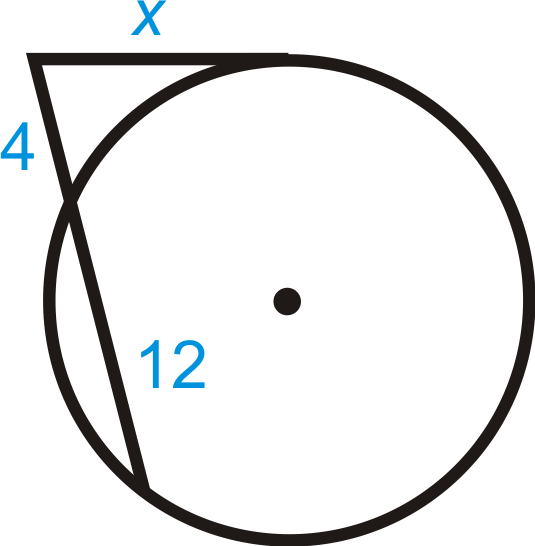
Solución
Utilice el Teorema del Segmento Secante Tangente.
\(\begin{aligned} x^2&=4(4+12) \\ x^2&=4\cdot 16=64 \\ x&=8\end{aligned}\)
Ejemplo\(\PageIndex{4}\)
Rellene el espacio en blanco y luego resuelva el segmento faltante.
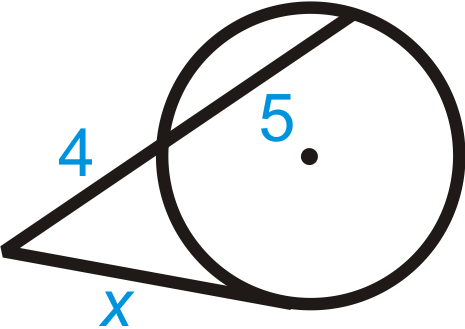
Solución
\(\text{______}=\text{______}(4+5)\)
\(\begin{aligned} x^2&=4(4+5) \\ x^2&=36 \\ x&=6\end{aligned}\)
Ejemplo\(\PageIndex{5}\)
Encuentra el valor del segmento faltante.
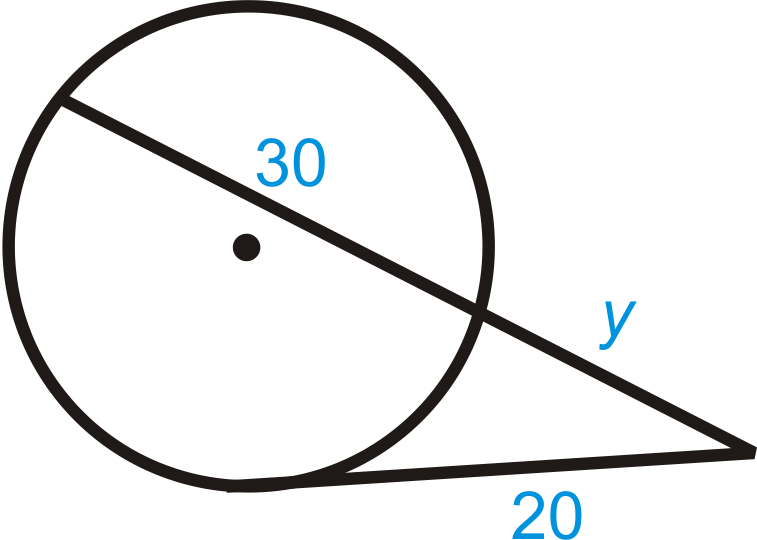
Solución
Utilice el Teorema del Segmento Secante Tangente.
\(\begin{aligned} 20^2&=y(y+30) \\ 400&=y^2+30y \\ 0&=y^2+30y−400 \\ 0&=(y+40)(y−10) \\ y&=\xcancel{−40},10 \end{aligned}\)
Revisar
Rellene los espacios en blanco para cada problema a continuación y luego resuelva el segmento faltante.
-
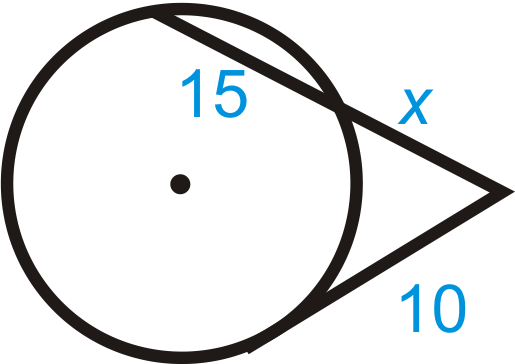
Figura\(\PageIndex{7}\)
\(10^2=x(\text{______}+\text{______})\)
Encuentra\(x\) en cada diagrama a continuación. Simplifica cualquier tipo de radicales.
-
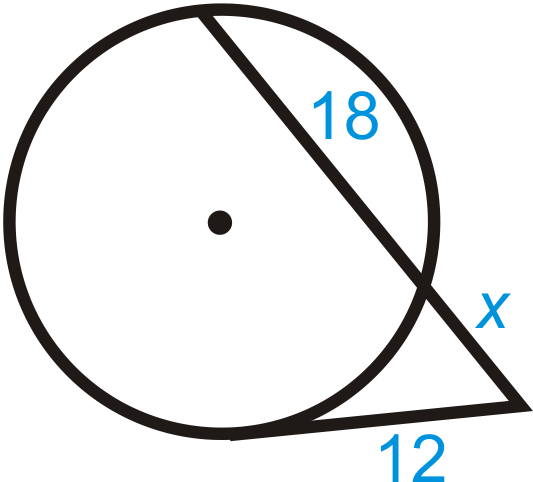
Figura\(\PageIndex{8}\) -
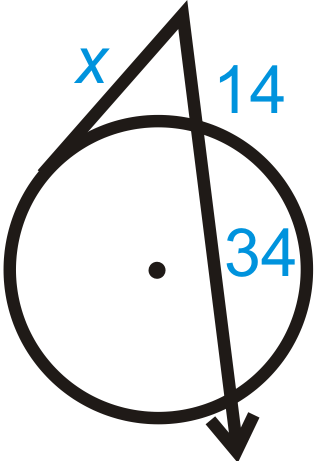
Figura\(\PageIndex{9}\) -
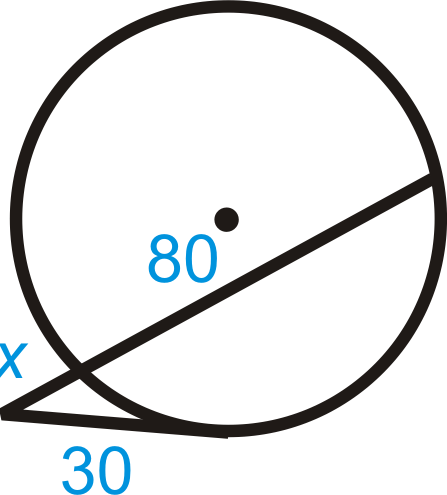
Figura\(\PageIndex{10}\) - Describir y corregir el error en la búsqueda\(y\).
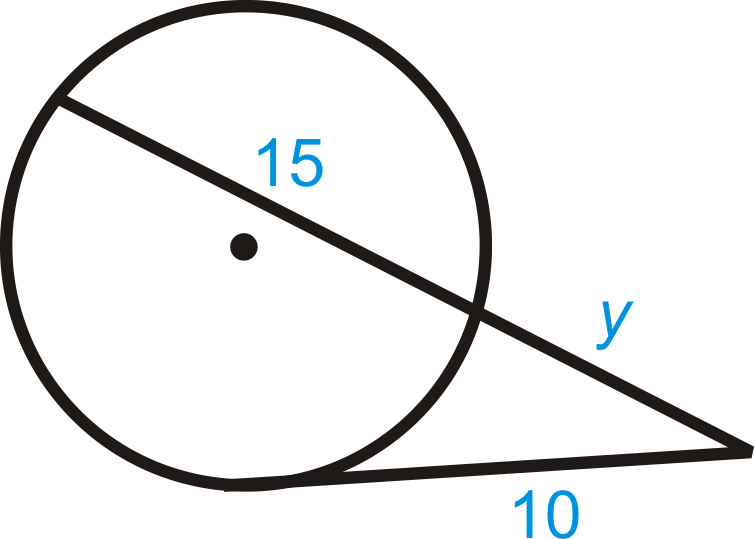
Figura\(\PageIndex{11}\)
\(\begin{aligned} 10\cdot 10&=y\cdot 15y \\ 100&=15y^2 \\ \dfrac{20}{3}&=y^2 \\ \dfrac{2\sqrt{15}}{3}&=y \color{red} \leftarrow \text{y is \underline{not} correct}\end{aligned}\)
Resolver para la variable desconocida.
-
Figura\(\PageIndex{12}\) -
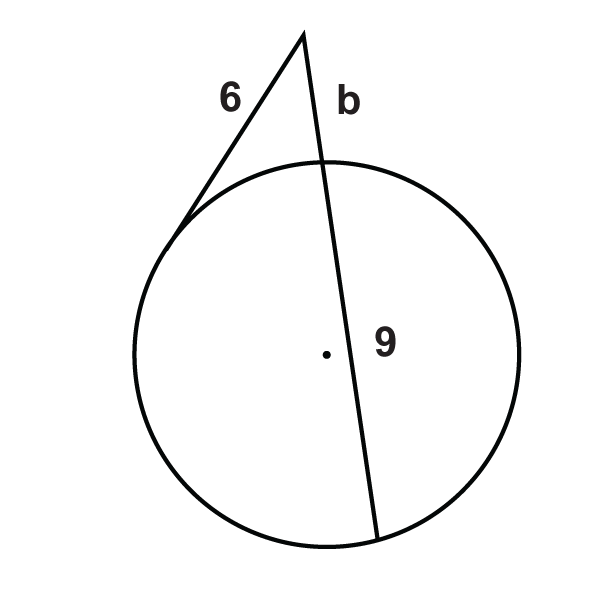
Figura\(\PageIndex{13}\) -
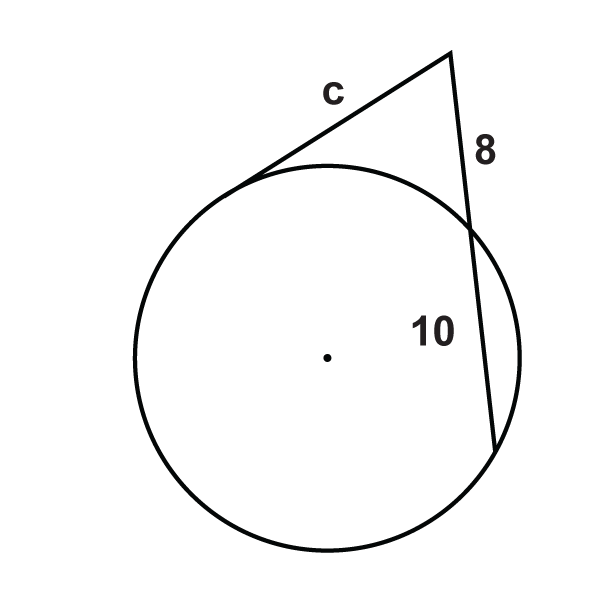
Figura\(\PageIndex{14}\) -
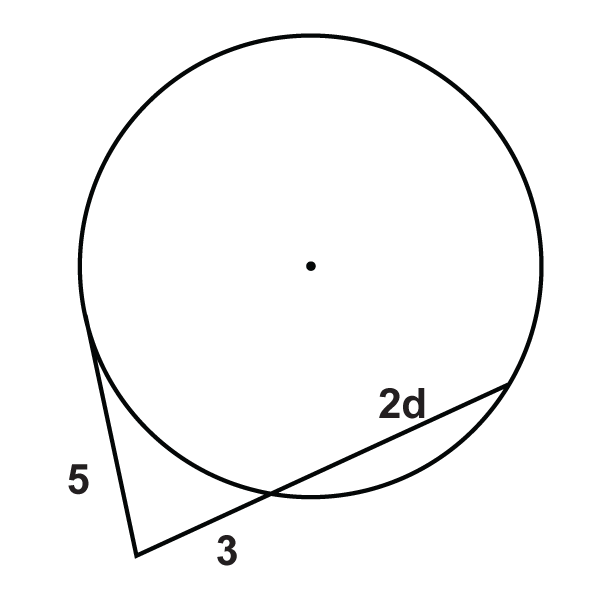
Figura\(\PageIndex{15}\) -
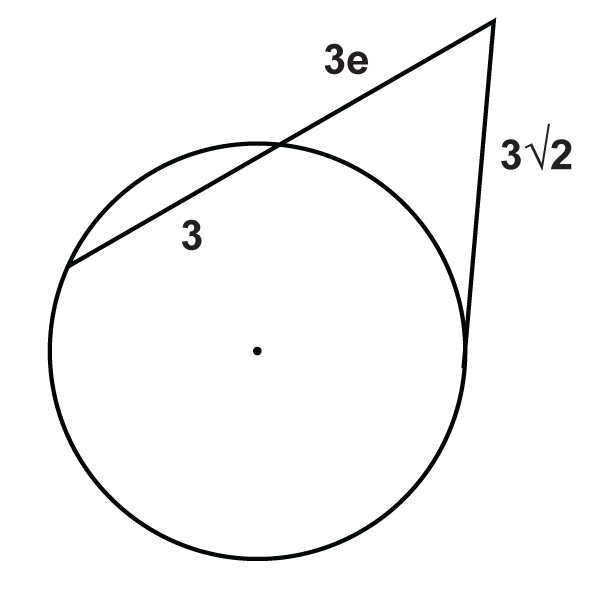
Figura\(\PageIndex{16}\) -
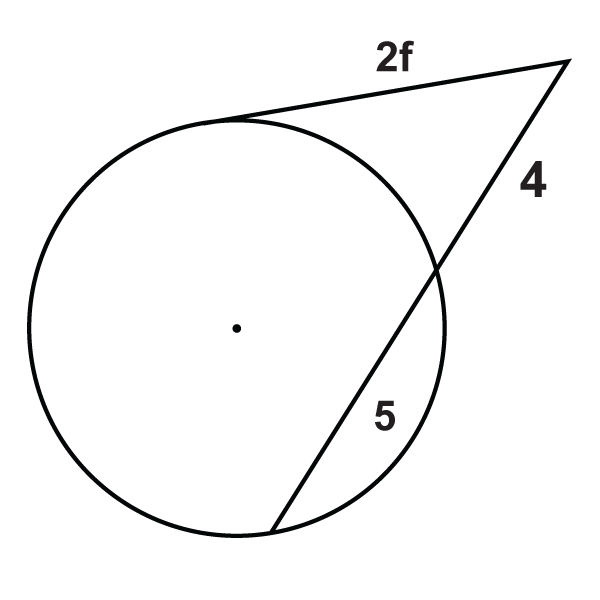
Figura\(\PageIndex{17}\) -
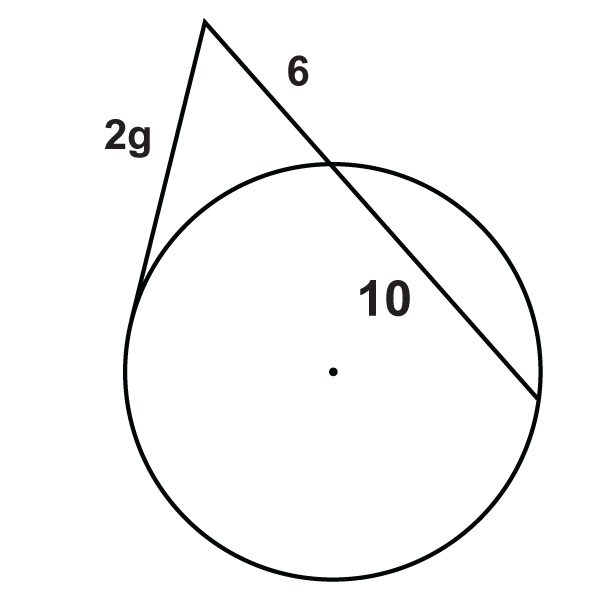
Figura\(\PageIndex{18}\) -
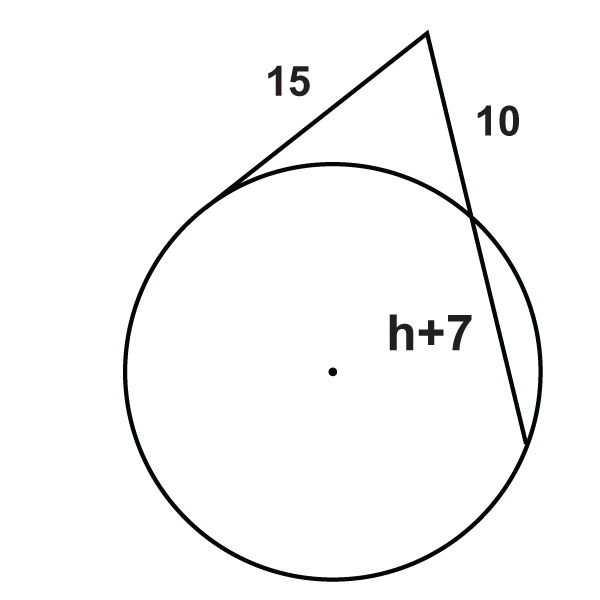
Figura\(\PageIndex{19}\) -
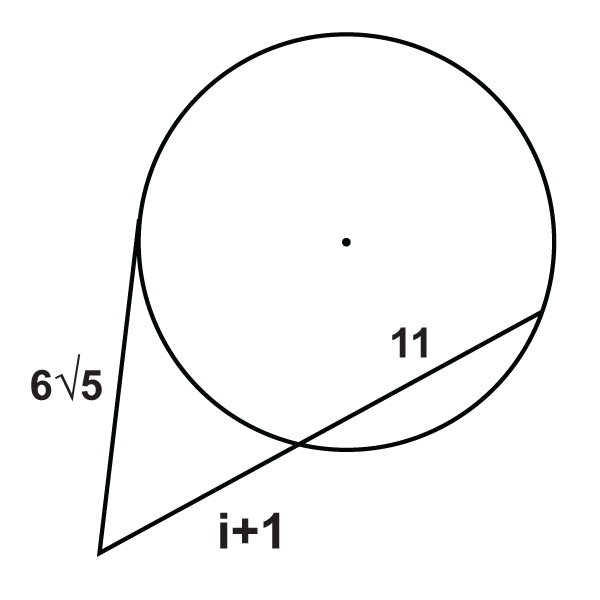
Figura\(\PageIndex{20}\) -
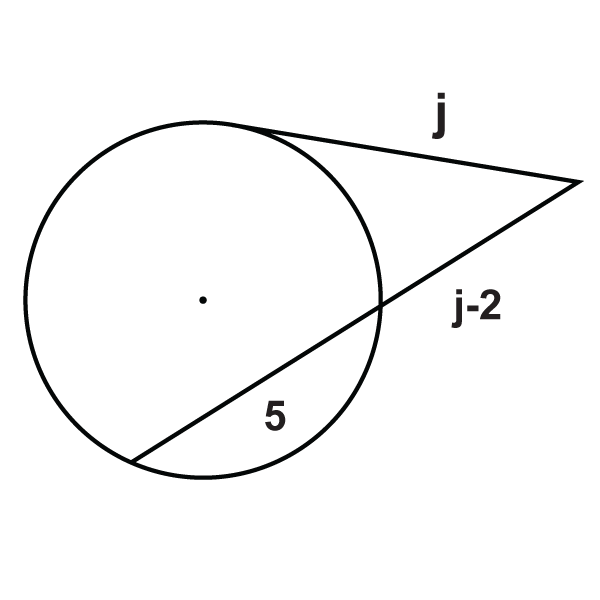
Figura\(\PageIndex{21}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.11.
El vocabulario
| Término | Definición |
|---|---|
| ángulo central | Un ángulo formado por dos radios y cuyo vértice se encuentra en el centro del círculo. |
| acorde | Un segmento de línea cuyos extremos están en un círculo. |
| círculo | El conjunto de todos los puntos que están a la misma distancia de un punto específico, llamado el centro. |
| diámetro | Un acorde que pasa por el centro del círculo. La longitud de un diámetro es dos veces la longitud de un radio. |
| ángulo inscrito | Un ángulo con su vértice en el círculo y cuyos lados son acordes. |
| arco interceptado | El arco que se encuentra dentro de un ángulo inscrito y cuyos extremos están en el ángulo. |
| punto de tangencia | El punto donde la línea tangente toca el círculo. |
| radio | La distancia desde el centro hasta el borde exterior de un círculo. |
| Secante | La secante de un ángulo en un triángulo rectángulo es el valor que se encuentra dividiendo la longitud de la hipotenusa por la longitud del lado adyacente al ángulo dado. La relación secante es la recíproca de la relación coseno. |
| Teorema de Tangentes Segmentos Secantes | Si una tangente y una secante se dibujan a partir de un punto común fuera del círculo (y los segmentos se etiquetan como la imagen de abajo), entonces\(a^2 = b(b+c)\). |
Recursos adicionales
Elemento Interactivo
Actividades: Segmentos de Secantes y Tangentes Preguntas de Discusión
Ayudas de estudio: Círculos: Segmentos y longitudes Guía de estudio
Práctica: Teorema de la Secante Tangente