7.1: Cifras similares
- Page ID
- 107421
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Figuras que tienen la misma forma pero no el mismo tamaño.
Identificación de Triángulos como Similares, Congruentes o Ninguno

Gabriel está en geometría. Utiliza diferentes herramientas para medir diferentes artículos. Un día sienta un par de sus herramientas juntos y se da cuenta de que dos de sus herramientas son triángulos. Su clase ha comparado recientemente triángulos y los ha identificado como similares, congruentes o ninguno. Se supone que la clase debe estar usando sus herramientas de medición para medir elementos alrededor del aula y determinar si son similares, congruentes o ninguno. Gabriel echa un buen vistazo a las dos formas luego decide identificarlas para que pueda agregarlas a su lista. ¿Los triángulos de Gabriel son similares, congruentes o ninguno?
En este concepto, aprenderás a distinguir entre triángulos.
Identificar triángulos como Similares, Congruentes o Ninguno
Congruente significa ser exactamente lo mismo. Cuando dos segmentos de línea tienen la misma longitud, son congruentes. Cuando dos figuras tienen la misma forma y tamaño, son congruentes.

Estos dos triángulos son congruentes. Son exactamente iguales en todos los sentidos. Son del mismo tamaño y la misma forma. Sus longitudes laterales son las mismas y que sus medidas de ángulo son las mismas.
En ocasiones, dos cifras serán similares. Similar significa que las figuras tienen la misma forma, pero no el mismo tamaño. Cifras similares no son congruentes.

Estos dos triángulos son similares. Tienen la misma forma, pero no son del mismo tamaño.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Gabriel y sus herramientas de medición.
Se da cuenta de que dos de sus herramientas son triángulos. ¿Sus triángulos son similares, congruentes o ninguno?
Solución
Primero, comprueba si los triángulos son del mismo tamaño.
No
A continuación, comprueba si los triángulos son de la misma forma.
No
Después, identificar los triángulos.
La respuesta es que los triángulos no son similares, ni congruentes. Gabriel enumerará los triángulos como ninguno.
Ejemplo\(\PageIndex{2}\)
Identificar los siguientes triángulos como similares, congruentes o ninguno.
Solución
Primero, comprueba si los triángulos tienen el mismo tamaño.
Sí
A continuación, comprueba si los triángulos tienen la misma forma.
Sí
Después, identificar los triángulos.
Congruente
La respuesta es que los triángulos son congruentes.
Ejemplo\(\PageIndex{3}\)
Identificar los siguientes triángulos como similares, congruentes, o ninguno.

Solución
Primero, comprueba si los triángulos son del mismo tamaño.
No
A continuación, comprueba si los triángulos son de la misma forma.
No
Después, identificar los triángulos.
Ni congruente, ni similar
La respuesta es que los triángulos no son congruentes, ni similares.
Ejemplo\(\PageIndex{4}\)
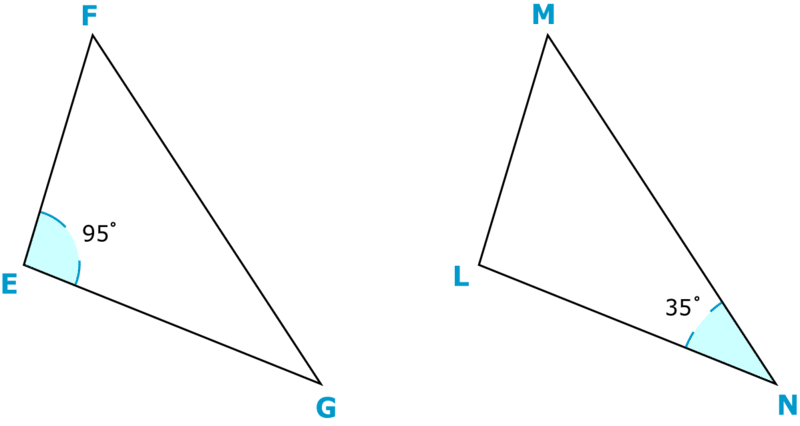
Identificar los siguientes triángulos como similares, congruentes, o ninguno.

Solución
Primero, comprueba si los triángulos son del mismo tamaño.
No
A continuación, comprueba si los triángulos son de la misma forma.
Sí
Después, identificar los triángulos.
Similares
La respuesta es que los triángulos son similares.
Ejemplo\(\PageIndex{5}\)
Identificar los siguientes triángulos como similares, congruentes, o ninguno.

Solución
Primero, comprueba si los triángulos son del mismo tamaño.
Sí
A continuación, comprueba si los triángulos son de la misma forma.
Sí
Después, identificar los triángulos.
Congruente
La respuesta es que los triángulos son congruentes.
Revisar
Identificar los triángulos dados como visualmente similares, congruentes o ninguno.
-

Figura\(\PageIndex{8}\) -

Figura\(\PageIndex{9}\) -

Figura\(\PageIndex{10}\) -

Figura\(\PageIndex{11}\) -

Figura\(\PageIndex{12}\)
Responde a cada una de las siguientes preguntas.
- Triángulos\(ABC\) y\(DEF\) son congruentes. ¿Significa esto que sus medidas de ángulo son las mismas? ¿Por qué?
- Verdadero o falso. Si los triángulos\(DEF\) y\(GHI\) son similares, entonces las longitudes laterales son diferentes pero las medidas del ángulo son las mismas.
- Verdadero o falso. Figuras similares tienen exactamente el mismo tamaño y forma.
- Verdadero o falso. Las cifras congruentes son exactamente las mismas en todos los sentidos.
- Triángulos\(LMN\) y\(HIJ\) son similares. Si esto es cierto, entonces las longitudes laterales son las mismas, verdaderas o falsas.
- Verdadero o falso. Para averiguar si dos figuras son similares, entonces sus longitudes laterales forman una proporción.
- Definir figuras similares
- Definir figuras congruentes.
- Usa una regla para dibujar un par congruente de triángulos.
- Usa una regla para dibujar un par de triángulos que sean similares.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.15.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| Similares | Dos figuras son similares si tienen la misma forma, pero no necesariamente del mismo tamaño. |
Recursos adicionales
Elemento interactivo
Video: Triángulos Congruentes y Similares - KA
Práctica: Cifras similares

