7.7: Similaridad AA

Dos triángulos son similares si dos pares de ángulos son congruentes.

Postulado de similitud AA

Por definición, dos triángulos son similares si todos sus ángulos correspondientes son congruentes y sus lados correspondientes son proporcionales. No es necesario revisar todos los ángulos y lados para saber si dos triángulos son similares. De hecho, si sólo se sabe que dos pares de ángulos correspondientes son congruentes es suficiente información para saber que los triángulos son similares. A esto se le llama Postulado de Similitud AA.

Postulado de similitud AA: Si dos ángulos en un triángulo son congruentes con dos ángulos en otro triángulo, entonces los dos triángulos son similares.

Figura$\PageIndex{1}$

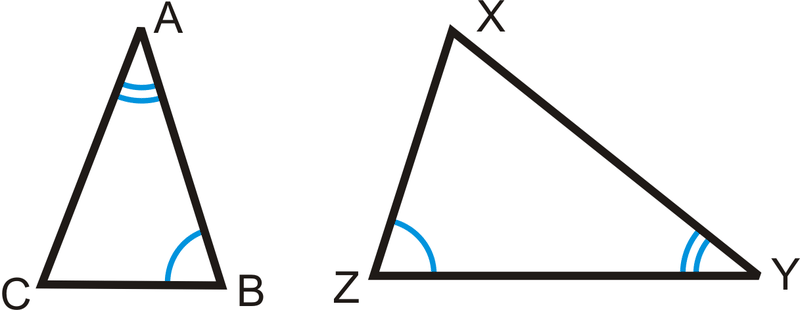
Si$\angle A\cong \angle Y$ y$\angle B\cong \angle Z$, entonces$\Delta ABC\sim \Delta YZX$.

¿Y si te dieran un par de triángulos y el ángulo mide para dos de sus ángulos? ¿Cómo podría usar esta información para determinar si los dos triángulos son similares?

Ejemplo$\PageIndex{1}$

¿Los triángulos son similares? Si es así, escriba una declaración de similitud.

Figura$\PageIndex{2}$

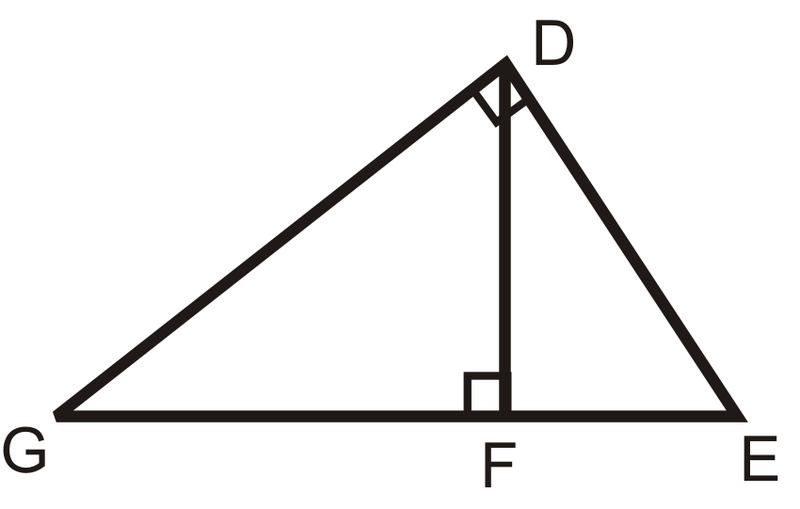
Solución

Sí, hay tres triángulos similares que tienen cada uno un ángulo recto. $DGE\sim FGD\sim FDE$.

Ejemplo$\PageIndex{2}$

¿Los triángulos son similares? Si es así, escriba una declaración de similitud.

Figura$\PageIndex{3}$

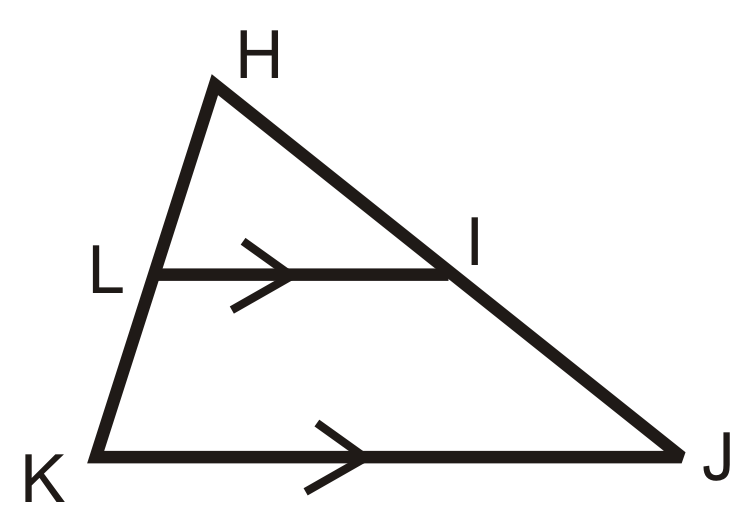
Solución

Por la propiedad reflexiva,$\angle H\cong \angle H$. Porque las líneas horizontales son paralelas,$\angle L\cong \angle K$ (ángulos correspondientes). Entonces sí, hay un par de triángulos similares. $HLI\sim HKJ$.

Ejemplo$\PageIndex{3}$

Determinar si los siguientes dos triángulos son similares. Si es así, escriba la declaración de similitud.

Figura$\PageIndex{4}$

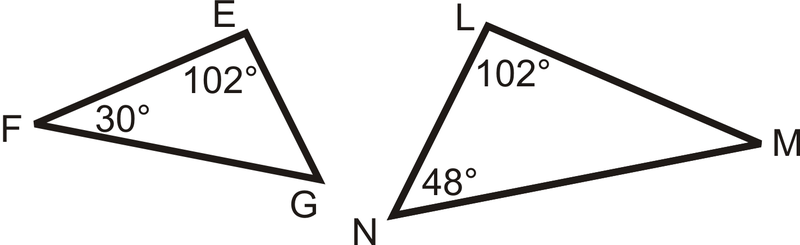
Solución

Compara los ángulos para ver si podemos usar el Postulado de Similitud AA. Usando el teorema de la suma del triángulo,$m\angle G=48^{\circ}$ y$m\angle M=30^{\circ}$. Entonces,$\angle F\cong \angle M$,$\angle E\cong \angle L$ y$\angle G\cong \angle N$ y los triángulos son similares. $\Delta FEG\sim \Delta MLN$.

Ejemplo$\PageIndex{4}$

Determinar si los siguientes dos triángulos son similares. Si es así, escriba la declaración de similitud.

Figura$\PageIndex{5}$

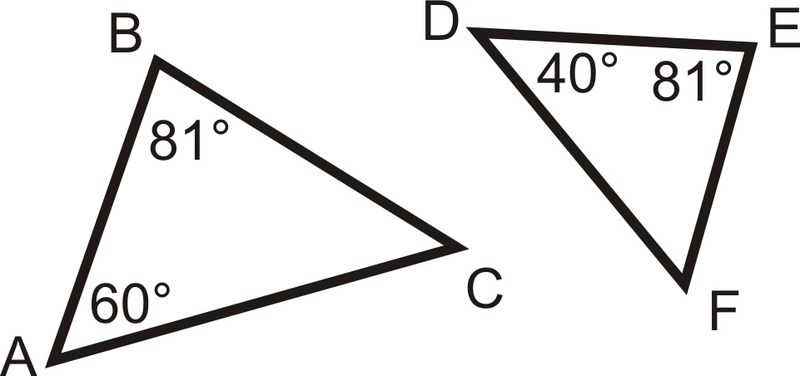
Solución

Compara los ángulos para ver si podemos usar el Postulado de Similitud AA. Usando el teorema de la suma del triángulo,$m\angle C=39^{\circ}$ y$m\angle F=59^{\circ}$. $m\angle C\neq m\angle F$, Entonces$\Delta ABC$ y no$\Delta DEF$ son similares.

Ejemplo$\PageIndex{5}$

$\Delta LEG\sim \Delta MAR$por AA. Encontrar$GE$ y$MR$.

Figura$\PageIndex{6}$

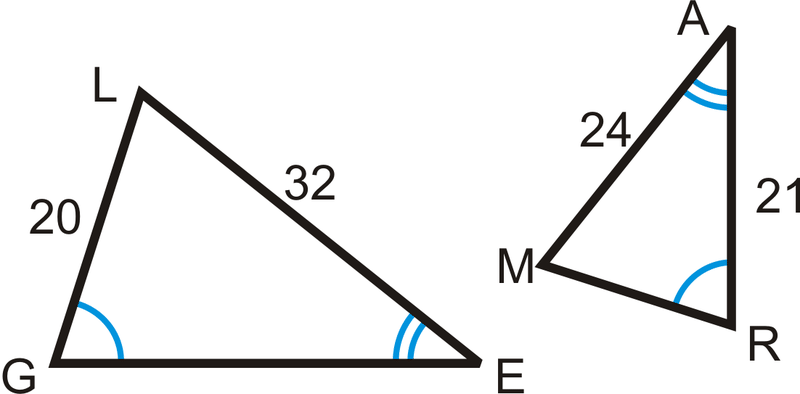
Solución

Establezca una proporción para encontrar los lados faltantes.

\ (\ begin {array} {rlrl}
\ frac {24} {32} & =\ frac {M R} {20} &\ frac {24} {32} & =\ frac {21} {G E}\
480 & =32 M R & 24 G E & =672\
15 & =M R & G E&=28
\ end {array}\)

Cuando dos triángulos son similares, los lados correspondientes son proporcionales. Pero, ¿cuáles son los lados correspondientes? Usando los triángulos de este ejemplo, vemos cómo los lados se alinean en el diagrama a la derecha.

Figura$\PageIndex{7}$

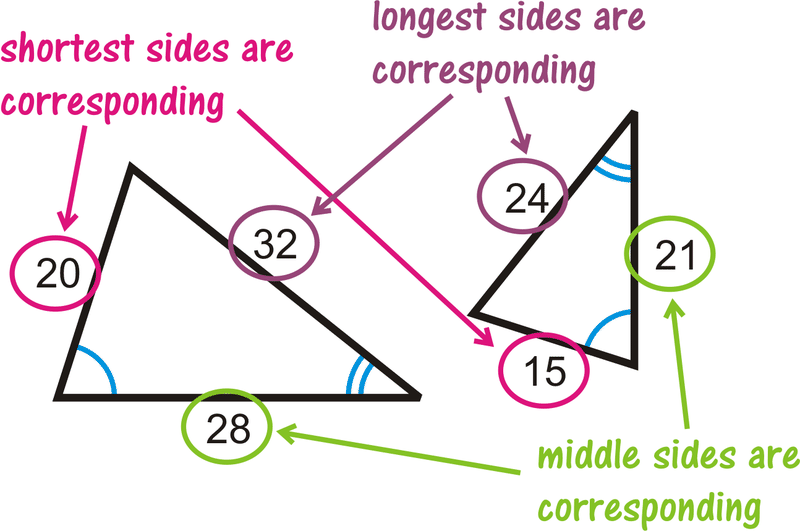
Revisar

Utilice el diagrama para completar cada sentencia.

Figura$\PageIndex{8}$

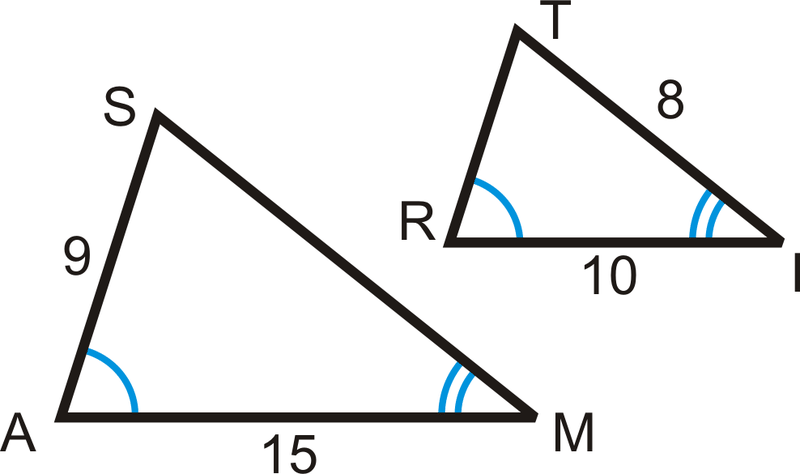
1. $\Delta SAM\sim \Delta ______$
2. $\dfrac{SA}{?}=\dfrac{SM}{?}=\dfrac{?}{RI}$
3. $SM = ______$
4. $TR = ______$
5. $\dfrac{9}{?}=\dfrac{?}{8}$

Responder preguntas 6-9 sobre trapecio$ABCD$.

Figura$\PageIndex{9}$

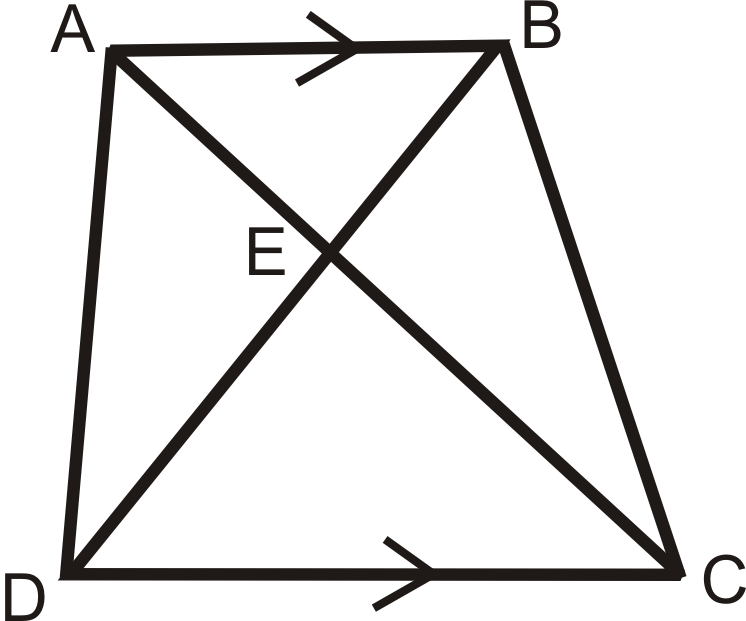
6. Nombra dos triángulos similares. ¿Cómo sabes que son similares?
7. Escribe una verdadera proporción.
8. Nombra otros dos triángulos que podrían no ser similares.
9. Si$AB=10$,$AE=7$, y$DC=22$, encuentra$AC$. ¡Ten cuidado!

Usa los triángulos de la izquierda para las preguntas 10-14.

$AB=20$,$DE=15$, y$BC=k$.

Figura$\PageIndex{10}$

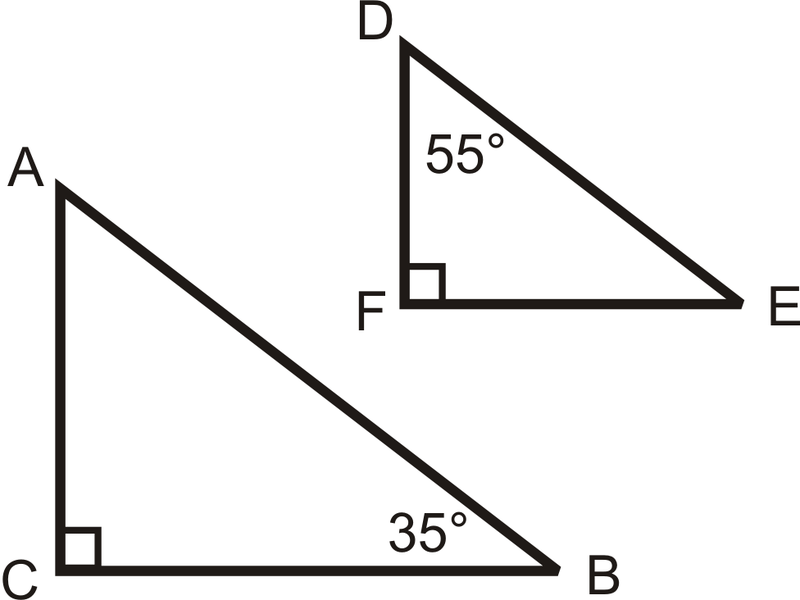
10. ¿Los dos triángulos son similares? ¿Cómo lo sabes?
11. Escribir una expresión para$FE$ en términos de$k$.
12. Si$FE=12$, ¿qué es$k$?
13. Rellene los espacios en blanco: Si un ángulo agudo de un triángulo _______ es congruente con un ángulo agudo en otro triángulo ________, entonces los dos triángulos son _______.
14. Redacción ¿En qué se diferencian los triángulos congruentes y los triángulos similares? ¿Cómo son iguales?

¿Son similares los siguientes triángulos? Si es así, escriba una declaración de similitud.

15. 

    Figura$\PageIndex{11}$

16. 

    Figura$\PageIndex{12}$

17. 

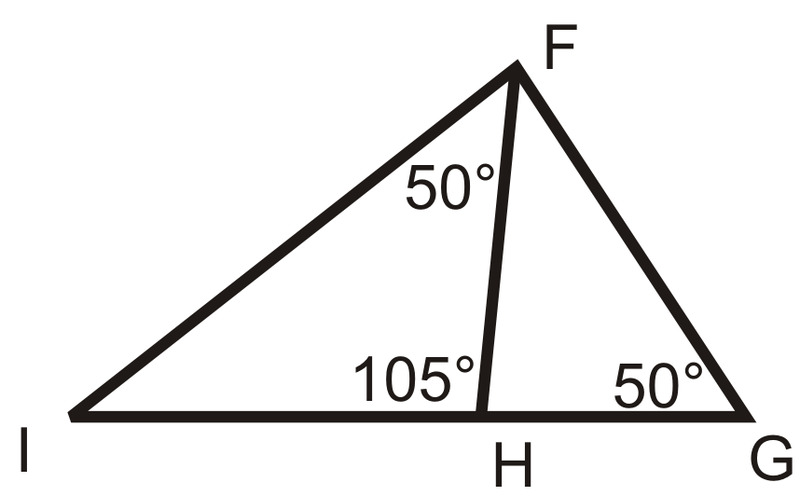
    Figura$\PageIndex{13}$

18. 

    Figura$\PageIndex{14}$

19. 

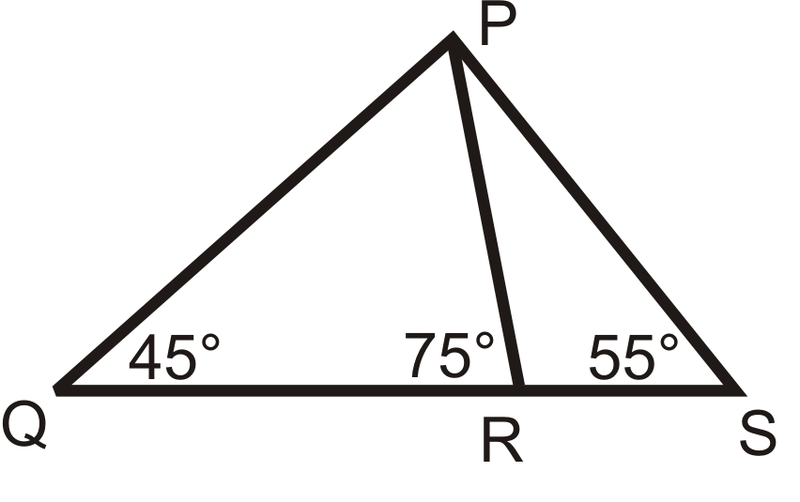
    Figura$\PageIndex{15}$

20. 

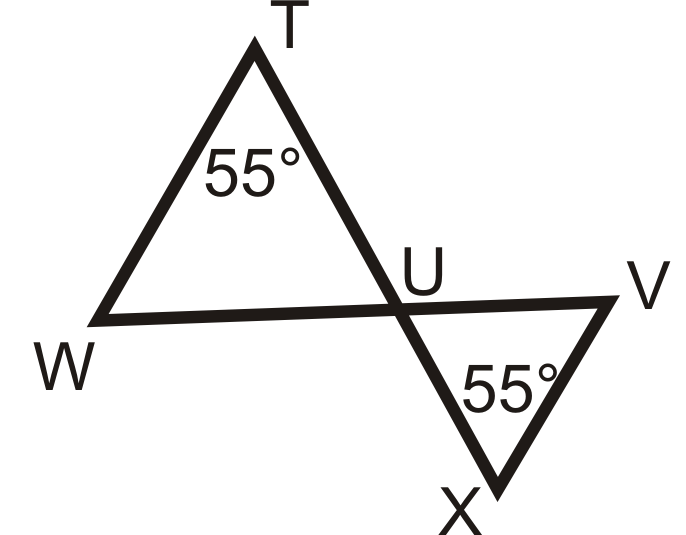
    Figura$\PageIndex{16}$

21. 

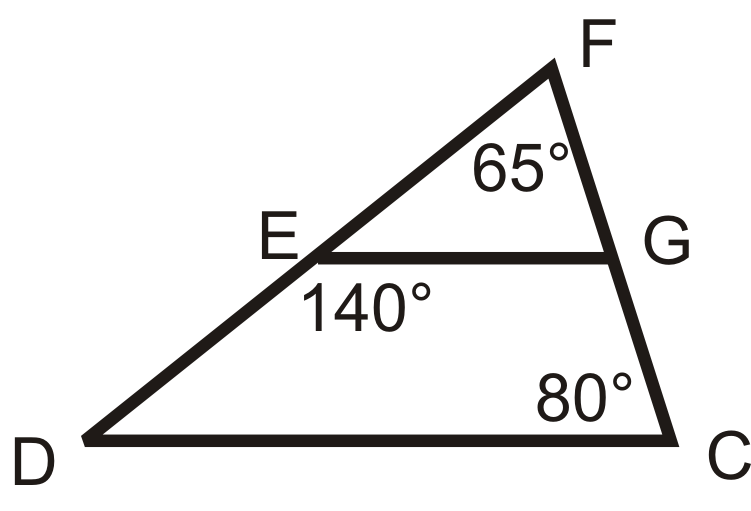
    Figura$\PageIndex{17}$

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.4.

Recursos

El vocabulario

Término	Definición
triángulos similares	Dos triángulos donde todos sus ángulos correspondientes son congruentes (exactamente iguales) y sus lados correspondientes son proporcionales (en la misma proporción).
Postulado de similitud AA	Si dos ángulos en un triángulo son congruentes con dos ángulos en otro triángulo, entonces los dos triángulos son similares.
Dilatación	Reducir o agrandar una figura según un factor de escala es una dilatación.
Teorema de suma de triángulo	El Teorema de la Suma del Triángulo establece que los tres ángulos interiores de cualquier triángulo suman 180 grados.
Transformación Rígida	Una transformación rígida es una transformación que conserva la distancia y los ángulos, no cambia el tamaño ni la forma de la figura.

Recursos adicionales

Elemento Interactivo

Video: Triángulos Congruentes y Similares

Actividades: AA Similaridad Preguntas de Discusión

Ayudas de estudio: Guía de estudio de similitud poligonal

Práctica: Similaridad AA

Mundo real: Crazy Quilt