7.14: Teoremas que involucran similitud
( \newcommand{\kernel}{\mathrm{null}\,}\)
Demostrar y utilizar los teoremas de Proporcionalidad Triangular, Bisectriz de Ángulo Triángulo y Pitágoras.
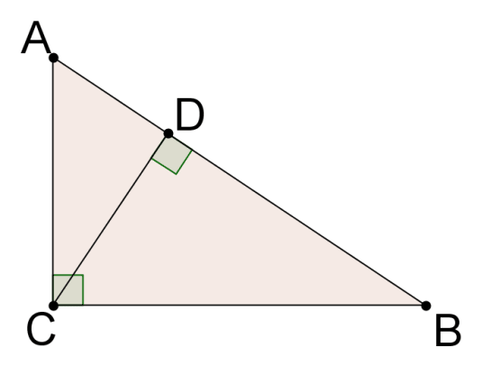
¿Puedes encontrar algún triángulo similar en la imagen de abajo?
Teoremas sobre Triángulos Similares
Si dos triángulos son similares, entonces sus ángulos correspondientes son congruentes y sus lados correspondientes son proporcionales. Hay muchos teoremas sobre triángulos que puedes probar usando triángulos similares.
- Teorema de la proporcionalidad del triángulo: Una línea paralela a un lado de un triángulo divide proporcionalmente los otros dos lados del triángulo. Este teorema y su inverso serán explorados y probados en #1 y #2, y los ejercicios de Revisión.
- Teorema de la bisectriz del ángulo del triángulo: El ángulo bisectriz de un ángulo de un triángulo divide el lado opuesto del triángulo en segmentos proporcionales a las longitudes de los otros dos lados del triángulo. Este teorema será explorado y probado en #3.
- Teorema de Pitágoras: Para un triángulo rectángulo con patas a y b e hipotenusa c,a^2+b^2=c^2. Este teorema será explorado y probado en los problemas de Ejemplos.
Echemos un vistazo a algunos problemas sobre probar la similitud de triángulos.
1. \Delta ADE\sim \Delta ABCDemuéstralo.
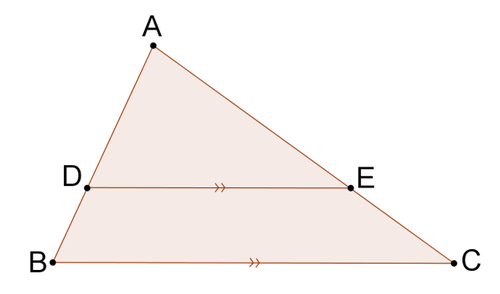
Los dos triángulos comparten\angle A. Porque\overline{DE}\parallel \overline{BC}, los ángulos correspondientes son congruentes. Por lo tanto,\angle ADE\cong \angle ABC. Los dos triángulos tienen dos pares de ángulos congruentes. Por lo tanto,\Delta ADE\sim \Delta ABC por AA\ sim\).
2. Usa tu resultado de #1 para demostrarlo\dfrac{AB}{AD}=\dfrac{AC}{AE}. Entonces, usa álgebra para demostrarlo\dfrac{DB}{AD}=\dfrac{EC}{AE}.
\(\Delta ADE\sim \Delta ABC\)lo que significa que los lados correspondientes son proporcionales. Por lo tanto,\dfrac{AB}{AD}=\dfrac{AC}{AE}. Ahora, puedes usar álgebra para demostrar que la segunda proporción debe ser cierta. Recuerda esoAB=AD+DB yAC=AE+EC.
\begin{aligned}\dfrac{AB}{AD}&=\dfrac{AC}{AE} \\ \rightarrow \dfrac{AD+DB}{AD}&=AE+\dfrac{EC}{AE} \\ \rightarrow 1+\dfrac{DB}{AD}&=1+\dfrac{EC}{AE} \\ \rightarrow \dfrac{DB}{AD}&=\dfrac{EC}{AE}\end{aligned}
Ahora has probado el teorema de la proporcionalidad del triángulo: una línea paralela a un lado de un triángulo divide proporcionalmente los otros dos lados del triángulo.
3. Considerar\Delta ABC con\overline{AE} el ángulo bisectriz de\angle BAC y puntoD construido de manera que\overline{DC}\parallel \overline{AE}. \dfrac{EB}{BA}=\dfrac{EC}{CA}Demuéstralo.
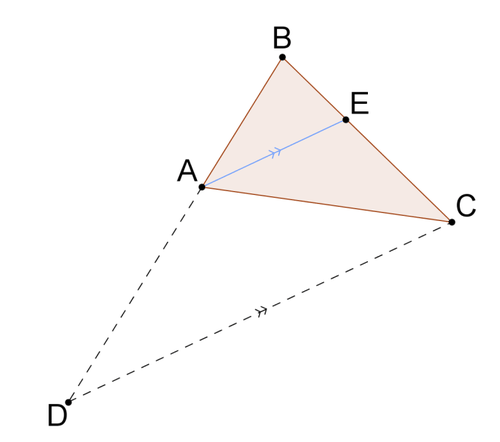
Por el teorema de la proporcionalidad del triángulo,\dfrac{EB}{EC}=\dfrac{BA}{AD}. Multiplique ambos lados de esta proporción por\dfrac{EC}{BA}.
\begin{aligned}(\dfrac{EC}{BA})\cdot \dfrac{EB}{EC} \\ \rightarrow \dfrac{EB}{BA}=\dfrac{BA}{AD}\cdot (\dfrac{EC}{BA})=\dfrac{EC}{AD}\end{aligned}
Ahora todo lo que necesitas mostrar es esoAD=CA para poder probar el resultado deseado.
- Porque\overline{AE} es el ángulo bisectriz de\angle BAC,\angle BAE\cong \angle EAC.
- Porque\overline{DC}\parallel \overline{AE},\angle BAE\cong \angle BDC (ángulos correspondientes).
- Porque\overline{DC}\parallel \overline{AE},\angle EAC\cong \angle DCA (alternar ángulos interiores).
- Así,\angle BDC\cong \angle DCA por la propiedad transitiva.
Por lo tanto,\Delta ADC es isósceles porque sus ángulos de base son congruentes y debe ser cierto que\overline{AD}\cong \overline{CA}. Esto significa queAD=CA. Por lo tanto:
\dfrac{EB}{BA}=\dfrac{EC}{CA}
Esto prueba el teorema de la bisectriz del ángulo del triángulo: el ángulo bisectriz de un ángulo de un triángulo divide el lado opuesto del triángulo en segmentos proporcionales a las longitudes de los otros dos lados del triángulo.
Ejemplo\PageIndex{1}
Anteriormente, te preguntaron ¿puedes encontrar algún triángulo similar en la imagen de abajo?

Solución
Hay tres triángulos en esta imagen:\Delta BAC,\Delta BCD,\Delta CAD. Los tres triángulos son triángulos rectos por lo que tienen un conjunto de ángulos congruentes (el ángulo recto). \Delta BACy\Delta BCD compartir\angle B, entonces\Delta BAC\sim \Delta BCD by \(AA\sim. De igual manera,\Delta BAC y\Delta CAD compartir\angle C, así\Delta BAC\sim \Delta CAD porAA\sim. Por la propiedad transitiva, los tres triángulos deben ser similares entre sí.
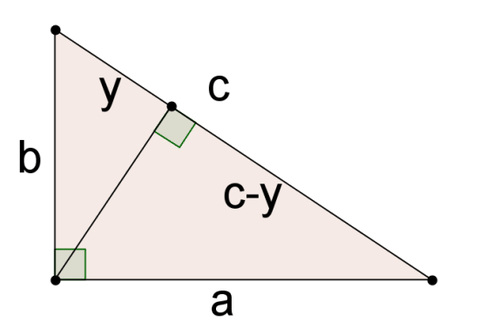
El triángulo grande de arriba tiene ladosa,b, yc. Lateral sec ha dividido en dos partes:y yc−y. En el Concepto Problema Revisitado mostraste que los tres triángulos en esta imagen son similares.
Ejemplo\PageIndex{2}
Explique por qué\dfrac{a}{c}=\dfrac{c-y}{a}.
Solución
Cuando los triángulos son similares, los lados correspondientes son proporcionales. Coincidir cuidadosamente con los lados correspondientes y ya lo ves\dfrac{a}{c}=\dfrac{c-y}{a}.
Ejemplo\PageIndex{3}
Explique por qué\dfrac{b}{c}=\dfrac{y}{b}.
Solución
Cuando los triángulos son similares, los lados correspondientes son proporcionales. Coincidir cuidadosamente con los lados correspondientes y ya lo ves\dfrac{b}{c}=\dfrac{y}{b}.
Ejemplo\PageIndex{4}
Usa los resultados de #2 y #3 para demostrarloa^2+b^2=c^2.
Solución
Multiplicar cruzado para reescribir cada ecuación. Después, sumar las dos ecuaciones juntas.
\begin{aligned} \dfrac{a}{c}&=\dfrac{c-y}{a}\rightarrow a^2=c^2−cy \\ \dfrac{b}{c}&=\dfrac{y}{b}\rightarrow b^2=cy \\ \rightarrow a^2+b^2&=c^2−cy+cy \\ \rightarrow a^2+b^2&=c^2 \end{aligned}
Acabas de probar el Teorema de Pitágoras usando triángulos similares.
Revisar
Resolver parax en cada problema.
-
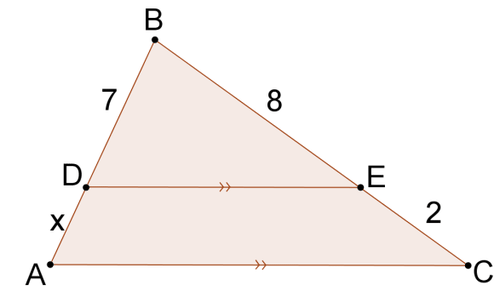
Figura\PageIndex{6} -
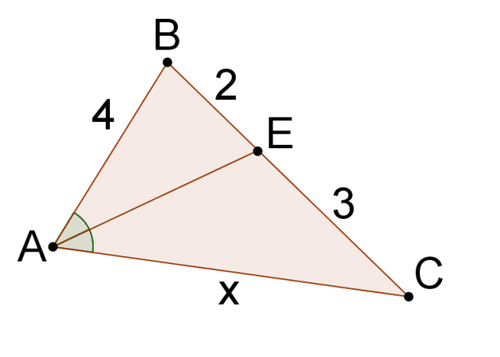
Figura\PageIndex{7} -
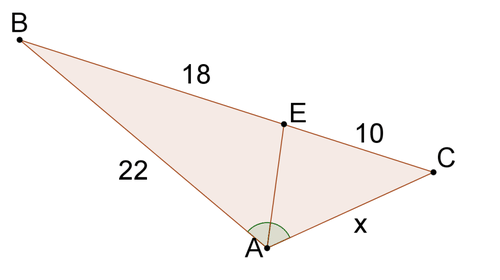
Figura\PageIndex{8} -
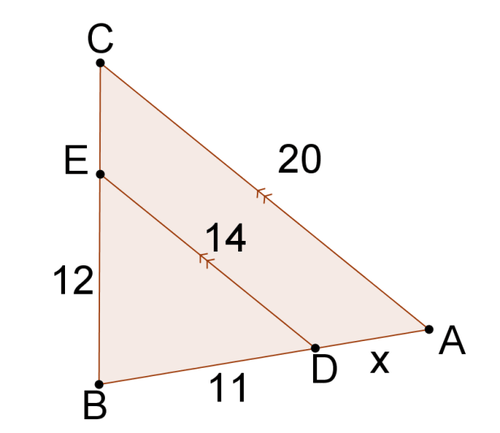
Figura\PageIndex{9} -

Figura\PageIndex{10} -

Figura\PageIndex{11} -
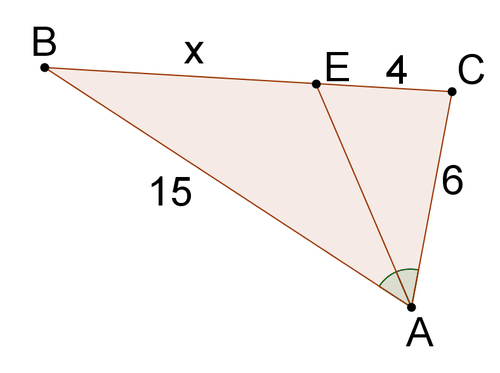
Figura\PageIndex{12}
Usa la imagen de abajo para #8 - #10.
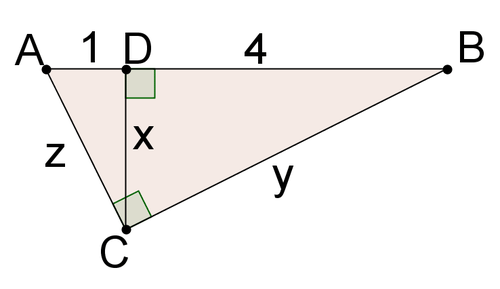
8. Resolver parax.
9. Resolver paraz.
10. Resolver paray.
Usa la imagen de abajo para #11 - #13.
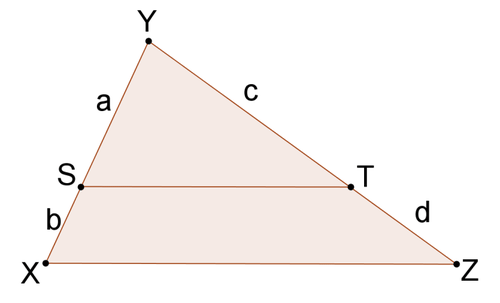
11. Asumir eso\dfrac{b}{a}=\dfrac{d}{c}. Usa álgebra para demostrarlo\dfrac{b+a}{a}=\dfrac{d+c}{c}.
12. Demostrar que\Delta YST\sim \Delta YXZ
13. Demostrar que\overline{ST}\parallel \overline{XZ}
14. Demostrar que un segmento que conecta los puntos medios de dos lados de un triángulo será paralelo al tercer lado del triángulo.
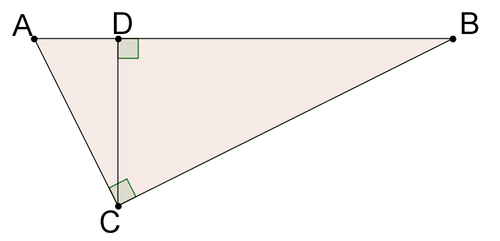
15. Demostrar el Teorema de Pitágoras usando la imagen de abajo.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.6.
El vocabulario
| Término | Definición |
|---|---|
| Teorema de Pitágoras | El Teorema de Pitágoras es una relación matemática entre los lados de un triángulo rectánguloa^2+b^2=c^2, dada por, dondea yb son patas del triángulo yc es la hipotenusa del triángulo. |
| Teorema de la proporcionalidad del triángulo | El Teorema de Proporcionalidad Triangular establece que si una línea es paralela a un lado de un triángulo e intersecta los otros dos lados, entonces divide esos lados proporcionalmente. |
| Teorema de Bisectriz de Ángulo | El ángulo bisectriz de un ángulo de un triángulo divide el lado opuesto del triángulo en segmentos proporcionales a las longitudes de los otros dos lados del triángulo. |


