7.15: Dilatación de una Forma
- Page ID
- 107454
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Versión mayor o menor de una figura que conserva su forma.
Dilatación
Dos figuras son similares si son de la misma forma pero no necesariamente del mismo tamaño. Una forma de crear figuras similares es dilatando. Una dilatación hace que una figura sea más grande o menor pero la nueva figura resultante tiene la misma forma que la original.
Dilatación: Un agrandamiento o reducción de una figura que conserva la forma pero no el tamaño. Todas las dilataciones son similares a la figura original.
Las dilataciones tienen un centro y un factor de escala. El centro es el punto de referencia para la dilatación y el factor de escala nos dice cuánto se estira o encoge la figura. Se etiqueta un factor de escala\(k\). Sólo los factores de escala positivos\(k\),, serán considerados en este texto.
Si la imagen dilatada es menor que la original, entonces\(0<k<1\).
Si la imagen dilatada es mayor que la original, entonces\(k>1\).
Una dilatación, o imagen, siempre va seguida de un\(′\).
| Etiquetarlo | Dilo |
|---|---|
| \(′\) | “prime” (copia del original) |
| \(A′\) | “a prime” (copia de punto\(A\)) |
| \(A′′\) | “a double prime” (segunda copia) |
¿Y si agrandaste o redujiste un triángulo sin cambiar su forma? ¿Cómo se pudo encontrar el factor de escala por el cual se estiró o encogió el triángulo?
Ejemplo\(\PageIndex{1}\)
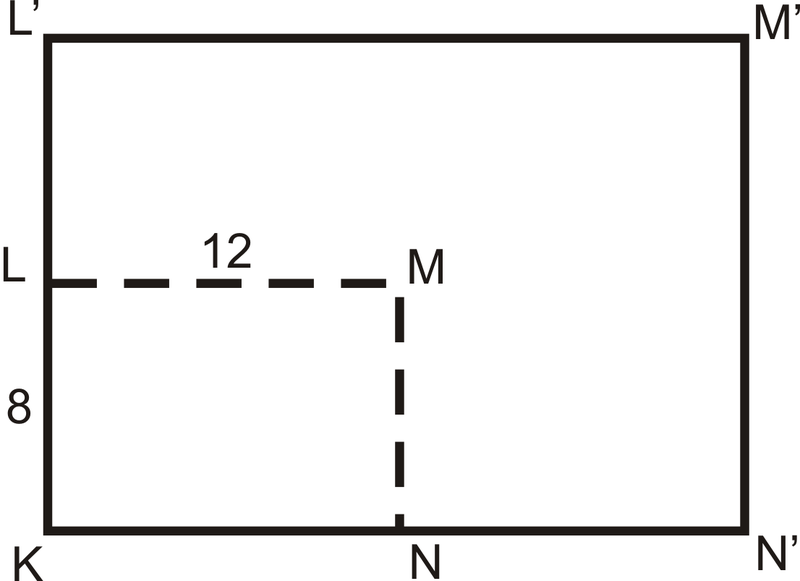
Encuentra los perímetros de\(KLMN\) y\(K′L′M′N′\). Compara esta relación con el factor de escala.
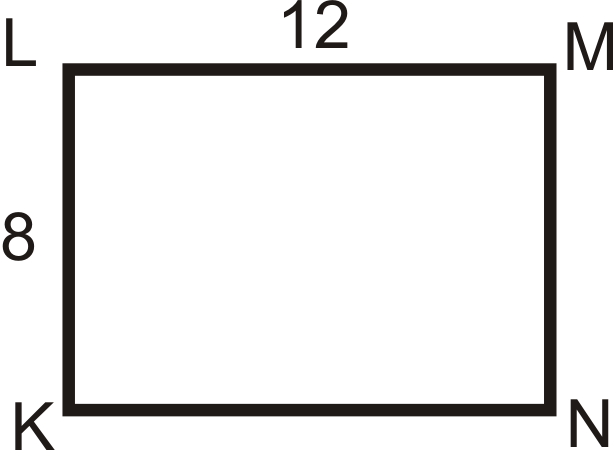
Solución
El perímetro de\(KLMN=12+8+12+8=40\). El perímetro de\(K′L′M′N′=24+16+24+16=80\). La relación es de 80:40, que se reduce a 2:1, que es lo mismo que el factor de escala.
Ejemplo\(\PageIndex{2}\)
\(\Delta ABC\)es una dilatación de\(\Delta DEF\). Si P es el centro de dilatación, ¿cuál es el factor de escala?
Solución
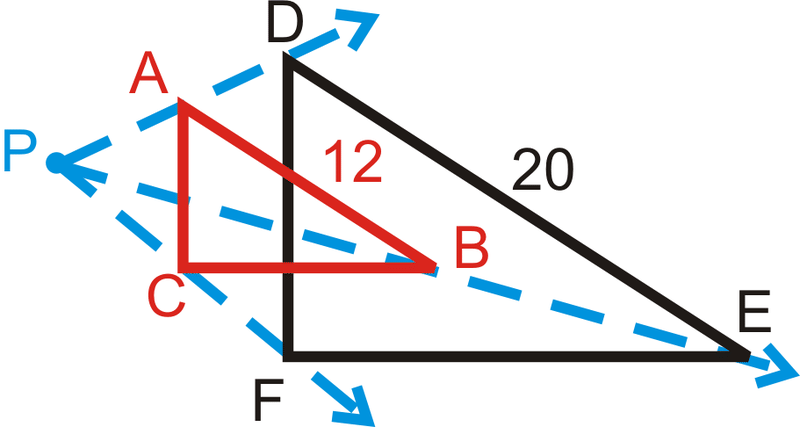
Porque\(\Delta ABC\) es una dilatación de\(\Delta DEF\), entonces\(\Delta ABC\sim \Delta DEF\). El factor de escala es la relación de los lados. Dado que\(\Delta ABC\) es menor que el original\(\Delta DEF\),, el factor de escala va a ser menor que uno,\(\dfrac{12}{20}=\dfrac{3}{5}\).
Si\(\Delta DEF\) fuera la imagen dilatada, el factor de escala habría sido\(\dfrac{5}{3}\).
Ejemplo\(\PageIndex{3}\)
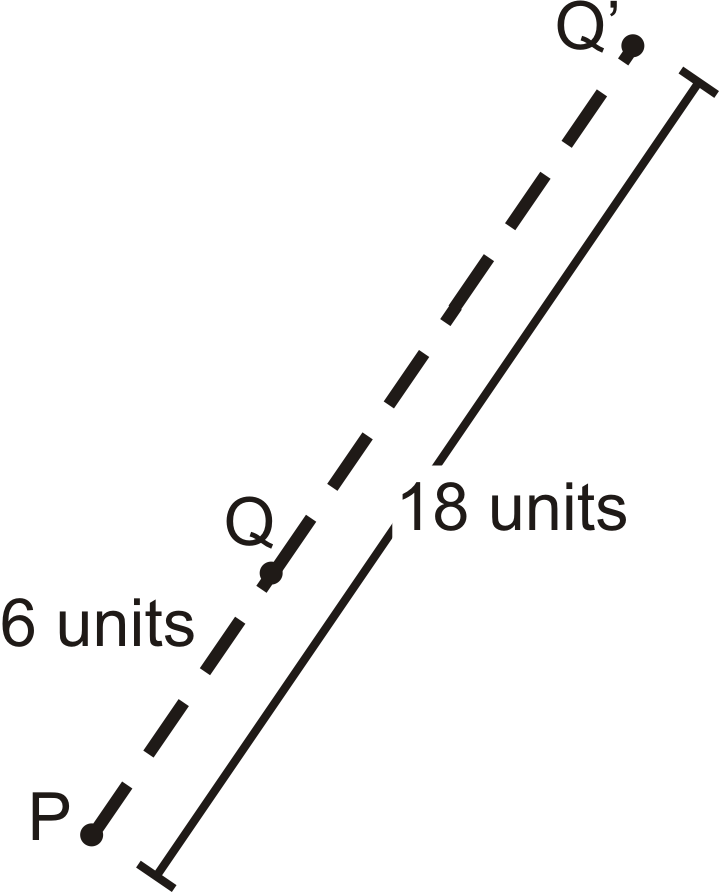
El centro de dilatación es\(P\) y el factor de escala es 3.
Encuentra\(Q′\).
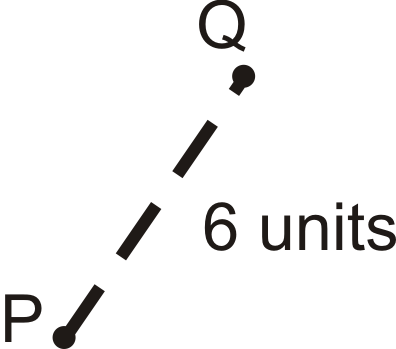
Solución
Si el factor de escala es 3 y\(Q\) está a 6 unidades de distancia\(P\), entonces\(Q′\) va a ser\(6\times 3=18\) unidades de distancia de\(P\). La imagen dilatada estará en la misma línea que la imagen original y el centro.
Ejemplo\(\PageIndex{4}\)
Usando la imagen de arriba, cambie el factor de escala a 13.
Encuentra\(Q′′\) usando este nuevo factor de escala.
Solución
El factor de escala es\(\dfrac{1}{3}\), por lo que\(Q′′\) va a ser\(6\times \dfrac{1}{3}=2\) unidades de distancia de\(P\). \(Q′′\)también será colineal con\(Q\) y centro.
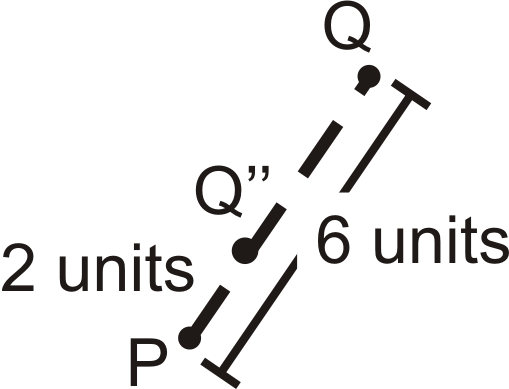
Ejemplo\(\PageIndex{5}\)
\(KLMN\)es un rectángulo. Si el centro de dilatación es\(K\) y\(k=2\), dibuja\(K′L′M′N′\).
Solución
Si\(K\) es el centro de dilatación, entonces\(K\) y\(K′\) será el mismo punto. A partir de ahí,\(L′\) serán 8 unidades arriba\(L\) y\(N′\) serán 12 unidades a la derecha de\(N\).
Revisar
Para las formas dadas, dibuje la dilatación, dado el factor de escala y el centro.
- \(k=3.5\), el centro es\(A\)
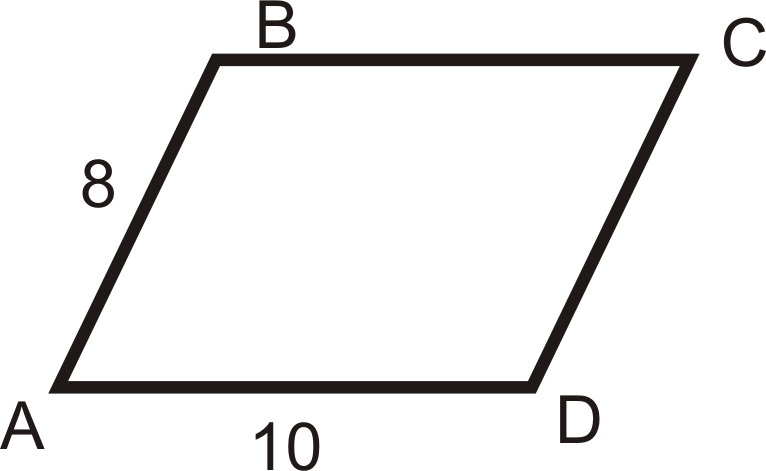
- \(k=2\), el centro es\(D\)
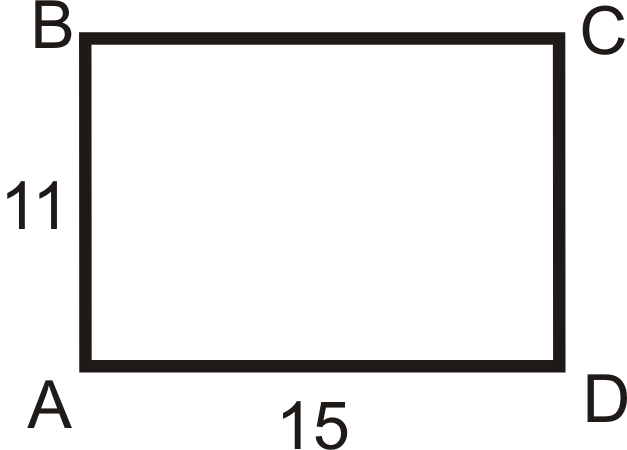
- \(k=\dfrac{3}{4}\), el centro es\(A\)
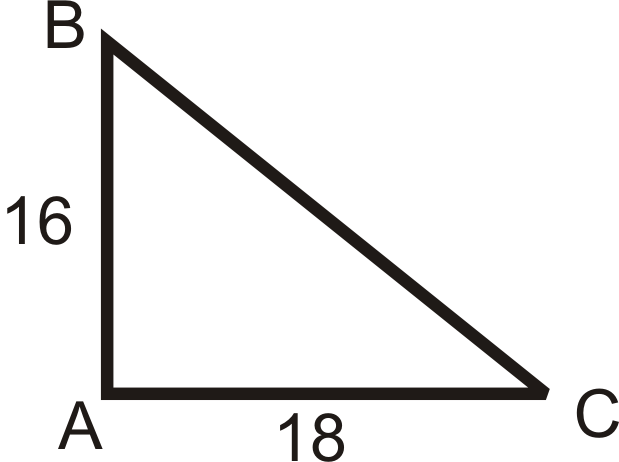
- \(k=\dfrac{2}{5}\), el centro es A\)
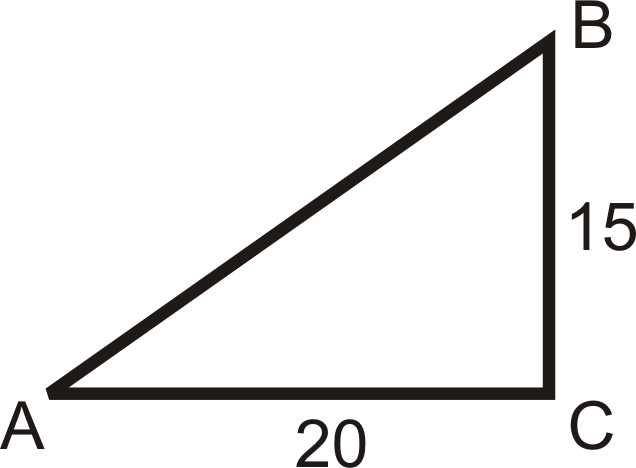
En las cuatro preguntas que aparecen a continuación, se le indica el factor de escala. Determinar las dimensiones de la dilatación. En cada diagrama, la figura negra es la original y\(P\) es el centro de dilatación.
- \(k=4\)
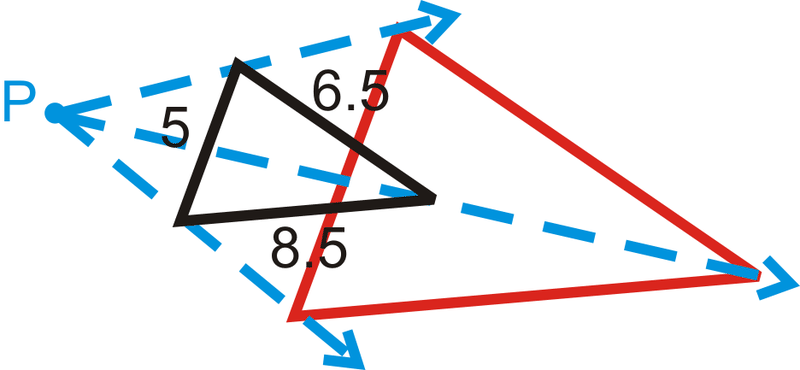
- \(k=\dfrac{1}{3}\)
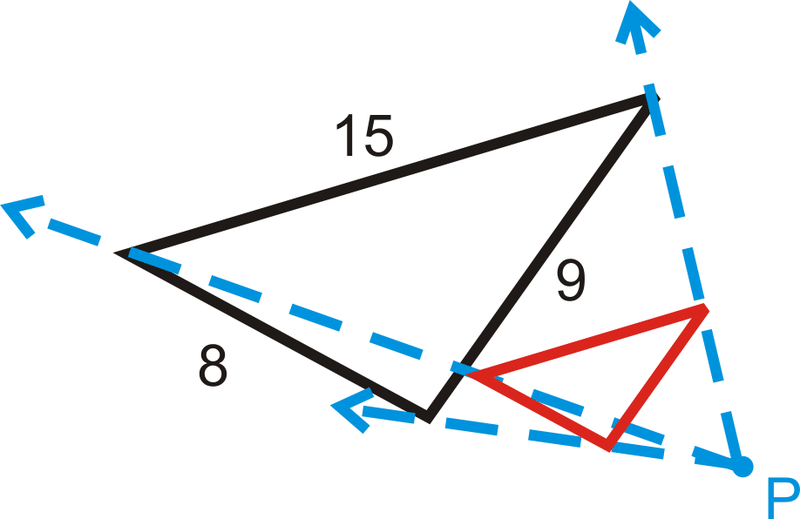
- \(k=2.5\)
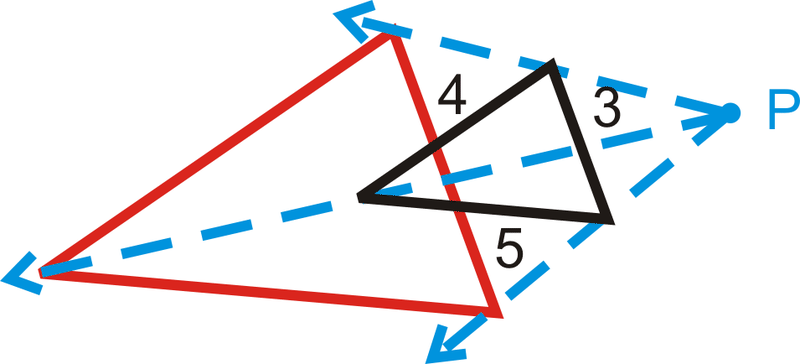
- \(k=\dfrac{1}{4}\)
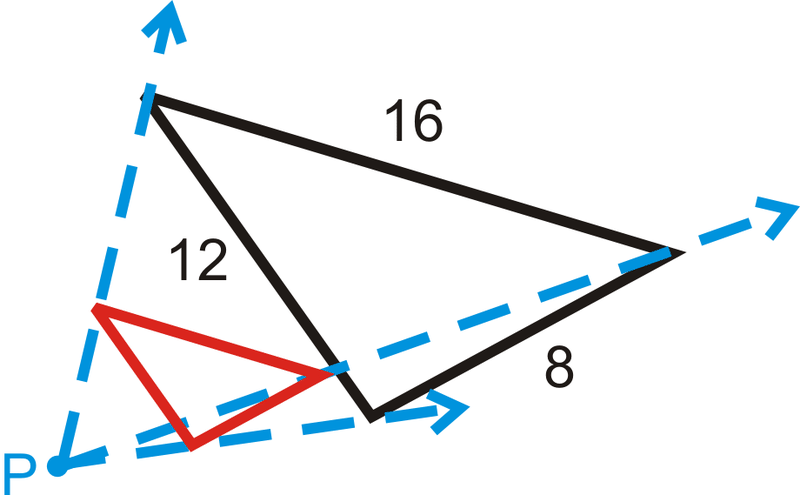
En las tres preguntas siguientes, encuentra el factor de escala, dadas las caras correspondientes. En cada diagrama, la figura negra es la original y\(P\) es el centro de dilatación.
-
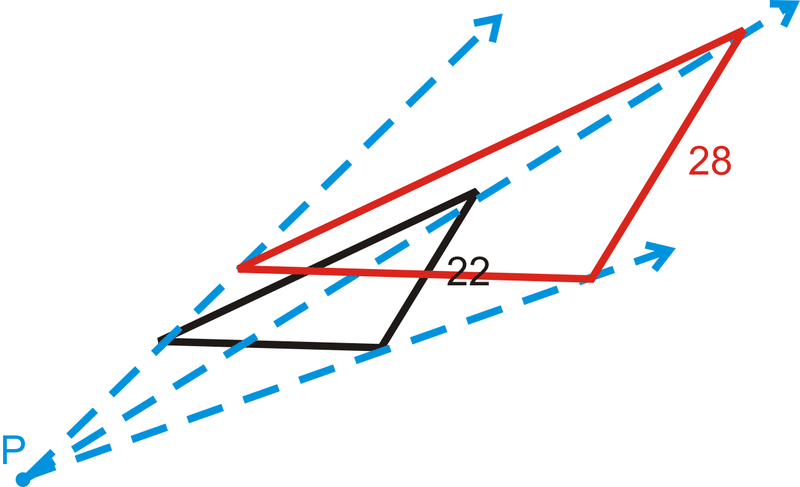
Figura\(\PageIndex{17}\) -
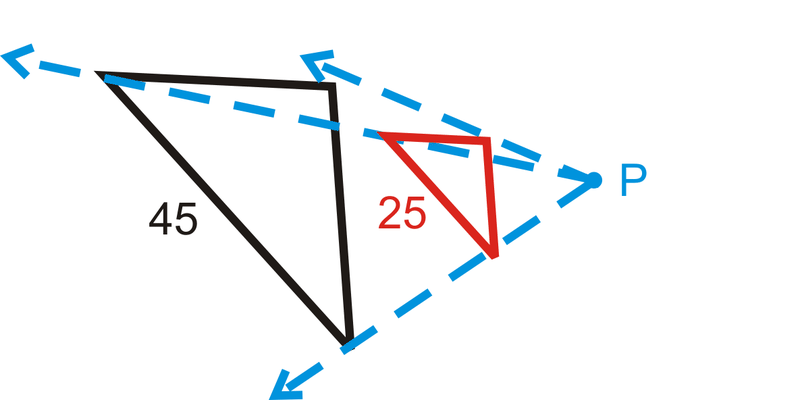
Figura\(\PageIndex{18}\) -
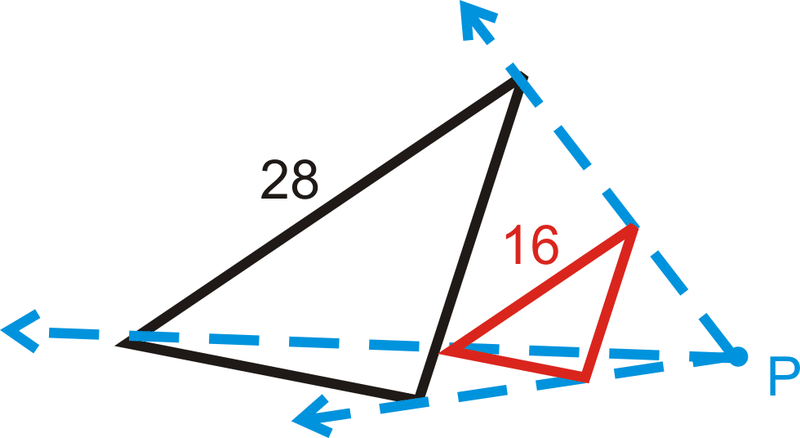
Figura\(\PageIndex{19}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.11.
vocabulario
| Término | Definición |
|---|---|
| Dilatación | Reducir o agrandar una figura según un factor de escala es una dilatación. |
| Cuadrilátero | Un cuadrilátero es una figura cerrada con cuatro lados y cuatro vértices. |
| Ratio | Una relación es una comparación de dos cantidades que se pueden escribir en forma de fracción, con dos puntos o con la palabra “a”. |
| Factor de Escala | Un factor de escala es una relación entre la escala y la dimensión original o real escrita en la forma más simple. |
| Transformación | Una transformación mueve una figura de alguna manera en el plano de coordenadas. |
| Vertex | Un vértice es un punto de intersección de las líneas o rayos que forman un ángulo. |
| Transformación Rígida | Una transformación rígida es una transformación que conserva la distancia y los ángulos, no cambia el tamaño ni la forma de la figura. |
Recursos adicionales
Elemento Interactivo
Video: Principios de dilatación - Básico
Actividades: Preguntas de discusión sobre dilatación
Ayudas de estudio: Guía de estudio de tipos de transformaciones
Práctica: Dilatación de una Forma
Mundo real: El efecto CSI