7.16: Dilatación en el Plano Coordenado

Multiplicación de coordenadas por un factor de escala dado el origen como centro.

Dilatación en el plano de coordenadas

Dos figuras son similares si son de la misma forma pero no necesariamente del mismo tamaño. Una forma de crear figuras similares es dilatando. Una dilatación hace que una figura sea más grande o menor de tal manera que la nueva imagen tenga la misma forma que la original.

Dilatación: Un agrandamiento o reducción de una figura que conserva la forma pero no el tamaño. Todas las dilataciones son similares a la figura original.

Las dilataciones tienen un centro y un factor de escala. El centro es el punto de referencia para la dilatación y el factor de escala nos dice cuánto se estira o encoge la figura. Se etiqueta un factor de escala\(k\). Sólo los factores de escala positivos\(k\),, serán considerados en este texto.

Si la imagen dilatada es menor que la original, entonces\(0<k<1\).

Si la imagen dilatada es mayor que la original, entonces\(k>1\).

Para dilatar algo en el plano de coordenadas, multiplica cada coordenada por el factor de escala. A esto se le llama mapeo . Para cualquier dilatación el mapeo será\((x,y)\rightarrow (kx,ky)\). En este texto, el centro de dilatación siempre será el origen.

¿Y si se le dieran las coordenadas de una figura y se le pidiera que dilatara esa figura en un factor de escala de 2? ¿Cómo pudiste encontrar las coordenadas de la figura dilatada?

Para los Ejemplos 1 y 2, use las siguientes instrucciones:

Dado A y el factor de escala, determinar las coordenadas del punto dilatado,\(A′\). Se puede suponer que el centro de dilatación es el origen. Recuerda que el mapeo será\((x, y)\rightarrow (kx, ky)\).

Ejemplo\(\PageIndex{1}\)

\(A(−4,6), k=2\)

Solución

\(A′(−8,12)\)

Ejemplo\(\PageIndex{2}\)

\(A(9,−13), k=\dfrac{1}{2}\)

Solución

\(A′(4.5,−6.5)\)

Ejemplo\(\PageIndex{3}\)

El cuadrilátero EFGH\) tiene vértices\(E(−4,−2)\),\(F(1,4)\),\(G(6,2)\) y\(H(0,−4)\). Dibuja la dilatación con un factor de escala de 1.5.

Figura\(\PageIndex{1}\)

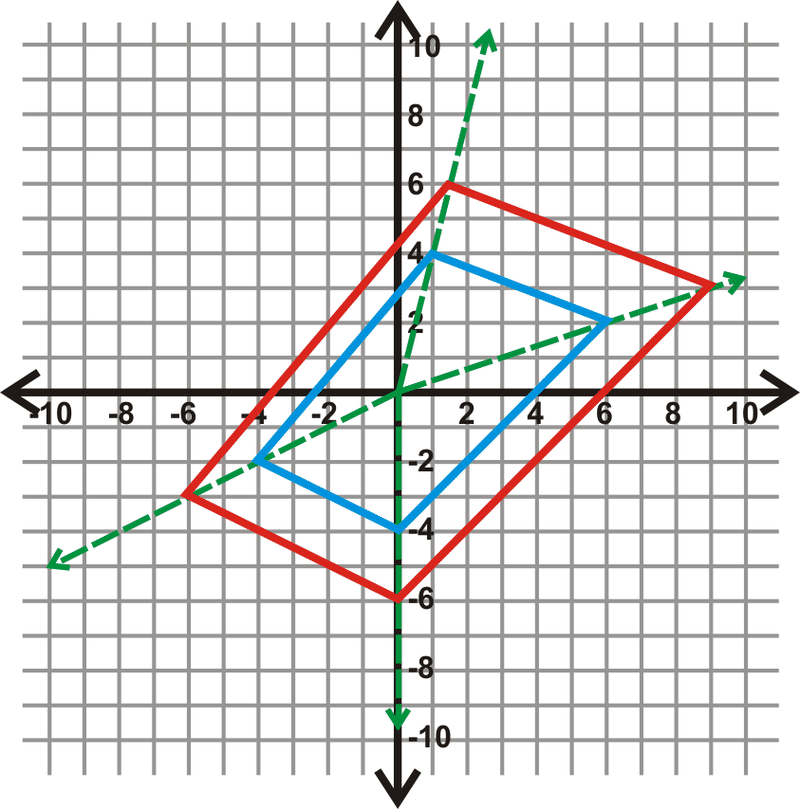
Solución

Recuerda que para dilatar algo en el plano de coordenadas, multiplica cada coordenada por el factor de escala.

Para esta dilatación, el mapeo será\ ((x, y)\ fila derecha (1.5x, 1.5y).

\(\begin{aligned} &E(−4,−2)\rightarrow (1.5(−4),1.5(−2))\rightarrow E′(−6,−3) \\ &F(1,4)\rightarrow (1.5(1),1.5(4))\rightarrow F′(1.5,6) \\ &G(6,2)\rightarrow (1.5(6),1.5(2))\rightarrow G′(9,3) \\ &H(0,−4)\rightarrow (1.5(0),1.5(−4))\rightarrow H′(0,−6)\end{aligned}\)

En la gráfica anterior, el cuadrilátero azul es el original y la imagen roja es la dilatación.

Ejemplo\(\PageIndex{4}\)

Determinar las coordenadas\(\Delta ABC\)\(\Delta A′B′C′\) y encontrar el factor de escala.

Figura\(\PageIndex{2}\)

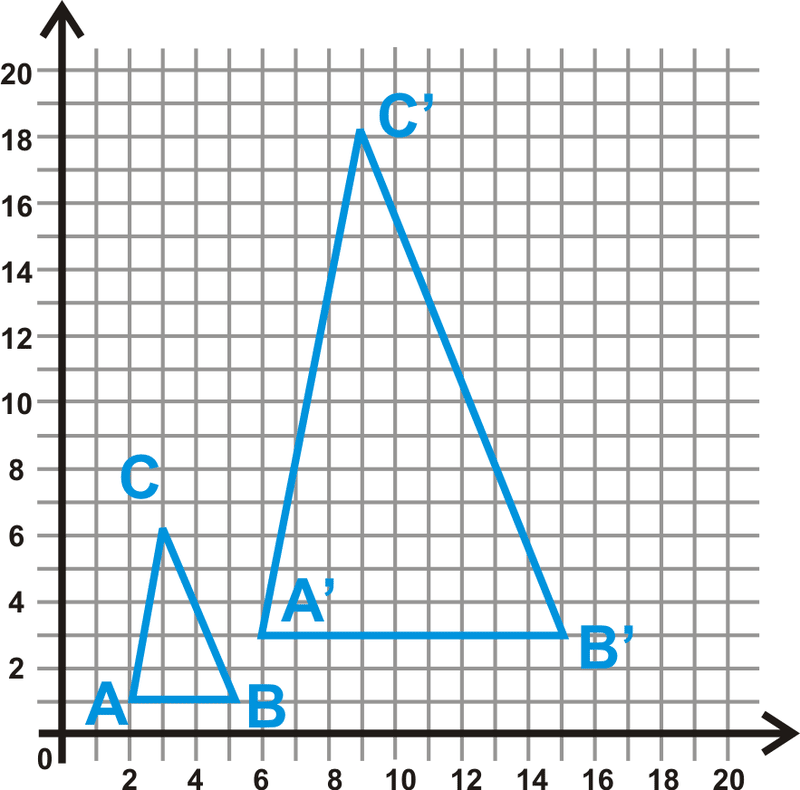
Solución

Las coordenadas de los vértices de\(\Delta ABC\) son\(A(2,1)\), B (5,1)\) y C (3,6)\). Las coordenadas de los vértices de\(\Delta A′B′C′\) son A′ (6,3)\)\(B′(15,3)\) y C′ (9,18)\). Cada una de las coordenadas correspondientes son tres veces las originales, entonces\(k=3\).

Ejemplo\(\PageIndex{5}\)

Demuestre que las dilataciones preservan la forma usando la fórmula de distancia. Encuentra las longitudes de los lados de ambos triángulos en el Ejemplo B.

Solución

\ (\ begin {array} {ll}\ subrayado {\ Delta ABC} &\ subrayado {\ Delta A'B'C'}
A B=\ sqrt {(2-5) ^ {2} + (1-1) ^ {2}} =\ sqrt {9} =3 y A^ {\ prime} B^ {\ prime} =\ sqrt {(6-15) ^ {2} + (3-3) ^ {2}} =\ sqrt {81} =9\\
A C=\ sqrt {(2-3) ^ {2} + (1-6) ^ {2}} =\ sqrt {26} y A^ {\ prime} C^ {\ prime} =\ sqrt {(6-9) ^ {2} + (3-18) ^ {2}} =3\ sqrt {26}\
C B=\ sqrt {(3-5) ^ {2} + (6-1) ^ {2}} =\ sqrt {29} & C^ {\ prime} B^ {\ prime} =\ sqrt {(9-15) ^ {2} + (18-3) ^ {2}} =3\ sqrt {29}
\ end {array}\)

A partir de esto, también vemos que todos los lados de\(\Delta A′B′C′\) son tres veces más grandes que\(\Delta ABC\).

Revisar

Dado\(A\) y\(A′\), encontrar el factor de escala. Se puede suponer que el centro de dilatación es el origen.

1. \(A(8,2), A′(12,3)\)
2. \(A(−5,−9), A′(−45,−81)\)
3. \(A(22,−7), A(11,−3.5)\)

El origen es el centro de dilatación. Dibujar la dilatación de cada figura, dado el factor de escala.

4. \(A(2,4), B(−3,7), C(−1,−2); k=3\)
5. \(A(12,8), B(−4,−16), C(0,10); k=34\)

Las preguntas de problemas de varios pasos 6-9 se construyen unas sobre otras.

6. Parcela\(A(1,2), B(12,4), C(10,10)\). Conéctate para formar un triángulo.
7. Hacer del origen el centro de dilatación. Dibuja 4 rayos desde el origen hasta cada punto desde #21. Entonces, trama\(A′(2,4), B′(24,8), C′(20,20)\). ¿Cuál es el factor de escala?
8. Utilizar\(k=4\), para encontrar\(A′′B′′C′′\). Trazar estos puntos.
9. ¿Cuál es el factor de escala de\(A′B′C′\) a\(A′′B′′C′′\)?

Si\(O\) es el origen, encuentra las siguientes longitudes (usando 6-9 arriba). Redondear todas las respuestas a la centésima más cercana.

10. \(OA\)
11. \(AA′\)
12. \(AA′′\)
13. \(OA′\)
14. \(OA′′\)
15. \(AB\)
16. \(A′B′\)
17. \(A′′B′′\)
18. Comparar las proporciones\(OA:OA′\) y\(AB: A′B′\). ¿Qué notas? ¿Por qué crees que es eso?
19. Comparar las proporciones\(OA:OA′′\) y\(AB: A′′B′′\). ¿Qué notas? ¿Por qué crees que es eso?

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.12.

El vocabulario

Término	Definición
Dilatación	Reducir o agrandar una figura según un factor de escala es una dilatación.
Fórmula de distancia	La distancia entre dos puntos\((x_1,y_1)\) y se\((x_2,y_2)\) puede definir como\(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\).
Mapeo	El mapeo es un procedimiento que implica el trazado de puntos en una cuadrícula de coordenadas para ver el comportamiento de una función.
Factor de Escala	Un factor de escala es una relación entre la escala y la dimensión original o real escrita en la forma más simple.

Recursos adicionales

Elemento interactivo

Video: Dilatación en el Plano Coordinado Principios - Básicos

Actividades: Dilatación en el Plano Coordinado Preguntas de Discusión

Ayudas de estudio: Guía de estudio de tipos de transformaciones

Práctica: Dilatación en el Plano Coordenado