7.18: Autosimilitud y Fractales
- Page ID
- 107415
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Una parte de un objeto se puede agrandar o encogerse para parecerse a todo el objeto.
Auto-Similaridad
Cuando una parte de un objeto se puede agrandar (o encogerse) para parecerse a todo el objeto, es autosimilar.
Para explorar la autosimilitud, pasaremos por algunos ejemplos. Normalmente, cada paso de un proceso se denomina iteración . El primer nivel se llama Etapa 0 .
¿Y si te dieran un objeto, como un triángulo o un copo de nieve, en el que una parte de él pudiera agrandarse (o encogerse) para parecerse a todo el objeto? ¿Cómo sería cada iteración sucesiva de ese objeto?
Ejemplo\(\PageIndex{1}\)
El triángulo Sierpinski itera un triángulo conectando los puntos medios de los lados y sombreando el triángulo central (Etapa 1). Repita este proceso para los triángulos sin sombra en la Etapa 1 para obtener la Etapa 2.
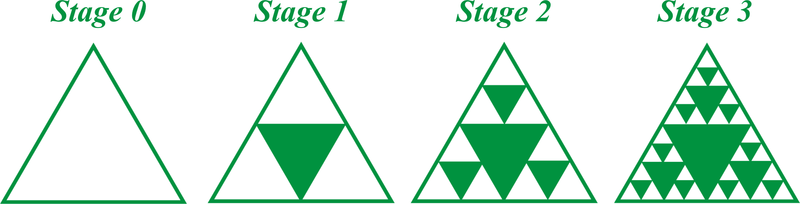
Ejemplo\(\PageIndex{2}\)
Determinar el número de triángulos sombreados y no sombreados en cada etapa del triángulo Sierpinkski. Determinar si hay un patrón.
| Etapa 0 | Etapa 1 | Etapa 2 | Etapa 3 | |
|---|---|---|---|---|
| Sin sombra | 1 | 3 | 9 | 27 |
| Sombreado | 0 | 1 | 4 | 13 |
Solución
El número de triángulos sin sombra parece ser potencias de\(3:\: 3^{0},\: 3^{1},\: 3^{2},\: 3^{3},\: ….\) El número de triángulos sombreados es la suma el número de triángulos sombreados y no sombreados de la etapa anterior. Por ejemplo, el número de triángulos sombreados en la Etapa 4 sería igual\(27 + 13 = 40\).
Ejemplo\(\PageIndex{3}\)
Al igual que el triángulo Sierpinski, un fractal es otro objeto autosimilar que se repite a escalas más pequeñas. A continuación se presentan las tres primeras etapas del copo de nieve de Koch.
Ejemplo\(\PageIndex{4}\)
Determinar el número de bordes y el perímetro de cada copo de nieve mostrado en el Ejemplo 3. Supongamos que la longitud de un lado del triángulo equilátero original (etapa 0) es 1.
| Etapa 0 | Etapa 1 | Etapa 2 | |
|---|---|---|---|
| Número de aristas | 3 | 12 | 48 |
| Largo de Borde | 1 | \(\dfrac{1}{3}\) | \(\dfrac{1}{9}\) |
| Perímetro | 3 | 4 | \(\dfrac{48}{9}=\dfrac{15}{3}\) |
Ejemplo\(\PageIndex{5}\)
El conjunto Cantor es otro ejemplo de un fractal. Consiste en dividir un segmento en tercios y luego borrar el tercio medio.
Revisar
- Dibuja la Etapa 4 del conjunto Cantor.
- Usa el Juego Cantor para rellenar la siguiente tabla.
| Número de Segmentos | Longitud de cada Segmento | Longitud total de los segmentos | |
|---|---|---|---|
| Etapa 0 | 1 | 1 | 1 |
| Etapa 1 | 2 | \(\dfrac{1}{3}\) | \(\dfrac{2}{3}\) |
| Etapa 2 | 4 | \(\dfrac{1}{9}\) | \(\dfrac{4}{9}\) |
| Etapa 3 | |||
| Etapa 4 | |||
| Etapa 5 |
- ¿Cuántos segmentos hay en Stage\(n\)?
- Dibuja la Etapa 3 del copo de nieve de Koch.
- Una variación del triángulo Sierpinski es la alfombra Sierpinski, que divide un cuadrado en 9 cuadrados iguales, coloreando solo el del medio. Después, divide los cuadrados incoloros para conseguir la siguiente etapa. Dibuja las primeras 3 etapas de este fractal.
- ¿Cuántos cuadrados coloreados vs. incoloros hay en cada etapa?
- Los fractales son muy comunes en la naturaleza. Por ejemplo, una hoja de helecho es un fractal. A medida que las hojas se acercan al final, se hacen cada vez más pequeñas. Encuentra otros tres ejemplos de fractales en la naturaleza.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.13.
vocabulario
| Término | Definición |
|---|---|
| auto-similar | Cuando una parte de un objeto se puede agrandar (o encogerse) para parecerse a todo el objeto. |
| Iteración | Una iteración es un solo paso dentro de un proceso. |
| punto medio | El punto medio de un segmento de línea es el punto del segmento de línea que divide el segmento en dos partes congruentes. |
Recursos adicionales
Elemento Interactivo
Video: Ejemplos de Auto-Similaridad - Básico
Actividades: Preguntas de discusión sobre la auto-similitud
Ayudas de estudio: Guía de estudio de autosimilitud
Práctica: Autosimilitud y Fractales
Mundo real: Fractales en todas partes