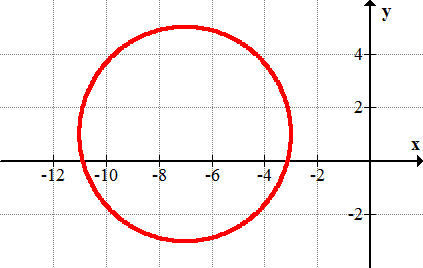9.3 Círculos
- Page ID
- 107433
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Un círculo es la colección de puntos que están a la misma distancia de un solo punto. ¿Cuál es la conexión entre el Teorema de Pitágoras y un círculo?
Graficando Círculos
El punto único del que todos los puntos de un círculo son equidistantes se llama el centro del círculo. Un círculo no tiene un foco o una directrix, en cambio simplemente tiene un centro. Los círculos pueden reconocerse inmediatamente a partir de la ecuación general de una cónica cuando los coeficientes de\(x^{2}\) y\(y^{2}\) son el mismo signo y el mismo valor. Los círculos no son funciones porque no pasan la prueba de línea vertical. La distancia desde el centro de un círculo hasta el borde del círculo se llama el radio del círculo. La distancia desde un extremo del círculo a través del centro hasta el otro extremo del círculo se llama diámetro. El diámetro es igual al doble del radio.
La forma gráfica de un círculo es:
\((x-h)^{2}+(y-k)^{2}=r^{2}\)
El centro del círculo está en\((h, k)\) y el radio del círculo es\(r\). Tenga en cuenta que esto se parece notablemente al Teorema de Pitágoras.
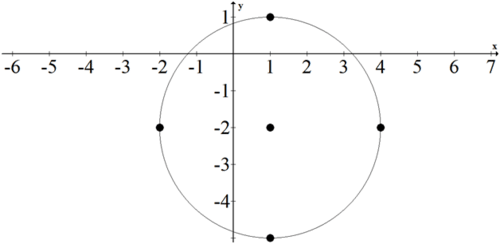
Para graficar un círculo, primero traza el centro y luego aplicar el radio. Tome la siguiente ecuación para un círculo:
\((x-1)^{2}+(y+2)^{2}=9\)
El centro está en (1, -2). Trazar ese punto y los cuatro puntos que están exactamente a 3 unidades del centro.
Ejemplos
Anteriormente, se le preguntó sobre la conexión entre los círculos y el Teorema de Pitágoras. La razón por la que la forma gráfica de un círculo se parece al Teorema de Pitágoras es porque cada una\(x\) y\(y\) coordenada a lo largo del exterior del círculo forma un triángulo rectángulo perfecto con el radio como la hipotenusa.
Grafica la siguiente cónica:\((x+2)^{2}+(y-1)^{2}=1\)
Convierte la siguiente ecuación en forma gráfica para un círculo. Identificar el centro y el radio.
\(36 x^{2}+36 y^{2}-24 x+36 y-275=0\)
Completar el cuadrado y luego dividir por el coeficiente de\(x^{2}\) y\(y^{2}\)
\(36 x^{2}-24 x+36 y^{2}+36 y=275\)
\(36\left(x^{2}-\frac{2}{3} x+\underline{-}\right)+36\left(y^{2}+y+\underline{x}\right)=275\)
\(36\left(x^{2}-\frac{2}{3} x+\frac{1}{9}\right)+36\left(y^{2}+y+\frac{1}{4}\right)=275+4+9\)
\(36\left(x-\frac{1}{3}\right)^{2}+36\left(y+\frac{1}{2}\right)^{2}=288\)
\(\left(x-\frac{1}{3}\right)^{2}+\left(y+\frac{1}{2}\right)^{2}=8\)
El centro es\(\left(\frac{1}{3},-\frac{1}{2}\right)\). El radio es\(\sqrt{8}=2 \sqrt{2}\).
Escribe la ecuación para el siguiente círculo.
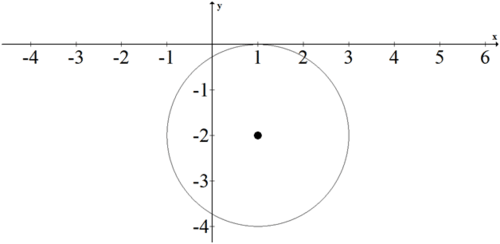
\((x-1)^{2}+(y+2)^{2}=4\)
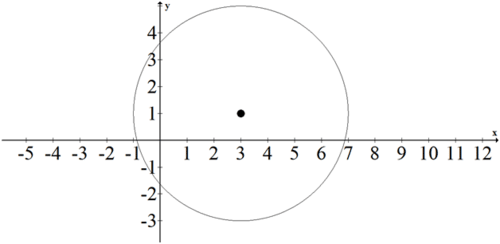
Escribe la ecuación del siguiente círculo.
El centro del círculo está en (3,1) y el radio del círculo es\(r=4\). La ecuación es\((x-3)^{2}+(y-1)^{2}=16\)
Grafica las siguientes conicas:
1. \((x+4)^{2}+(y-3)^{2}=1\)
2. \((x-7)^{2}+(y+1)^{2}=4\)
3. \((y+2)^{2}+(x-1)^{2}=9\)
4. \(x^{2}+(y-5)^{2}=8\)
5. \((x-2)^{2}+y^{2}=16\)
Traduzca las siguientes cónicas de la forma estándar a la forma gráfica.
6. \(x^{2}-4 x+y^{2}+10 y+18=0\)
7. \(x^{2}+2 x+y^{2}-8 y+1=0\)
8. \(x^{2}-6 x+y^{2}-4 y+12=0\)
9. \(x^{2}+2 x+y^{2}+14 y+25=0\)
10. \(x^{2}-2 x+y^{2}-2 y=0\)
Escribe las ecuaciones para los siguientes círculos.
11.
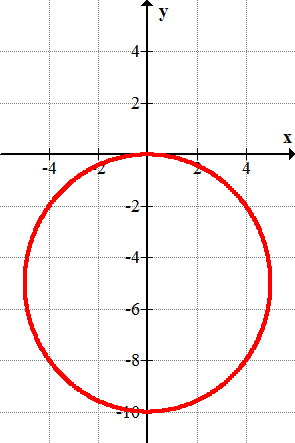
12.
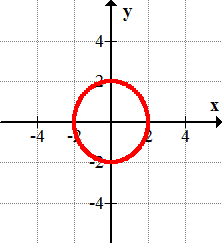
13.
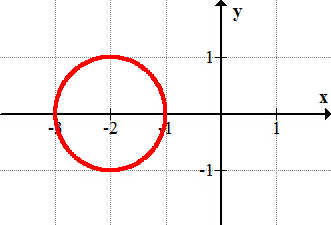
14.
15.
