9.5 Hipérbolas

Las hipérbolas son relaciones que tienen asíntotas. Al graficar funciones racionales a menudo se produce una hipérbola. En este concepto, las hipérbolas no se orientarán de la misma manera que con las funciones racionales, sino que la forma básica de una hipérbola seguirá estando ahí.

Las hipérbolas se pueden orientar para que se abran de lado a lado o de arriba a abajo. Uno de los errores más comunes que puedes cometer es olvidar de qué manera debe abrirse una hipérbola dada. ¿Cuáles son algunas estrategias para ayudar?

Graficando Hipérbolas

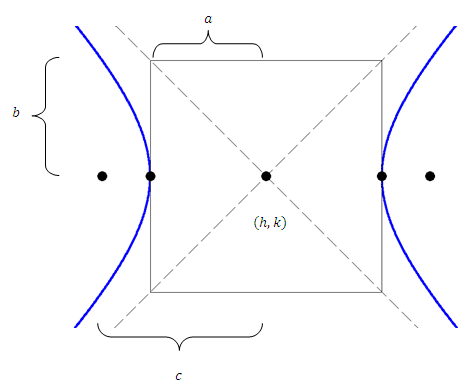
Una hipérbola tiene dos focos. Por cada punto de la hipérbola, la diferencia de las distancias a cada foco es constante. Esto es lo que define una hipérbola. La forma gráfica de una hipérbola que se abre de lado a lado es:

\(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\)

Una hipérbola que se abre arriba y abajo es:

\(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\)

Observe que para las hipérbolas,\(a\) va con el término positivo y\(b\) va con el término negativo. No importa qué constante es mayor.

Al graficar, las constantes\(a\) y le\(b\) permiten dibujar un rectángulo alrededor del centro. El eje transversal viaja de vértice a vértice y tiene longitud\(2 a\). El eje conjugado se desplaza perpendicular al eje transversal a través del centro y tiene longitud\(2 b\). Los focos se encuentran más allá de los vértices por lo que la excentricidad, que se mide como\(e=\frac{c}{a},\) es mayor que 1 para todas las hipérbolas. Las hipérbolas también tienen dos líneas directrix que están\(\frac{a^{2}}{c}\) alejadas del centro (no se muestran en la imagen).

El radio focal es\(a^{2}+b^{2}=c^{2}\)

Ejemplos

Ejemplo 1

Anteriormente, se le preguntó cómo determinar la dirección en la que se abre una hipérbola. La mejor estrategia para recordar en qué dirección abre la hipérbola suele ser la más simple. Considera la hipérbola\(x^{2}-y^{2}=1\). Esta hipérbola se abre de lado a lado porque claramente nunca\(x\) puede ser igual a cero. Este es un caso básico que demuestra que cuando lo negativo está con el\(y\) valor entonces la hipérbola se abre de lado a lado.

Ejemplo 2

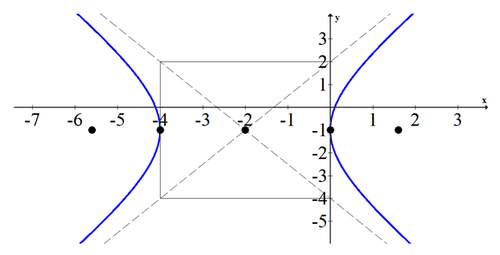
Ponga la siguiente hipérbola en forma gráfica, enumere los componentes y bosquéelo.

\(9 x^{2}-4 y^{2}+36 x-8 y-4=0\)

\(\begin{aligned} 9\left(x^{2}+4 x\right)-4\left(y^{2}+2 y\right) &=4 \\ 9\left(x^{2}+4 x+4\right)-4\left(y^{2}+2 y+1\right) &=4+36-4 \\ 9(x+2)^{2}-4(y+1)^{2} &=36 \\ \frac{(x+2)^{2}}{4}-\frac{(y+1)^{2}}{9} &=1 \end{aligned}\)

Forma: Hipérbola que se abre horizontalmente.

Centro: (-2, -1)

\(a=2\)

\(b=3\)

\(c=\sqrt{13}\)

\(e=\frac{c}{a}=\frac{\sqrt{13}}{2}\)

\(d=\frac{a^{2}}{c}=\frac{4}{\sqrt{13}}\)

Focos:\(\left(-2+\frac{\sqrt{13}}{2},-1\right),\left(-2-\frac{\sqrt{13}}{2},-1\right)\)

Vértices: (-4, -1), (0, -1)

Ecuaciones de asíntotas:\(\pm \frac{3}{2}(x+2)=(y+1)\)

Tenga en cuenta que es más fácil escribir las ecuaciones de las asíntotas en forma de punto-pendiente usando el centro y la pendiente.

Ecuaciones de las directivas:\(y=-2 \pm \frac{4}{\sqrt{13}}\)

Ejemplo 3

Encuentra la ecuación de la hipérbola con focos en (-3,5) y (9,5) y asíntotas con pendientes de\(\pm \frac{4}{3}\).

El centro se encuentra entre los focos en (3,5). El radio focal es\(c=6\). La pendiente de las asíntotas es siempre el ascenso sobre corrida dentro de la caja. En este caso ya que la hipérbola es horizontal y\(a\) está en la\(x\) dirección que está la pendiente\(\frac{b}{a}\). Esto hace un sistema de ecuaciones.

\(\frac{b}{a}=\pm \frac{4}{3}\)

\(a^{2}+b^{2}=6^{2}\)

Cuando resuelves, obtienes\(a=\sqrt{13}, b=\frac{4}{3} \sqrt{13}\).

\(\frac{(x-3)^{2}}{13}-\frac{(y-5)^{2}}{\frac{16}{9} \cdot 13}=1\)

Ejemplo 4

Encuentra la ecuación de la cónica que tiene un punto de enfoque en (1,2), una directriz en\(x=5\), y una excentricidad igual a\(\frac{3}{2}\). Utilice la propiedad de que la distancia desde un punto de la hipérbola al foco es igual a la excentricidad multiplicada por la distancia desde ese mismo punto a la directriz:

\(\overline{P F}=e \overline{P D}\)

Esta relación cierra la brecha entre elipses que tienen excentricidad menor que una e hipérbolas que tienen excentricidad mayor que una. Cuando la excentricidad es igual a uno,

forma es una parábola.

\(\sqrt{(x-1)^{2}+(y-2)^{2}}=\frac{3}{2} \sqrt{(x-5)^{2}}\)

Cuadrar ambos lados y reorganizar los términos para que se convierta en una hipérbola en forma gráfica.

\(\begin{aligned} x^{2}-2 x+1+(y-2)^{2} &=\frac{9}{4}\left(x^{2}-10 x+25\right) \\ x^{2}-2 x+1-\frac{9}{4} x^{2}+\frac{90}{4} x-\frac{225}{4}+(y-2)^{2} &=0\\-\frac{5}{4} x^{2}+\frac{92}{4} x+(y-2)^{2} &=\frac{221}{4}\\-5 x^{2}+92 x+4(y-2)^{2} &=221\\-5\left(x^{2}-\frac{92}{5} x\right)+4(y-2)^{2} &=221 \end{aligned}\)

\(\begin{aligned}-5\left(x^{2}-\frac{92}{5} x+\frac{92^{2}}{10^{2}}\right)+4(y-2)^{2} &=221-\frac{2116}{5}\\-5\left(x-\frac{92}{10}\right)^{2}+4(y-2)^{2} &=-\frac{1011}{5} \\\left(x-\frac{92}{10}\right)^{2}-(y-2)^{2} &=\frac{1011}{100} \\ \frac{\left(x-\frac{92}{10}\right)^{2}}{\left(\frac{1011}{100}\right)}-\frac{(y-2)^{2}}{\left(\frac{1011}{100}\right)} &=1 \end{aligned}\)

Ejemplo 5

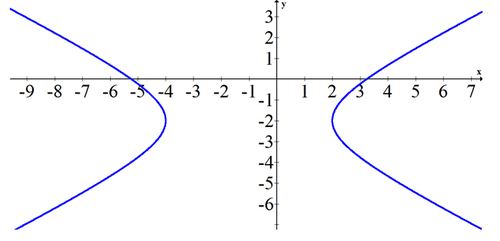
Dada la siguiente gráfica, estimar la ecuación de la cónica.

Dado que los puntos exactos no están marcados, deberá estimar la pendiente de las asíntotas para obtener una aproximación para\(a\) y\(b\). La pendiente parece estar a punto\(\pm \frac{2}{3}\). El centro parece estar en\((-1\), -2). El eje transversal es 6 lo que significa\(a=3\).

\(\frac{(x+1)^{2}}{9}-\frac{(y+2)^{2}}{4}=1\)

Revisar

Utilice la siguiente ecuación para #1 - #5:\(x^{2}+2 x-4 y^{2}-24 y-51=0\)

1. Pon la hipérbola en forma gráfica. Explica cómo sabes que es una hipérbola.

2. Identificar si la hipérbola se abre de lado a lado o de arriba a abajo.

3. Encuentra la ubicación de los vértices.

4. Encuentra las ecuaciones de las asíntotas.

5. Esbozar la hipérbola.

Utilice la siguiente ecuación para\(\# 6-\# 10:-9 x^{2}-36 x+16 y^{2}-32 y-164=0\)

6. Pon la hipérbola en forma gráfica. Explica cómo sabes que es una hipérbola.

7. Identificar si la hipérbola se abre de lado a lado o de arriba a abajo.

8. Encuentra la ubicación de los vértices.

9. Encuentra las ecuaciones de las asíntotas.

10. Esbozar la hipérbola.

Utilice la siguiente ecuación para #11 - #15:\(x^{2}-6 x-9 y^{2}-54 y-81=0\)

11. Pon la hipérbola en forma gráfica. Explica cómo sabes que es una hipérbola.

12. Identificar si la hipérbola se abre de lado a lado o de arriba a abajo.

13. Encuentra la ubicación de los vértices.

14. Encuentra las ecuaciones de las asíntotas.

15. Esbozar la hipérbola.