2.3.10: Valores exactos para seno inverso, coseno y tangente
- Page ID
- 107673
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Encuentra todos los ángulos en la unidad de círculo que coincidan con las proporciones exactas de
Estás trabajando con un corsé triangular en clase de taller. La abrazadera es un triángulo rectángulo, y la longitud de un lado del soporte es\(\sqrt{3}\approx 1.732\) y está conectada al otro lado en ángulo recto. La longitud del otro lado es 1. Necesitas encontrar el ángulo que hace la tercera pieza con la primera pieza, etiquetada a continuación como “C”:
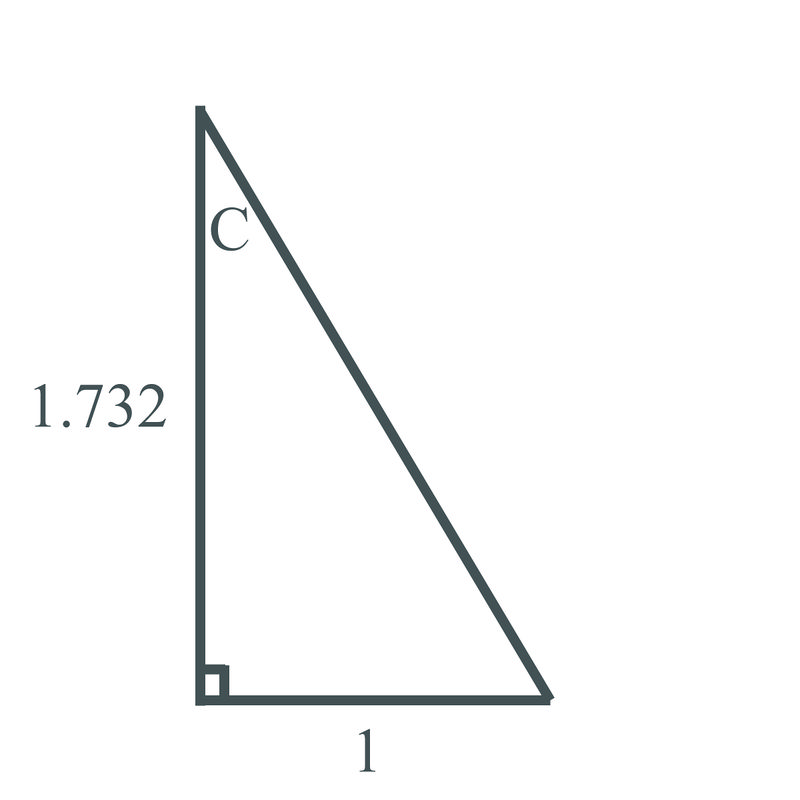
¿Puedes encontrar el ángulo entre las piernas del corsé?
Para cuando termines de leer esta lección, podrás responder a esta pregunta.
Inverso de seno, coseno y tangente
Las funciones trigonométricas inversas pueden ser útiles en una variedad de problemas matemáticos para encontrar ángulos que necesitas conocer. En muchos casos, como los ángulos que involucran múltiplos de\(30^{\circ}\),\(60^{\circ} \) y\(90^{\circ}\), los valores de las funciones trigonométricas a menudo se memorizan, ya que se usan con tanta frecuencia.
Recordemos el círculo unitario y los valores críticos. Con las funciones trigonométricas inversas, se puede encontrar el valor del ángulo (ya sea en radianes o grados) cuando se le da la relación y la función. Asegúrese de encontrar todas las soluciones dentro del intervalo dado.
Echemos un vistazo a algunos problemas de ejemplo.
1. Encuentra el valor exacto de la expresión sin calculadora, en\([0,2\pi )\).
\(\sin^{-1}\left(−\dfrac{\sqrt{3}}{2}\right)\)
Este es un valor de los triángulos rectos especiales y del círculo unitario.
Recordemos que\(−\dfrac{\sqrt{3}}{2}\) es del triángulo 30−60−90. El ángulo de referencia para el pecado y\(\dfrac{\sqrt{3}}{2}\) sería\(60^{\circ}\). Debido a que esto es seno y es negativo, debe estar en el tercer o cuarto cuadrante. La respuesta es\(\dfrac{4\pi }{3}\) o bien\(\dfrac{5\pi }{3}\).
2. Encuentra el valor exacto de la expresión sin calculadora, en\([0,2\pi )\).
\(\cos^{-1}\left(−\dfrac{\sqrt{2}}{2}\right)\)
Este es un valor de los triángulos rectos especiales y del círculo unitario.
\(−\dfrac{\sqrt{2}}{2}\)es de un triángulo rectángulo isósceles. El ángulo de referencia es entonces\(45^{\circ}\). Debido a que esto es coseno y negativo, el ángulo debe estar en el segundo o tercer cuadrante. La respuesta es\(\dfrac{3\pi }{4}\) o bien\(\dfrac{5\pi }{4}\).
3. Encuentra el valor exacto de la expresión sin calculadora, en\([0, 2\pi )\).
\(\tan^{-1}\sqrt{3}\)
Este es un valor de los triángulos rectos especiales y del círculo unitario.
\(\sqrt{3}\)es también de un triángulo 30−60−90. La tangente es\(\sqrt{3}\) para el ángulo de referencia\(60^{\circ}\). La tangente es positiva en el primer y tercer cuadrantes, por lo que la respuesta sería\(\dfrac{\pi}{3}\) o\(\dfrac{4\pi}{3}\).
Antes, se le pidió que encontrara el ángulo entre las piernas del corsé.
Solución
Usando su conocimiento de los valores de las funciones trigonométricas para los ángulos, puede trabajar hacia atrás para encontrar el ángulo que hace la abrazadera:
\(\begin{aligned} \tan C &=\dfrac{1}{\sqrt{3}} \\ \tan^{-1} C &=\tan^{-1}\dfrac{1}{\sqrt{3}} \\ C&=60^{\circ} \end{aligned}\)
Encuentra el valor exacto de la función inversa de\(\cos^{-1}(0)\), sin calculadora en\([0,2\pi)\)
Solución
\(\dfrac{\pi }{2}, \dfrac{3\pi}{2}\)
Encuentra el valor exacto de la función inversa de\(\tan^{-1}(−\sqrt{3})\), sin calculadora en\([0, 2\pi )\)
Solución
\(\dfrac{2\pi }{3}, \dfrac{5\pi }{3}\)
Encuentra el valor exacto de la función inversa de\(\sin^{-1}(−12)\), sin calculadora en\([0, 2\pi )\)
Solución
\(\dfrac{11\pi}{6}, \dfrac{7\pi}{6}\)
Revisar
Encuentra el valor exacto de cada expresión sin calculadora, en\([0, 2\pi )\).
- \(\sin^{-1}\left(\dfrac{\sqrt{2}}{2}\right)\)
- \(\cos^{-1}\left(\dfrac{1}{2}\right)\)
- \(\sin^{-1}(1)\)
- \(\cos^{-1}\left(−\dfrac{\sqrt{3}}{2}\right)\)
- \(\tan^{-1}\left(−\dfrac{\sqrt{3}}{3}\right)\)
- \(\tan^{-1}(−1)\)
- \(\sin^{-1}\left(\dfrac{\sqrt{3}}{2}\right)\)
- \(\cos^{-1}\left(\dfrac{\sqrt{2}}{2}\right)\)
- \(\csc ^{-1}(\sqrt{2})\)
- \(\sec ^{-1}(−2)\)
- \(\cot ^{-1}\left(\dfrac{\sqrt{3}}3\right)\)
- \(\sec ^{-1}\left(\dfrac{2\sqrt{3}}{2}\right)\)
- \(\csc ^{-1}\left(−\dfrac{2\sqrt{3}}{2}\right)\)
- \(\cot ^{-1}(−\sqrt{3})\)
- \(\cot ^{-1}(−1)\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.2.
El vocabulario
| Término | Definición |
|---|---|
| Inverso trigonométrico | Un inverso trigonométrico es una función que deshace una función trigonométrica para dar el argumento original de la función. También se puede utilizar para encontrar un ángulo faltante de un triángulo a partir de la relación de dos lados del triángulo. |
Recursos adicionales
Video: Ejemplos: Determinar Valores de Funciones Trigonométricas Usando Triángulos de Referencia
Práctica: Valores exactos para seno inverso, coseno y tangente