4.2.1: Fórmula de área para triángulos no rectos

Última actualización
Guardar como PDF

Page ID: 107608

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El área equivale a la mitad del producto de dos lados y el seno del ángulo incluido.

Fórmula alternativa para el área de un triángulo

Estás estudiando el Golfo de México en tu clase de Geografía. Tu Instructor plantea la idea del Triángulo de las Bermudas. Este es un lugar donde, según algunos, se pierden muchos aviones. Aquí hay una ilustración de ello:

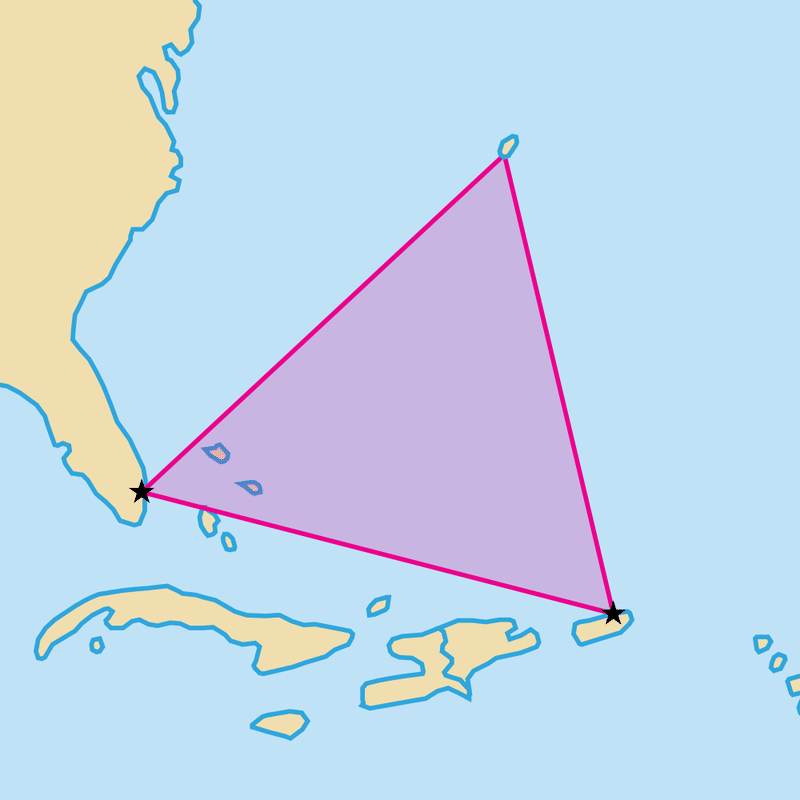
f-d_230c6d0da4c10ba84c9f27fe11a2b103553878342226baaef7b57d85+image_tiny+image_tiny.png — Figura\(\PageIndex{1}\)

Lo primero que esto te hace pensar es en tu clase de matemáticas, ya que esa clase es tu favorita. Te gustaría saber qué tan grande es el Triángulo de las Bermudas. Desafortunadamente, el Triángulo de las Bermudas no es un triángulo rectángulo. No obstante, sí sabes que la longitud de uno de los lados es de 950 millas, el otro lado es de 975 millas, y el ángulo entre ellos es\(60^{\circ} \).

¿Hay alguna forma de usar esta información para ayudarte a descubrir qué tan grande es el Triángulo de las Bermudas?

Área de un Triángulo

En Geometría, aprendiste que el área de un triángulo es\(A=\dfrac{1}{2} bh\), donde\(b\) está la base y h es la altura, o altitud.

Ahora que conoces las proporciones trigonométricas, esta fórmula se puede cambiar alrededor, usando seno.

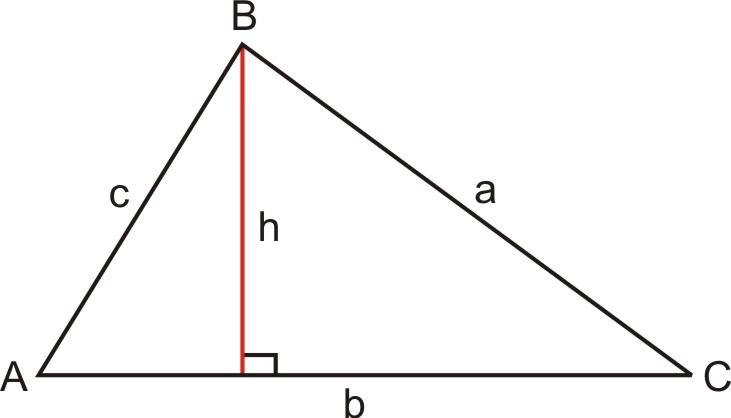
f-d_cc75c0d6c0fb4b9b54afb7191344e400be29c75a50744ad57a95904f+image_tiny+image_tiny.jpg — Figura\(\PageIndex{2}\)

Mirando el triángulo de arriba, puedes usar seno para determinar\(h\),\(\sin C=\dfrac{h}{a}\). Entonces, resolviendo esta ecuación para\(h\), tenemos\(a \sin C=h\). Sustituyendo esto por\(h\), ahora tenemos una nueva fórmula para área.

\(A=\dfrac{1}{2} ab \sin C\)

Lo que esto significa es que ya no necesitas la altura para encontrar el área. Todo lo que necesitas ahora son dos lados y el ángulo entre los dos lados, llamado el ángulo incluido.

Área de búsqueda

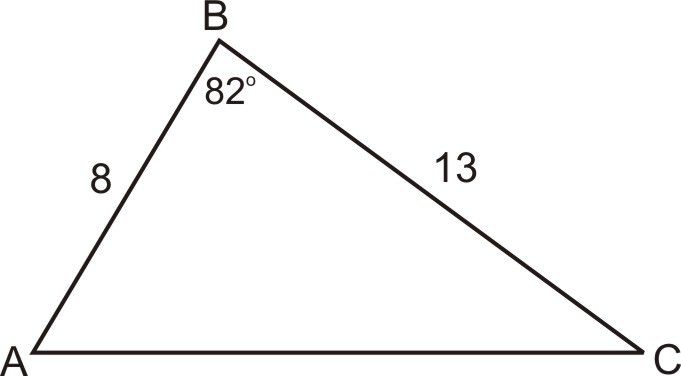
f-d_4b05c0f082c77aa5054fdfd715c132cb6a80f619a4eff748e532db1+image_tiny+image_tiny.jpg — Figura\(\PageIndex{3}\)

Usando la fórmula\(A=\dfrac{1}{2} ab \sin C\),, tenemos

\(\begin{aligned} A&=\dfrac{1}{2} \cdot 8\cdot 13\cdot \sin 82^{\circ} \\ &=4\cdot 13\cdot 0.990\\ &=51.494 \end{aligned}\)

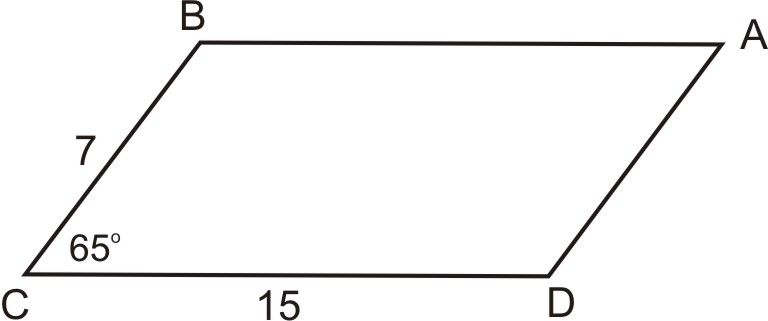
F-d_a1c4b8fd6d9a1648ae082406357361df607021867ac8e85d8a7e31e8+image_tiny+image_tiny.jpg — Figura\(\PageIndex{4}\)

Recordemos que un paralelogramo se puede dividir en dos triángulos. Entonces la fórmula para un paralelogramo, usando la nueva fórmula, sería:\(A=2\cdot \dfrac{1}{2} ab \sin C\) o\(A=ab \sin C\).

\(\begin{aligned} A&=7\cdot 15\cdot \sin 65^{\circ} \\&=95.162 \end{aligned} \)

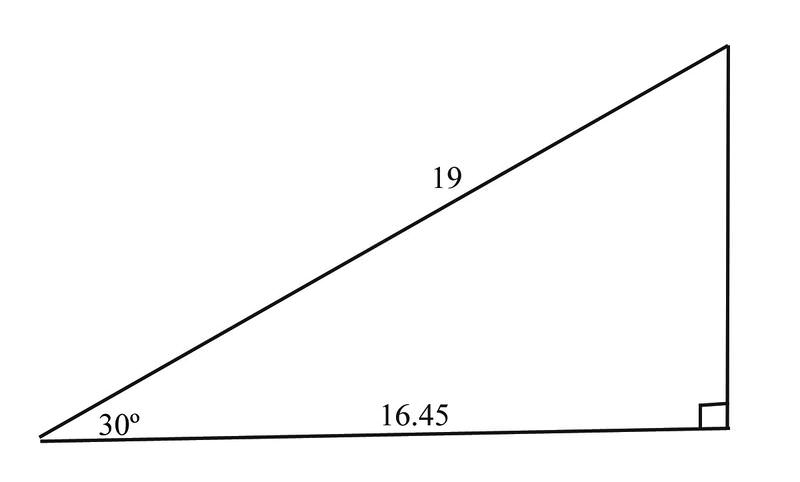
f-d_615ac6e69eced24c48eb387d55fe7270b0154b1b26c143fced7eb8+image_tiny+image_tiny.jpg — Figura\(\PageIndex{5}\)

Usando la fórmula\(A=\dfrac{1}{2} ab \sin C\),, tenemos

\(\begin{aligned} A&=\dfrac{1}{2} \cdot 16.45\cdot 19\cdot \sin 30^{\circ} \\ &=8.225\cdot 19\cdot 0.5 \\&=78.14\end{aligned}\)

Ejemplo\(\PageIndex{1}\)

Antes, te preguntaron qué tan grande es el Triángulo de las Bermudas.

Solución

Ahora que conoces la ecuación para el área de un triángulo en términos de dos de los lados y el ángulo incluido, podemos usar eso para resolver para el área del Triángulo de las Bermudas:

\(\begin{aligned} A&=\dfrac{1}{2} ab \sin\theta \\ A&=\dfrac{1}{2} (950)(975) \sin 60^{\circ} \\ A&=\dfrac{1}{2} (950)(975)(.866) \\ A&=401066.25\end{aligned}\)

El área del triángulo es de aproximadamente 401,006 millas cuadradas.

Ejemplo\(\PageIndex{2}\)

Encuentra el área del triángulo.

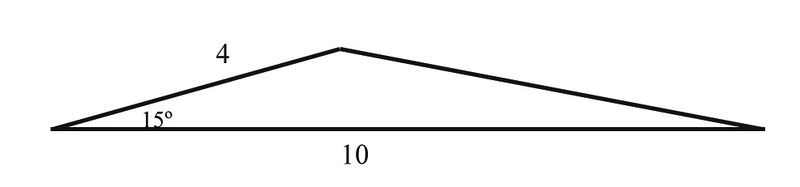
F-d_9daa59df286d734e460087ab792f1b13b8ce5a5a1295b05b0a038cb6+image_tiny+image_tiny.jpg — Figura\(\PageIndex{6}\)

Solución

Usando la fórmula\(A=\dfrac{1}{2} ab \sin C\),, tenemos

\(\begin{aligned} A&=\dfrac{1}{2} \cdot 4\cdot 10\cdot \sin 15^{\circ} \\ &=2\cdot 10\cdot 0.2589 \\ &=5.178 \end{aligned} \)

Ejemplo\(\PageIndex{3}\)

Encuentra el área del triángulo.

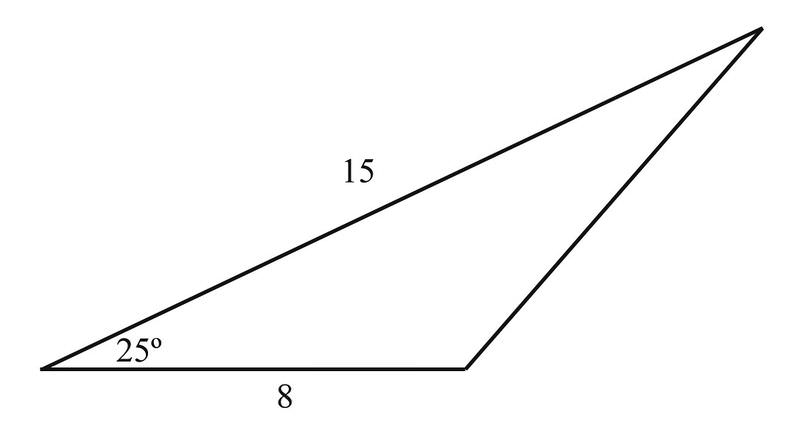
f-d_076a7990a2fb9bb16706f1c056724f42e4df51eaa1c793c02b13e617+image_tiny+image_tiny.jpg — Figura\(\PageIndex{7}\)

Solución

Usando la fórmula\(A=\dfrac{1}{2} ab \sin C\),, tenemos

\(\begin{aligned} A&=\dfrac{1}{2}\cdot 8\cdot 15\cdot \sin 25^{\circ} \\ &=4\cdot 15\cdot 0.4226\\ &=25.356 \end{aligned}\)

Ejemplo\(\PageIndex{4}\)

Encuentra el área del triángulo.

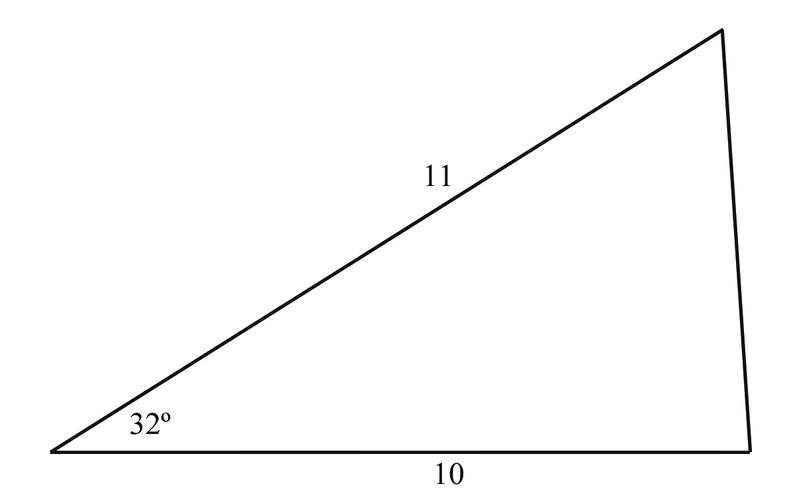
f-d_0a7473fb821537a58389db5eab483d2b09e0ae10e3ff0b2bafd60ae5+image_tiny+image_tiny.jpg — Figura\(\PageIndex{8}\)

Solución

Usando la fórmula\(A=\dfrac{1}{2} ab \sin C\),, tenemos

\(\begin{aligned} A&=\dfrac{1}{2} \cdot 10\cdot 11\cdot \sin 32^{\circ} \\&=5\cdot 11\cdot 0.53 \\ &=29.15 \end{aligned}\)

Revisar

Utilice la siguiente imagen para las preguntas 1 y 2.

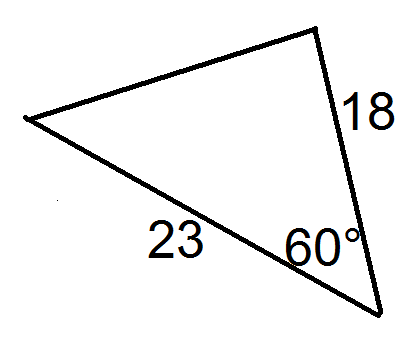
f-d_d7a9671bc150056da0a498d6c5677905213d4f70d1e12a6d82b25910+imagen_tiny+imagen_tiny.png — Figura\(\PageIndex{9}\)

Encuentra los valores de\(a\),\(b\), y\(C\) necesarios para la fórmula para encontrar el área del triángulo.
Ahora encuentra el área del triángulo.

Utilice la siguiente imagen para las preguntas 3 y 4.

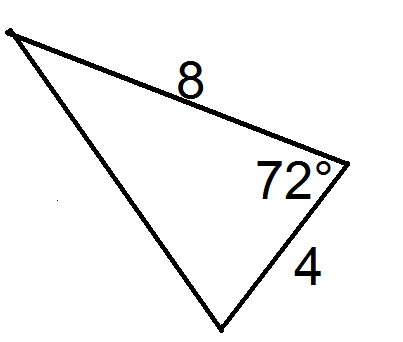
F-D_cedea896cdc514b74eaf10027059036b768b596fc594206408493d41+Image_Tiny+Image_Tiny.png — Figura\(\PageIndex{10}\)

Encuentra los valores de\(a\),\(b\), y\(C\) necesarios para la fórmula para encontrar el área del triángulo.
Ahora encuentra el área del triángulo.

Encuentra el área de cada triángulo a continuación.

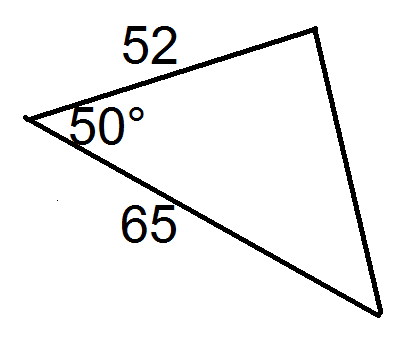
Figura\(\PageIndex{11}\)
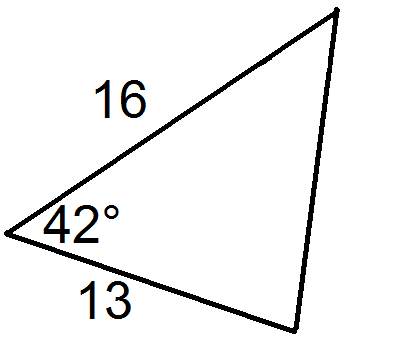
Figura\(\PageIndex{12}\)
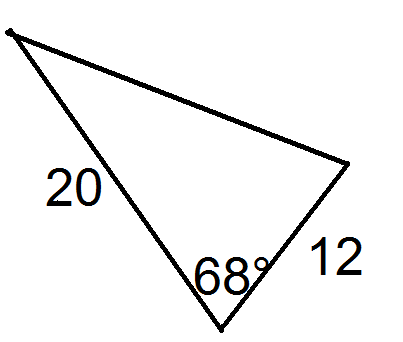
Figura\(\PageIndex{13}\)
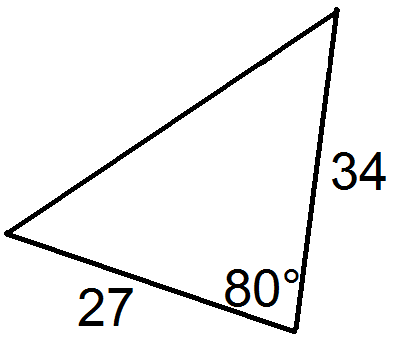
Figura\(\PageIndex{14}\)
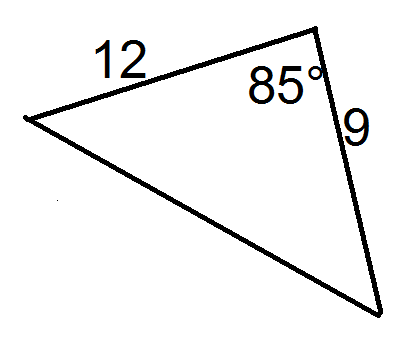
Figura\(\PageIndex{15}\)
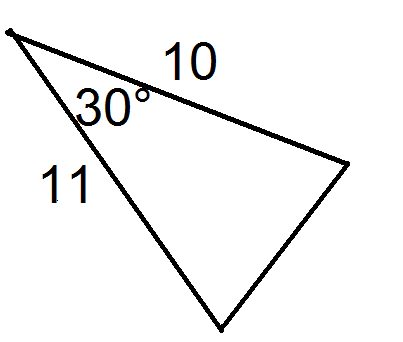
Figura\(\PageIndex{16}\)
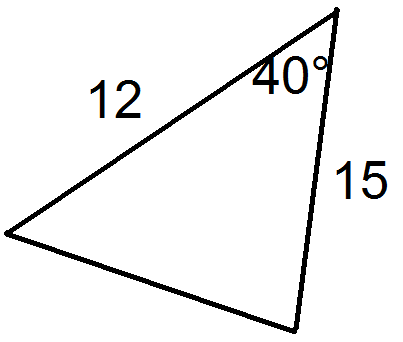
Figura\(\PageIndex{17}\)

Encuentra el área de cada paralelogramo.

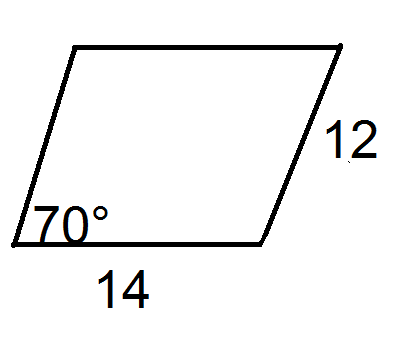
Figura\(\PageIndex{18}\)
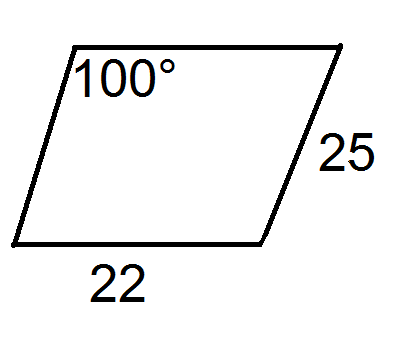
Figura\(\PageIndex{19}\)
Describe otra forma en la que podrías haber encontrado el área del paralelogramo en el problema anterior.
Cuando aprendiste por primera vez sobre el seno, aprendiste cómo funcionaba para los triángulos rectos. Explique por qué este método para calcular el área usa seno, pero funciona para triángulos no rectos.

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.12.

vocabulario

Término	Definición
Ángulo incluido	El ángulo incluido en un triángulo es el ángulo entre dos lados conocidos.
seno	El seno de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado opuesto al ángulo dado por la longitud de la hipotenusa.