3.3: Medidas de posición relativa
- Page ID
- 151795
Un alumno recibe una puntuación de 82 en un examen de mitad de período y le pregunta al instructor: “¿Qué tan bien me fue en la prueba?” Para responder a esta pregunta, necesitamos estadísticas que midan el ranking de esta calificación en relación con la clase. Estas estadísticas se denominan medida de posición relativa.
La puntuación z
Relacionado con la Regla Empírica es la z‐score que mide cuántas desviaciones estándar un punto de datos en particular está por encima o por debajo de la media. Las observaciones inusuales tendrían una puntuación z‐superior a 2 o inferior a ‐2. Las observaciones extremas tendrían puntuaciones z‐superiores a 3 o inferiores a ‐3 y deberían investigarse como posibles valores atípicos. Para un valor particular a partir de los datos (\(X_{i}\)), podemos calcular fácilmente la puntuación z para ese valor.
\[\text { Formula for z-score: } \quad z-\text { score }=\dfrac{X_{i}-\bar{X}}{s} \nonumber \]
Para el alumno que recibió un 82 en el examen podemos calcular el puntaje Z si conocemos la media muestral y la desviación estándar para la clase. Supongamos que para esta clase, la media muestral fue de 70 y la desviación estándar de la muestra fue de 10. Entonces para este alumno:
\[z-\text { score }=\dfrac{82-70}{10}=+1.2 \nonumber \]
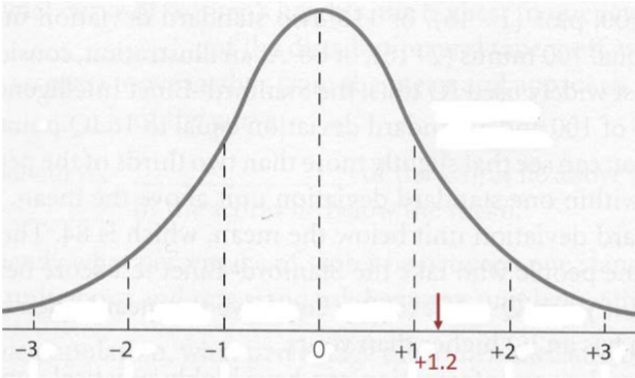
El puntaje z de 1.7 nos dice que la puntuación del estudiante estuvo muy por encima de la media, pero no muy inusual.
Interpretación de z‐score para varios alumnos
| Puntuación del examen | z‐score | Interpretación |
|---|---|---|
| 82 | +1.2 | muy por encima de la media |
| 66 | -0.4 | ligeramente por debajo de la media |
| 94 | +2.4 | inusualmente por encima de la media |
| 34 | -3.6 | extremadamente por debajo de la media |
Ejemplo: Comparando manzanas con naranjas
La media muestral para 100 manzanas Fuji fue 252 gramos y la desviación estándar fue de 55 gramos. La media muestral para 100 naranjas Navel fue de 286 gramos y la desviación estándar fue de 67 gramos. ¿Qué sería más inusual: una manzana pequeña que pesaba 130 gramos o una naranja grande que pesaba 430 gramos?
Solución
Algunas personas podrían decir “La manzana pequeña está 122 gramos por debajo de la media y la naranja grande está 144 gramos por encima de la media por lo que la naranja es más inusual”, pero esto no toma en cuenta la propagación de pesos para manzanas y naranjas. En cambio, debemos determinar qué puntaje z está más lejos de cero.
z‐score para manzana = (130 — 252) /55 = ‐2.22
z‐score para naranja = (430 — 286) /67 = +2.15
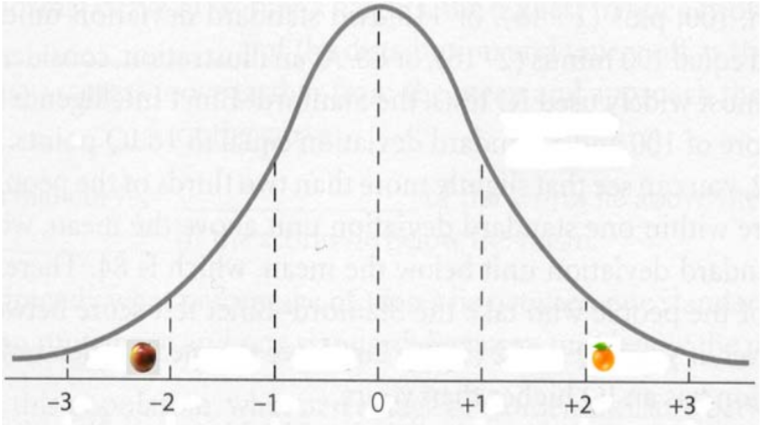
La manzana pequeña es un poco más inusual que la naranja grande porque ‐2.22 está más lejos de cero.
Percentil, cuartiles y rango intercuartil
En una sección anterior, exploramos cómo podemos usar la gráfica ogive para calcular percentiles y cuartiles para los datos. En esta sección se introducirá el percentil como medida de la posición relativa.
Definición: percentil p th
\(p^{th}\)Percentil ‐ el valor de los datos por debajo del cual cae el p por ciento de los datos.
Para calcular la ubicación del\(p^{th}\) percentil en una muestra de tamaño\(n\), utilice la fórmula:
\[p^{\text {th }} \text { percentile location }=p(n+1) \nonumber \]
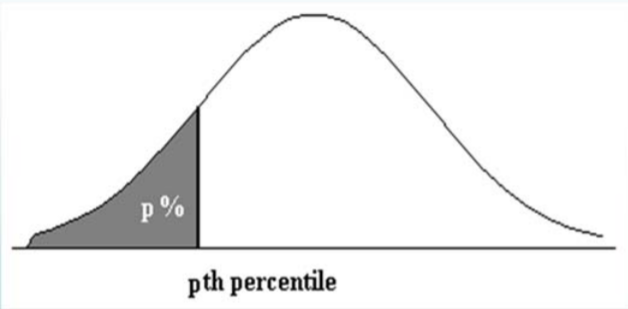
El\(25^{th}\) percentil también se conoce como el 1er Cuartil o Q1
El\(50^{th}\) percentil también se conoce como el 2do cuartil o mediana
El\(75^{th}\) percentil también se conoce como el 3er cuartil o Q3
Ejemplo: Estudiantes navegando por la web
Volvamos nuevamente al ejemplo de los minutos diarios que pasan en internet 30 estudiantes y utilicemos la regla empírica para encontrar el percentil 70.
Solución
Ubicación del\(70^{th}\) percentil = 0.70 (30+1) = 21.7 ≈ ubicación 22

\(70^{th}\)percentil ≈ 107 minutos.
Para un cálculo más preciso, puede utilizar la interpolación lineal de la parte fraccionaria de 21.7 agregando 30% de la ubicación 21 al 70% de la ubicación 22.

\(70^{th}\)percentil = (0.3) (105) + (0.7) (107) = 106.4 minutos
Existe un método alternativo para encontrar los cuartiles de datos.
- Encuentra la mediana (2do cuartil). La mediana divide los datos a la mitad.
- Q1 (1er cuartil) será la mediana de la primera mitad de los datos
- Q3 (3er cuartil) será la mediana de la segunda mitad de los datos.
Ejemplo: Estudiantes navegando por la web
Encuentra los tres cuartiles para estos datos.
Solución
Mediana = (101 +102) /2 = 101.5

Q1 = 1.er cuartil = 87

Q3 = 3er cuartil = 108

Intercuartil
Definición: Rango Intercuartil (IQR)
Una medida de variabilidad basada en el ranking de los datos se denomina Rango Intercuartil (IQR), que es la diferencia entre el tercer cuartil y el primer cuartil. El IQR representa el rango del 50% medio de los datos y representa la variabilidad de los datos con respecto a la mediana.
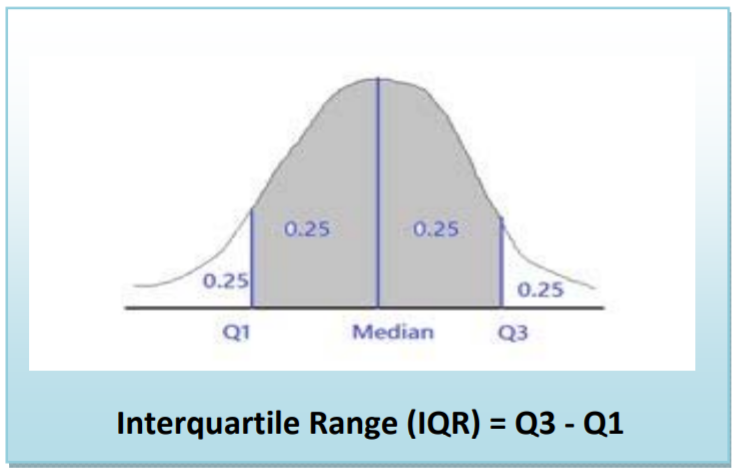
Ejemplo: Estudiantes navegando por la web
Encuentre y explique el rango intercuartílico para estos datos
Solución
IQR = 108 ‐87 = 21 minutos
El 50% medio de las observaciones se encuentran entre 87 y 108 minutos.


