3.2: Medidas de Variabilidad
- Page ID
- 151768
Al analizar los datos, también es importante describir la dispersión o variabilidad de los datos.
Ejemplo: Comparando altas temperaturas entre San Francisco y San Luis
Aquí están las altas temperaturas diarias para cada día en 2016 para las ciudades de San Francisco y San Luis. 272829
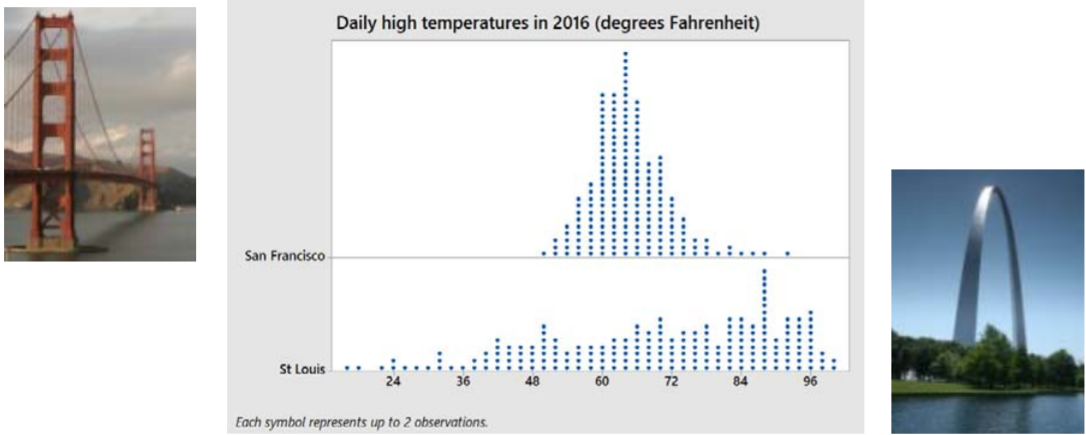
A pesar de que ambas ciudades parecen tener aproximadamente el mismo centro, es obvio que la propagación de las altas temperaturas diarias en San Francisco es mucho menor que en San Luis. Las temperaturas de San Francisco son en su mayoría suaves durante todo el año, mientras que San Luis tiene algunos días muy calurosos y muy fríos. En esta sección se explorarán las estadísticas que se utilizan para medir la variabilidad en los datos.
Rango
Definición: Rango
La medida de variabilidad más fácil de calcular es el rango de los datos.
Rango = valor máximo ‐ valor mínimo
Aquí están las temperaturas extremas altas en 2016 para San Francisco y San Luis.

El rango para las altas temperaturas de San Francisco es aproximadamente la mitad del rango para San Luis.
Ejemplo: Estudiantes navegando por la web
Volvamos al ejemplo de los minutos diarios que pasan en internet 30 estudiantes y encontremos la diferencia de los dos valores más extremos.

Rango = 125 ‐ 67 = 58 minutos
La ventaja de la gama es que es fácil de calcular. La principal desventaja es que el rango solo usa dos puntos y se ve extremadamente afectado por los valores atípicos. Por ejemplo, el 1 de septiembre de 2017 ¡San Francisco estableció un récord de temperatura alta de todos los tiempos de 106˚F! Si esto hubiera ocurrido en 2016, un valor atípico de 106˚F habría cambiado el rango para San Francisco de 42˚F a 56˚F, por lo que los estadísticos prefieren usar medidas de variabilidad que utilicen todos los datos, no simplemente los valores atípicos.
Varianza y Desviación Estándar
Los estadísticos quisieron desarrollar una medida de propagación que mostrara variabilidad con respecto al centro de los datos, llamarlo una “desviación promedio del centro”. Esta sección explorará las desviaciones de la media de la muestra y una sección posterior explorará la variabilidad con respecto a la mediana de la muestra.
Ejemplo: Entrega de pizza
Volvamos al ejemplo de pizza de Anthony's en el que una muestra de 5 entregas a cargo de un chofer demostró que el número total de pizzas entregadas en cada tirada fueron {2, 2, 5, 9, 12}. Recordemos que la media muestral X para estos datos fue 6, por lo que podemos calcular la desviación de la media muestral para cada punto:
|
Número de registro \(i\) |
Pizzas entregadas \(X_{i}\) |
Desviación de la media \(X_{i}-\bar{X}\) |
|---|---|---|
| \ (i\)” class="lt-estados-20839">1 | \ (X_ {i}\)” class="lt-stats-20839">2 | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">2 - 6 = - 4 |
| \ (i\)” class="lt-estados-20839">2 | \ (X_ {i}\)” class="lt-stats-20839">2 | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">2 - 6 = - 4 |
| \ (i\)” class="lt-estados-20839">3 | \ (X_ {i}\)” class="lt-stats-20839">5 | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">5 - 6 = -1 |
| \ (i\)” class="lt-estados-20839">4 | \ (X_ {i}\)” class="lt-stats-20839">9 | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">9 - 6 = +3 |
| \ (i\)” class="lt-estados-20839">5 | \ (X_ {i}\)” class="lt-stats-20839">12 | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">12 - 6 = +6 |
| \ (i\)” class="LT-STATS-20839">Total\(\sum\) | \ (X_ {i}\)” class="lt-stats-20839"> | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">0 |
La suma de las desviaciones de la media siempre será igual a cero, por lo que necesitamos una forma de calcular una desviación “promedio” de la media. Los estadísticos se dieron cuenta de que el signo de la desviación realmente no importa por lo que exploraron estadísticas como el valor absoluto de la desviación de la media:
|
Número de registro \(i\) |
Pizzas entregadas \(X_{i}\) |
Desviación de la media \(X_{i}-\bar{X}\) |
Valor absoluto de Desviación de la media \(\left|X_{i}-\bar{X}\right|\) |
|---|---|---|---|
| \ (i\)” class="lt-estados-20839">1 | \ (X_ {i}\)” class="lt-stats-20839">2 | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">2 - 6 = - 4 | \ (\ izquierda|X_ {i} -\ bar {X}\ derecha|\)” class="lt-stats-20839">4 |
| \ (i\)” class="lt-estados-20839">2 | \ (X_ {i}\)” class="lt-stats-20839">2 | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">2 - 6 = - 4 | \ (\ izquierda|X_ {i} -\ bar {X}\ derecha|\)” class="lt-stats-20839">4 |
| \ (i\)” class="lt-estados-20839">3 | \ (X_ {i}\)” class="lt-stats-20839">5 | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">5 - 6 = -1 | \ (\ izquierda|X_ {i} -\ bar {X}\ derecha|\)” class="lt-stats-20839">1 |
| \ (i\)” class="lt-estados-20839">4 | \ (X_ {i}\)” class="lt-stats-20839">9 | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">9 - 6 = +3 | \ (\ izquierda|X_ {i} -\ bar {X}\ derecha|\)” class="lt-stats-20839">3 |
| \ (i\)” class="lt-estados-20839">5 | \ (X_ {i}\)” class="lt-stats-20839">12 | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">12 - 6 = +6 | \ (\ izquierda|X_ {i} -\ bar {X}\ derecha|\)” class="lt-stats-20839">6 |
| \ (i\)” class="LT-STATS-20839">Total\(\sum\) | \ (X_ {i}\)” class="lt-stats-20839"> | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">0 | \ (\ izquierda|X_ {i} -\ bar {X}\ derecha|\)” class="lt-stats-20839">18 |
Dividiendo por el tamaño de la muestra, podemos encontrar que la “desviación absoluta promedio de la media” es 18/5 = 3.6 pizzas. Por razones que se explicarán en una sección posterior, no se encontró que esta medida fuera ideal.
Otro método para eliminar los signos negativos de los datos es cuadrar los números, ya que cualquier número negativo elevado a una potencia par se volverá positivo.
|
Número de registro \(i\) |
Pizzas entregadas \(X_{i}\) |
Desviación de la media \(X_{i}-\bar{X}\) |
Desviación cuadrada de la media \(\left(X_{i}-\bar{X}\right)^{2}\) |
|---|---|---|---|
| \ (i\)” class="lt-estados-20839">1 | \ (X_ {i}\)” class="lt-stats-20839">2 | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">2 - 6 = - 4 | \ (\ izquierda (X_ {i} -\ bar {X}\ derecha) ^ {2}\)” class="lt-stats-20839">16 |
| \ (i\)” class="lt-estados-20839">2 | \ (X_ {i}\)” class="lt-stats-20839">2 | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">2 - 6 = - 4 | \ (\ izquierda (X_ {i} -\ bar {X}\ derecha) ^ {2}\)” class="lt-stats-20839">16 |
| \ (i\)” class="lt-estados-20839">3 | \ (X_ {i}\)” class="lt-stats-20839">5 | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">5 - 6 = -1 | \ (\ izquierda (X_ {i} -\ bar {X}\ derecha) ^ {2}\)” class="lt-stats-20839">1 |
| \ (i\)” class="lt-estados-20839">4 | \ (X_ {i}\)” class="lt-stats-20839">9 | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">9 - 6 = +3 | \ (\ left (X_ {i} -\ bar {X}\ derecha) ^ {2}\)” class="lt-stats-20839">9 |
| \ (i\)” class="lt-estados-20839">5 | \ (X_ {i}\)” class="lt-stats-20839">12 | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">12 - 6 = +6 | \ (\ izquierda (X_ {i} -\ bar {X}\ derecha) ^ {2}\)” class="lt-stats-20839">36 |
| \ (i\)” class="LT-STATS-20839">Total\(\sum\) | \ (X_ {i}\)” class="lt-stats-20839"> | \ (X_ {i} -\ bar {X}\)” class="lt-estados-20839">0 | \ (\ izquierda (X_ {i} -\ bar {X}\ derecha) ^ {2}\)” class="lt-stats-20839">78 |
A la cantidad\(\sum\left(X_{i}-\bar{X}\right)^{2}=78\) se le llama la suma de las desviaciones cuadradas de la media. Para calcular una desviación cuadrada “promedio”, lo mejor es que la suma de las desviaciones cuadradas se divida por\(n‐1\) en lugar de por\(n\) (\(n\)es el tamaño de la muestra). Esta estadística se llama varianza de la muestra y se refiere por el símbolo\(s^2\).
\[\text { Sample Variance: } \quad s^{2}=\dfrac{\sum\left(X_{i}-\bar{X}\right)^{2}}{n-1} \nonumber \]
Podrías estar preguntando “Dado que esto es un promedio de desviaciones cuadradas, ¿por qué estamos dividiendo por\(n‐1\) en lugar de por\(n\)?” La razón es que\(\bar{X}\), la media muestral, utiliza los mismos datos\(X_{1}, X_{2}, \cdots, X_{n}\) para que puedas demostrar matemáticamente que solo necesitas conocer los\(n‐1\) puntos más la media muestral para determinar la varianza de la muestra. En estadística esto se llama\(n‐1\) grados de libertad, y se explorarán en una sección posterior.
Para los datos de pizza, la varianza de la muestra es:\(s^{2}=\dfrac{78}{5-1}=19.5\)
Aunque la varianza muestral utiliza todos los datos y mide la variabilidad a partir de la media, las unidades de este estadístico son cuadradas cuando las desviaciones son cuadradas. En nuestro ejemplo, la varianza muestral es de 19.5 pizzas‐cuadrado. Para resolver este problema, simplemente podemos tomar la raíz cuadrada de la varianza para volver a las unidades originales. Esta estadística se llama desviación estándar de la muestra y se representa con el símbolo\(s\).
\[\text { Sample Standard Deviation: } \quad s=\sqrt{\dfrac{\sum\left(X_{i}-\bar{X}\right)^{2}}{n-1}} \nonumber \]
Ejemplo: Comparando altas temperaturas entre San Francisco y San Luis
Calcular la varianza y desviación estándar manualmente es tedioso, por lo que utilizaremos la tecnología para calcular las estadísticas resumidas para las altas temperaturas diarias de 2016 en San Francisco y San Luis.

Los medios y las medianas muestran que en promedio San Luis es algo más cálido que San Francisco. Las varianzas y desviaciones estándar muestran que hay mucha más variabilidad en las altas temperaturas para San Luis, consistente con la gráfica de puntos que se muestra al inicio de esta sección.
Interpretación de la Desviación Estándar
Una estudiante me preguntó una vez sobre la distribución de la puntuación de un medio trimestre de estadística después de que vio su puntaje de 82 sobre 100. Le dije que la distribución de los puntajes de las pruebas tenía una puntuación media de 70 y una desviación estándar de 10. La mayoría de la gente tendría una comprensión intuitiva de la puntuación media como la “puntuación promedio del estudiante” y diría que a este estudiante le fue mejor que la media. Sin embargo, tener una comprensión intuitiva de la desviación estándar es más desafiante. Afortunadamente, hay una herramienta para ayudarnos.
La Regla Empírica (Regla 68 — 95 — 99.7)
La Regla Empírica es una herramienta útil para explicar la desviación estándar si tienes datos agrupados hacia la media y no fuertemente sesgados.
La desviación estándar es una medida de variabilidad o dispersión desde el centro de los datos tal como se define por la media.
Nota
La Regla Empírica establece que para los datos en forma de campana:
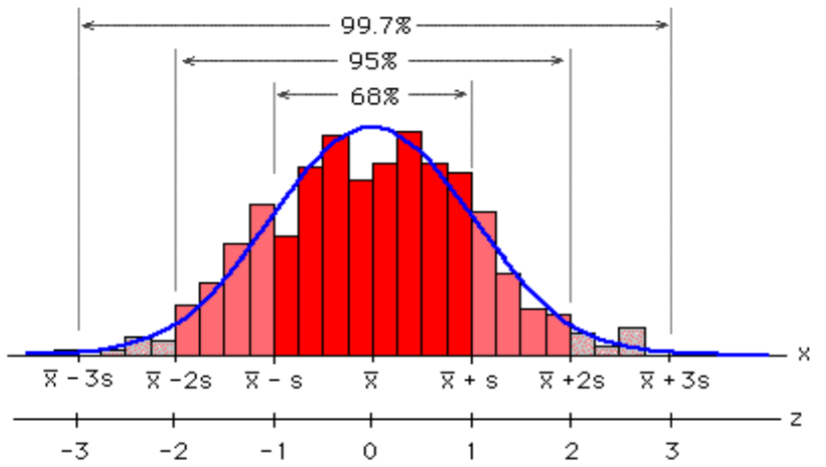
- El 68% de los datos se encuentra dentro de 1 desviación estándar de la media.
- El 95% de los datos se encuentra dentro de 2 desviaciones estándar de la media.
- El 99.7% de los datos se encuentra dentro de 3 desviaciones estándar de la media.
Aquí hay una interpretación de las calificaciones del examen para la clase en la que la media muestral fue 70 y la desviación estándar fue 10 usando la Regla Empírica.
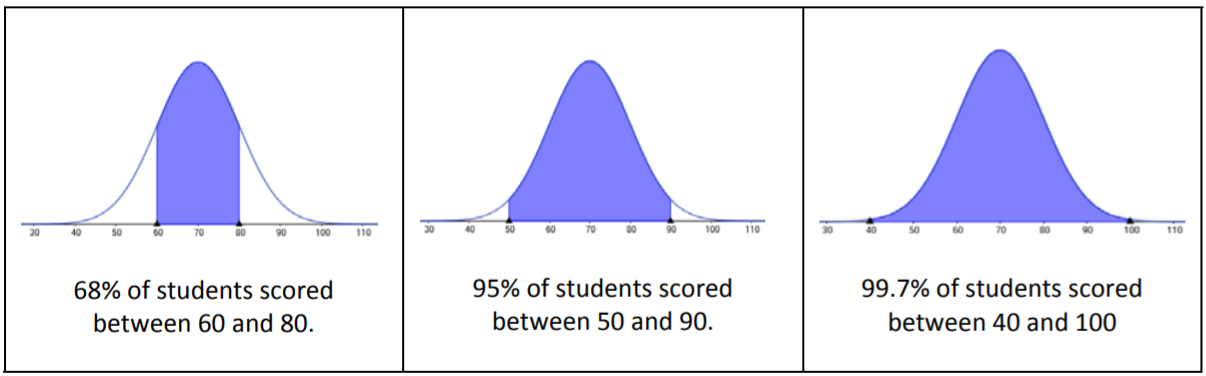
El alumno que obtuvo un 82 estaría en el 16% superior de la clase, más de una desviación estándar por encima de la puntuación media.
Ejemplo: Estudiantes navegando por la web
Volvamos al ejemplo de los minutos diarios que pasan en internet 30 estudiantes y utilicemos la regla empírica para encontrar valores entre los cuales se encuentran 68%, 95% y 99.7% de los datos. Comparar estos resultados con los resultados reales de los datos.

Recordemos que la forma de estos datos es ligeramente sesgada, pero los valores de datos se agrupan al centro. Veamos qué tan cerca está la Regla Empírica de los resultados reales.
Para usar la Regla Empírica, primero necesitamos calcular la media muestral y la desviación estándar.
\[\bar{X}=99.6 \quad s=14.7 \nonumber \]
La Regla Empírica dice que alrededor del 68% de los datos se encuentra dentro de 1 desviación estándar de la media, entre 84.9 y 114.3 minutos. El resultado real para los datos es 21/30 o 70% de los datos.
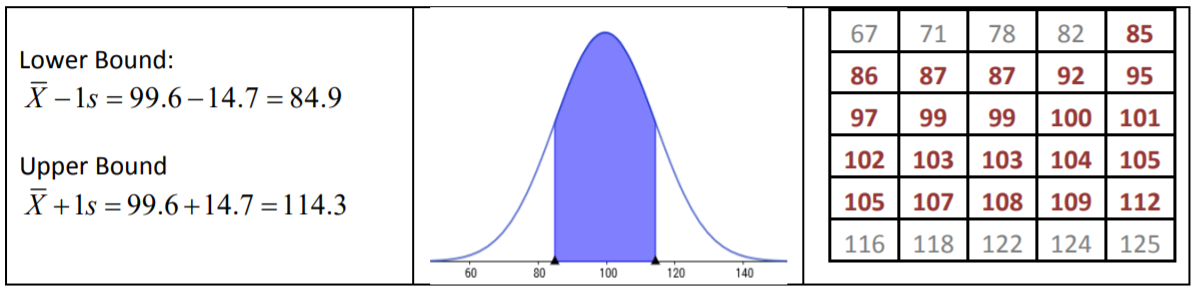
La Regla Empírica dice que alrededor del 95% de los datos se encuentran dentro de 2 desviaciones estándar de la media, entre 70.2 y 129.1 minutos. El resultado real para los datos es 29/30 o 96.7% de los datos.
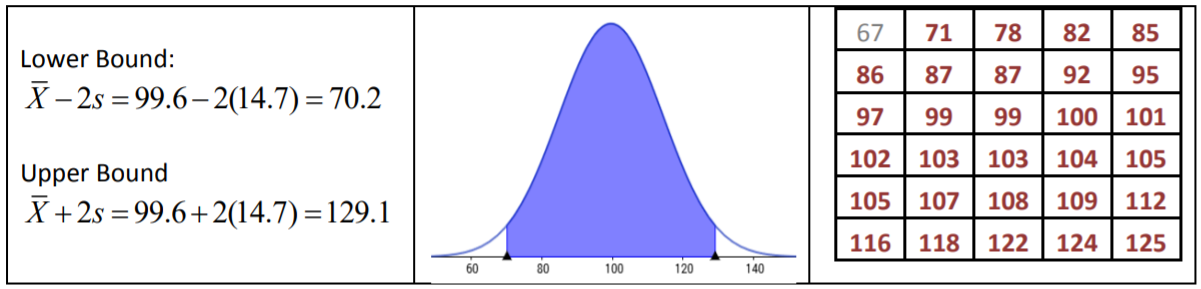
La Regla Empírica dice que alrededor del 99.7% de los datos se encuentran dentro de 3 desviaciones estándar de la media, entre 55.5 y 143.8 minutos. El resultado real para los datos es 30/30 o 100% de los datos.
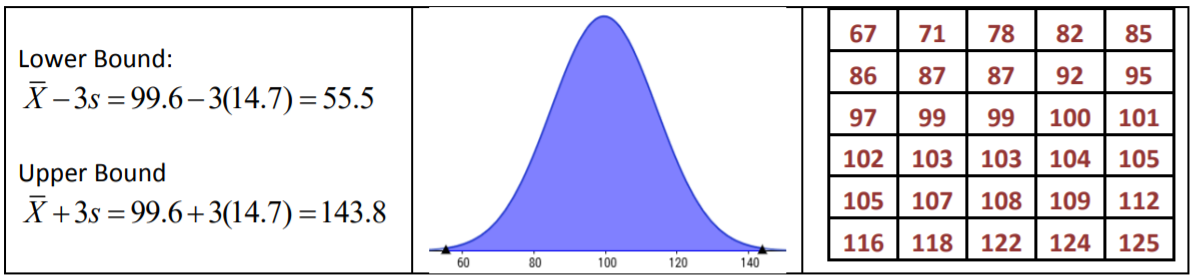
Entonces, aunque el tiempo en los datos de internet tiene cierta asimetría negativa, los porcentajes reales de datos dentro de 1, 2 y 3 desviaciones estándar de la media están cerca de los porcentajes de la Regla Empírica.
Usando el rango para estimar la desviación estándar de la muestra.
La Regla Empírica también da una regla muy rápida para hacer una estimación aproximada de la desviación estándar.
Estimación aproximada de la Desviación Estándar de la Muestra usando Rango
Para tamaños de muestra pequeños (entre 15 y 70): s ≈ Intervalo/4
Para tamaños de muestra intermedios (entre 70 y 500): s ≈ Intervalo/5
Para tamaños de muestra grandes (más de 500): s ≈ Intervalo/6
Ejemplo: Estudiantes navegando por la web
En el ejemplo previo del tiempo pasado en Internet por 30 estudiantes, determinamos que el Rango era de 58. Usando esta regla, estimaríamos la desviación estándar de la muestra en 58/4 = 14.5 minutos. Esta estimación aproximada es en realidad bastante cercana a la desviación estándar de la muestra calculada de 14.7 minutos.

Esta regla no debe usarse para determinar la desviación estándar real, sino que puede usarse para verificar la razonabilidad de una desviación estándar de muestra calculada o presentada.


