16.10: Cadenas de Confiabilidad en Tiempo Discreto
- Page ID
- 151968
La cadena de carreras de éxito
Supongamos que tenemos una secuencia de ensayos, cada uno de los cuales resulta en éxito o fracaso. Nuestra suposición básica es que si ha habido éxitos\( x \in \N \) consecutivos, entonces la probabilidad de éxito en el próximo juicio es\( p(x) \), independientemente del pasado, dónde\( p: \N \to (0, 1) \). Siempre que hay un fracaso, empezamos de nuevo, independientemente, con una nueva secuencia de ensayos. Lo suficientemente apropiado,\( p \) se llama la función de éxito. Vamos a\( X_n \) denotar la duración de la racha de éxitos después de\( n \) los ensayos.
\( \bs{X} =(X_0, X_1, X_2, \ldots) \)es una cadena de Markov de tiempo discreto con espacio de estado\( \N \) y matriz de probabilidad de transición\( P \) dada por\[ P(x, x + 1) = p(x), \; P(x, 0) = 1 - p(x); \quad x \in \N \] La cadena de Markov\( \bs{X} \) se llama la cadena de sucesiones.
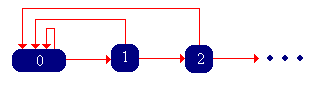
Ahora vamos a\( T \) denotar el número de juicio de la primera falla, comenzando con una nueva secuencia de ensayos. Tenga en cuenta que en el contexto de la cadena de sucesión-corridas\( \bs{X} \)\( T = \tau_0 \),, el primer tiempo de retorno al estado 0, comenzando en 0. Tenga en cuenta que\( T \) toma valores en\( \N_+ \cup \{\infty\} \), ya que presumiblemente, es posible que no se produzca ninguna falla. Y\( r(n) = \P(T \gt n) \) mucho\( n \in \N \), la probabilidad de al menos éxitos\( n \) consecutivos, comenzando con un nuevo conjunto de pruebas. Y\( f(n) = \P(T = n + 1) \) mucho\( n \in \N \), la probabilidad de éxitos exactamente\( n \) consecutivos, comenzando con un nuevo conjunto de senderos.
Las funciones\( p \),\( r \), y\( f \) se relacionan de la siguiente manera:
- \( p(x) = r(x + 1) \big/ r(x) \)para\( x \in \N \)
- \( r(n) = \prod_{x=0}^{n-1} p(x) \)para\( n \in \N \)
- \( f(n) = [1 - p(n)] \prod_{x=0}^{n-1} p(x) \)para\( n \in \N \)
- \( r(n) = 1 - \sum_{x=0}^{n-1} f(x) \)para\( n \in \N \)
- \( f(n) = r(n) - r(n + 1) \)para\( n \in \N \)
Así, las funciones\( p \),\( r \), y\( f \) dan información equivalente. Si conocemos una de las funciones, podemos construir las otras dos, y por lo tanto cualquiera de las funciones puede ser utilizada para definir la cadena de sucesiones. La función\( r \) es la función de confiabilidad asociada con\( T \).
La función\( r \) se caracteriza por las siguientes propiedades:
- \( r \)es positivo.
- \( r(0) = 1 \)
- \( r \)es estrictamente decreciente.
La función\( f \) se caracteriza por las siguientes propiedades:
- \( f \)es positivo.
- \( \sum_{x=0}^\infty f(x) \le 1 \)
Esencialmente,\( f \) es la función de densidad de probabilidad de\( T - 1 \), excepto que puede ser defectuosa en el sentido de que la suma de sus valores puede ser menor que 1. La probabilidad sobrante, por supuesto, es la probabilidad de que\( T = \infty \). Esta es la consideración crítica en la clasificación de la cadena de éxito-corridas, que consideraremos en breve.
Verifique que cada una de las siguientes funciones tenga las propiedades adecuadas y luego encuentre las otras dos funciones:
- \( p \)es una constante en\( (0, 1) \).
- \( r(n) = 1 \big/ (n + 1) \)para\( n \in \N \).
- \( r(n) = (n + 1) \big/ (2 \, n + 1) \)para\( n \in \N \).
- \( p(x) = 1 \big/ (x + 2) \)para\( x \in \N \).
Responder
- \( p(x) = p \)para\( x \in \N \). \( r(n) = p^n \)para\( n \in \N \). \( f(n) = (1 - p) p^n \)para\( n \in \N \).
- \( p(x) = \frac{x + 1}{x + 2} \)para\( x \in \N \). \( r(n) = \frac{1}{n + 1} \)para\( n \in \N \). \( f(n) = \frac{1}{n + 1} - \frac{1}{n} \)para\( n \in \N \).
- \( p(x) = \frac{(x + 2)(2 x + 1)}{(x + 1)(2 x + 3} \)para\( x \in \N \). \( r(n) = \frac{n + 1}{2 n + 1} \)para\( n \in \N \). \( f(n) = \frac{n + 1}{2 n + 1} - \frac{n + 2}{2 n + 3}\)para\( n \in \N \).
- \( p(x) = \frac{1}{x + 2} \)para\( x \in \N \). \( r(n) = \frac{1}{(n + 1)!} \)para\( n \in \N \). \( f(n) = \frac{1}{(n + 1)!} - \frac{1}{(n + 2)!} \)para\( n \in \N \).
En la parte a), señalar que los juicios son juicios de Bernoulli. Tenemos una app para este caso.
La aplicación Success-runs es una simulación de la cadena de sucesiones basada en ensayos de Bernoulli. Ejecute la simulación 1000 veces para varios valores\( p \) y varios estados iniciales, y anote el comportamiento general de la cadena.
La cadena de sucesiones es irreducible y aperiódica.
Prueba
La cadena es irreducible, ya que 0 conduce a cualquier otro estado, y cada estado vuelve a 0. La cadena es aperiódica desde entonces\( P(0, 0) \gt 0 \).
Recordemos que\( T \) tiene la misma distribución que\( \tau_0 \), el primer tiempo de retorno a 0 comenzando en el estado 0. Así, la clasificación de la cadena como recurrente o transitoria depende de\( \alpha = \P(T = \infty) \). Específicamente, la cadena de sucesiones es transitoria si\( \alpha \gt 0 \) y recurrente si\( \alpha = 0 \). Así, vemos que la cadena es recurrente si y sólo si es seguro que se producirá una falla. Podemos calcular el parámetro\( \alpha \) en términos de cada una de las tres funciones que definen la cadena.
En términos de\( p \)\( r \),\( f \), y\[ \alpha = \prod_{x=0}^\infty p(x) = \lim_{n \to \infty} r(n) = 1 - \sum_{x=0}^\infty f(x) \]
\( \alpha \)Calentar y determinar si la cadena de sucesiones de éxito\( \bs{X} \) es transitoria o recurrente para cada uno de los ejemplos anteriores.
Responder
- \( \alpha = 0 \), recurrente.
- \( \alpha = 0 \), recurrente.
- \( \alpha = \frac{1}{2} \), transitorio.
- \( \alpha = 0 \), recurrente.
Ejecutar la simulación de la cadena de sucesión-corridas 1000 veces para diversos valores de\( p \), comenzando en el estado 0. Anote los tiempos de regreso al estado 0.
Dejemos\( \mu = \E(T) \), el número de juicio esperado del primer fracaso, comenzando con una nueva secuencia de ensayos.
\( \mu \)se relaciona con\( \alpha \)\( f \), y de la\( r \) siguiente manera:
- Si\( \alpha \gt 0 \) entonces\( \mu = \infty \)
- Si\( \alpha = 0 \) entonces\( \mu = 1 + \sum_{n=0}^\infty n f(n) \)
- \( \mu = \sum_{n=0}^\infty r(n) \)
Prueba
- Si\( \alpha = \P(T = \infty) \gt 0 \) entonces\( \mu = \E(T) = \infty \).
- Si\( \alpha = 0 \), así que\( T \) toma valores adentro\( \N_+ \), entonces\( f \) es el PDF de\( T - 1 \), entonces\( \mu = 1 + \E(T - 1) \).
- Este es un resultado básico de la teoría general del valor esperado:\( \E(T) = \sum_{n=0}^\infty \P(T \gt n) \).
La cadena de sucesión-corridas\( \bs{X} \) es positiva recurrente si y solo si\( \mu \lt \infty \).
Prueba
Dado que\( T \) es el tiempo de retorno a 0, comenzando en 0, y dado que la cadena es irreducible, se deduce de la teoría general que la cadena es positiva recurrente si y sólo si\( \mu = \E(T) \lt \infty \).
Si\( \bs{X} \) es recurrente, entonces\( r \) es invariante para\( \bs{X} \). En el caso recurrente positivo, cuando\( \mu \lt \infty \), la distribución invariante tiene función de densidad de probabilidad\( g \) dada por\[ g(x) = \frac{r(x)}{\mu}, \quad x \in \N \]
Prueba
Si\( y \in \N_+ \) entonces del resultado anterior,\[(r P)(y) = \sum_{x=0}^\infty r(x) P(x, y) = r(y - 1) p(y - 1) = r(y)\] For\( y = 0 \), utilizando de nuevo el resultado anterior,\[(r P)(0) = \sum_{x=0}^\infty r(x) P(x, 0) = \sum_{x=0}^\infty r(x)[1 - p(x)] = \sum_{x=0}^\infty [r(x) - r(x)p(x)] = \sum_{x=0}^\infty [r(x) - r(x + 1)]\] Si la cadena es recurrente,\( r(n) \to 0 \) como\( n \to \infty \) así la última suma se contrae a\( r(0) = 1 \). Recordemos eso\( \mu = \sum_{n = 0}^\infty r(n) \). De ahí que si\( \mu \lt \infty \), para que la cadena sea recurrente positiva, la función\( g \) (que se acaba de\( r \) normalizar) es la PDF invariante.
Cuando\( \bs{X} \) es recurrente, sabemos por la teoría general que cualquier otra función invariante izquierda no negativa es un múltiplo no negativo de\( r \)
Determinar si la cadena de sucesiones de éxito\( \bs{X} \) es transitoria, recurrente nula o recurrente positiva para cada uno de los ejemplos anteriores. Si la cadena es recurrente positiva, encuentra la función de densidad de probabilidad invariante.
Responder
- \( \mu = \frac{1}{1 - p} \), recurrente positivo. \( g(x) = (1 - p) p^x \)para\( x \in \N \).
- \( \alpha = 0 \),\( \mu = \infty \), nulo recurrente.
- \( \alpha = \frac{1}{2} \), transitorio.
- \( \mu = e - 1 \), recurrente positivo. \( g(x) = \frac{1}{(e - 1)(x + 1)!} \)para\( x \in \N \).
De (a), la cadena de sucesiones correspondientes a los ensayos de Bernoulli con probabilidad de éxito\( p \in (0, 1) \) tiene la distribución geométrica en\( \N \)\( 1 - p \), con parámetro, como distribución invariante.
Ejecute la simulación de la cadena de ejecuciones de éxito 1000 veces para varios valores\( p \) y varios estados iniciales. Comparar la distribución empírica con la distribución invariante.
La cadena de vida restante
Considere un dispositivo cuyo tiempo (discreto) de falla\( U \) toma valores\( \N \), con función de densidad de probabilidad\( f \). Asumimos que\( f(n) \gt 0 \) para\( n \in \N \). Cuando el dispositivo falla, se reemplaza inmediatamente (e independientemente) por un dispositivo idéntico. Para\( n \in \N \), vamos a\( Y_n \) denotar el tiempo hasta el fallo del dispositivo que está en servicio en el momento\( n \).
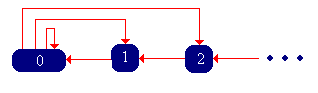
\( \bs{Y} = (Y_0, Y_1, Y_2, \ldots) \)es una cadena de Markov de tiempo discreto con espacio de estado\( \N \) y matriz de probabilidad de transición\( Q \) dada por\[ Q(0, x) = f(x), \; Q(x + 1, x) = 1; \quad x \in \N \]
La cadena de Markov\( \bs{Y} \) se llama la cadena de vida restante con función de densidad de probabilidad de vida útil\( f \), y tiene la gráfica de estado a continuación.
Tenemos una app para la cadena de vida restante cuya distribución de por vida es la distribución geométrica en\( \N \), con parámetro\( 1 - p \in (0, 1) \).
Ejecute la simulación de la cadena de vida restante 1000 veces para varios valores\( p \) y varios estados iniciales. Obsérvese el comportamiento general de la cadena.
Si\( U \) denota la vida útil de un dispositivo, como antes, tenga en cuenta que\( T = 1 + U \) es el tiempo de retorno a 0 para la cadena\( \bs{Y} \), comenzando en 0.
\( \bs{Y} \)es irreducible, aperiódica y recurrente.
Prueba
A partir de los supuestos en adelante\( f \), el estado 0 conduce a cualquier otro estado (incluyendo 0), y cada estado positivo conduce (determinísticamente) a 0. Así la cadena es irreducible y aperiódica. Por suposición,\( \P(U \in \N) = 1 \) así\( \P(T \lt \infty) = 1 \) y por lo tanto la cadena es recurrente.
Ahora vamos\( r(n) = \P(U \ge n) = \P(T \gt n) \) por\( n \in \N \) y vamos\( \mu = \E(T) = 1 + \E(U) \). Tenga en cuenta que\( r(n) = \sum_{x=n}^\infty f(x) \) y\( \mu = 1 + \sum_{x=0}^\infty f(x) = \sum_{n=0}^\infty r(n) \).
La cadena de sucesión-corridas\( \bs{X} \) es recurrente positiva si y solo si\( \mu \lt \infty \), en cuyo caso la distribución invariante tiene la función de densidad de probabilidad\( g \) dada por\[ g(x) = \frac{r(x)}{\mu}, \quad x \in \N \]
Prueba
Dado que la cadena es irreducible, es positiva recurrente si y solo si\( \mu = E(T) \lt \infty \). La función\( r \) es invariante para\( Q \): for\( y \in \N \)\ begin {align*} (r Q) (y) &=\ sum_ {x\ in\ N} r (x) Q (x, y) = r (0) Q (0, y) + r (y + 1) Q (y + 1, y)\\ &= f (y) + r (y + 1) = r (y)\ end {align*} En el caso recurrente positivo,\( \mu \) es la constante normalizadora para\( r \), entonces \( g \)es el PDF invariante.
Supongamos que\( \bs{Y} \) es la cadena de vida restante cuya distribución de vida útil es la distribución geométrica on\( \N \) con parámetro\( 1 - p \in (0, 1) \). Entonces esta distribución es también la distribución invariante.
Prueba
Por suposición,\( f(x) = (1 - p) p^x \) para\( x \in \N \), y la media de esta distribución es\( p / (1 - p) \). De ahí\( \mu = 1 + p / (1 - p) = 1 / (1 - p) \), y\( r(x) = \sum_{y = x}^\infty f(y) = p^x \) para\( x \in \N \). De ahí\( g = f \).
Ejecute la simulación de la cadena de ejecuciones de éxito 1000 veces para varios valores\( p \) y varios estados iniciales. Comparar la distribución empírica con la distribución invariante.
Reversión de tiempo
Probablemente ya hayas notado similitudes, en notación y resultados, entre la cadena de sucesiones y la cadena de vida restante. Hay conexiones más profundas.
Supongamos que\( f \) es una función de densidad de probabilidad on\( \N \) with\( f(n) \gt 0 \) for\( n \in \N \). \( \bs{X} \)Sea la cadena de éxito asociada\( f \) y\( \bs{Y} \) la cadena de vida restante asociada con\( f \). Entonces\( \bs{X} \) y\( \bs{Y} \) son las reversiones de tiempo el uno del otro.
Prueba
Bajo los supuestos sobre\( f \), ambas cadenas son recurrentes e irreducibles. De ahí que baste demostrar\[ r(x) P(x, y) = r(y) Q(y, x), \quad x, \, y \in \N \] que entonces seguirá que las cadenas son inversiones de tiempo unas de otras, y que\( r \) es una función invariante común (única hasta la multiplicación por constantes positivas). En el caso de que\( \mu = \sum_{n=0}^\infty r(n) \lt \infty \), la función\( g = r / \mu \) es el PDF invariante común. Sólo hay dos casos a considerar. Con\( y = 0 \), tenemos\( r(x) P(x, 0) = r(x)[1 - p(x)] \) y\( r(0) Q(y, 0) = f(x) \). Pero\( r(x) [1 - p(x)] = f(x) \) por el resultado anterior. Cuando\( x \in \N \) y\( y = x + 1 \), tenemos\( r(x) P(x, x + 1) = r(x) p(x) \) y\( r(x + 1) Q(x + 1, x) = r(x + 1) \). Pero\( r(x) p(x) = r(x + 1) \) por el resultado anterior.
En el contexto de la confiabilidad, también es fácil ver que las cadenas son inversiones de tiempo entre sí. Considere nuevamente un dispositivo cuya vida útil aleatoria toma valores\( \N \), con el dispositivo inmediatamente reemplazado por un dispositivo idéntico al fallar. Porque\( n \in \N \), podemos pensar en\( X_n \) como la antigüedad del dispositivo en servicio en el momento\( n \) y\( Y_n \) como el tiempo restante hasta la falla de ese dispositivo.
Ejecutar la simulación de la cadena de sucesión-corridas 1000 veces para diversos valores de\( p \), comenzando en el estado 0. Esta es la inversión temporal de la simulación en el próximo ejercicio
Ejecutar la simulación de la cadena de vida restante 1000 veces para diversos valores de\( p \), comenzando en el estado 0. Esta es la inversión temporal de la simulación en el ejercicio anterior.


