16.11: Cadena de Ramificación en Tiempo Discreto
- Page ID
- 151974
Teoría Básica
Introducción
Genéricamente, supongamos que tenemos un sistema de partículas que pueden generar o dividirse en otras partículas del mismo tipo. Aquí hay algunos ejemplos típicos:
- Las partículas son organismos biológicos que se reproducen.
- Las partículas son neutrones en una reacción en cadena.
- Las partículas son electrones en un multiplicador de electrones.
Suponemos que cada partícula, al final de su vida útil, es reemplazada por un número aleatorio de nuevas partículas a las que nos referiremos como hijos de la partícula original. Nuestra suposición básica es que las partículas actúan de forma independiente, cada una con la misma distribución de descendencia en\( \N \). Dejar\( f \) denotar la función de densidad de probabilidad común del número de crías de una partícula. También dejaremos\( f^{*n} = f * f * \cdots * f \) denotar el poder de convolución de grado\( n \) de\( f \); esta es la función de densidad de probabilidad del número total de hijos de\( n \) partículas.
Consideraremos la evolución del sistema en tiempo real en nuestro estudio de las cadenas de ramificación en tiempo continuo. En esta sección, estudiaremos la evolución del sistema en el tiempo generacional. Específicamente, las partículas con las que partimos están en la generación 0, y recursivamente, los hijos de una partícula en generación\( n \) están en generación\( n + 1 \).
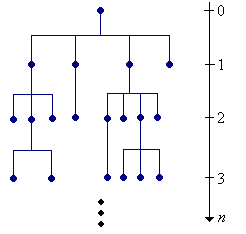
Dejar\( X_n \) denotar el número de partículas en generación\( n \in \N \). Una forma de construir el proceso matemáticamente es comenzar con una matriz de variables aleatorias independientes\( (U_{n,i}: n \in \N, \; i \in \N_+) \), cada una con función de densidad de probabilidad\( f \). Interpretamos\( U_{n,i} \) como el número de hijos de la partícula\( i \) th en generación\( n \) (si esta partícula existe). Tenga en cuenta que tenemos más variables aleatorias de las que necesitamos, pero esto no causa ningún daño, y sabemos que podemos construir un espacio de probabilidad que admita tal matriz de variables aleatorias. Ahora podemos definir nuestras variables de estado recursivamente mediante\[ X_{n+1} = \sum_{i=1}^{X_n} U_{n,i} \]
\( \bs{X} = (X_0, X_1, X_2, \ldots) \)es una cadena de Markov en tiempo discreto\( \N \) con matriz de probabilidad de transición\( P \) dada por\[ P(x, y) = f^{*x}(y), \quad (x, y) \in \N^2 \] La cadena\( \bs{X} \) es la cadena de ramificación con distribución de descendencia definida por\( f \).
Prueba
La propiedad de Markov y la forma de la matriz de transición siguen directamente de la construcción de las variables de estado dadas anteriormente. Como las variables\( (U_{n,i}: n \in \N, i \in \N_+) \) son independientes, cada una con PDF\( f \), tenemos\[ \P(X_{n+1} = y \mid X_0 = x_0, \ldots, X_{n-1} = x_{n-1}, X_n = x) = \P\left(\sum_{i=1}^x U_{n,i} = y\right) = f^{*x}(y) \]
La cadena de ramificación también se conoce como el proceso de Galton-Watson en honor a Francis Galton y Henry William Watson quienes estudiaron dichos procesos en el contexto de la supervivencia de los apellidos (aristocráticos). Obsérvese que los descendientes de cada partícula inicial forman una cadena de ramificación, y estas cadenas son independientes. Así, la cadena de ramificación que comienza con\( x \) partículas es equivalente a copias\( x \) independientes de la cadena de ramificación comenzando con 1 partícula. Esta característica resulta ser muy importante en el análisis de la cadena. Obsérvese también que 0 es un estado absorbente que corresponde a extinción. Por otro lado, la población puede crecer hasta el infinito, a veces llamada explosión. El cálculo de la probabilidad de extinción es uno de los problemas fundamentales en las cadenas de ramificación; esencialmente resolveremos este problema en la siguiente subsección.
Extinción y Explosión
El comportamiento de la cadena de ramificación en valor esperado es fácil de analizar. Vamos a\( m \) denotar la media de la distribución de la descendencia, para que\[ m = \sum_{x=0}^\infty x f(x) \] Note eso\( m \in [0, \infty] \). El parámetro\( m \) resultará ser de fundamental importancia.
Propiedades de valor esperado
- \( \E(X_{n+1}) = m \E(X_n) \)para\( n \in \N \)
- \( \E(X_n) = m^n \E(X_0) \)para\( n \in \N \)
- \( \E(X_n) \to 0 \)como\( n \to \infty \) si\( m \lt 1 \).
- \( \E(X_n) = \E(X_0) \)para cada\( n \in \N \) si\( m = 1 \).
- \( \E(X_n) \to \infty \)como\( n \to \infty \) si\( m \gt 1 \) y\( \E(X_0) \gt 0 \).
Prueba
Para la parte (a) utilizamos un argumento de condicionamiento y la construcción anterior. Porque\( x \in \N \), es\[ \E(X_{n+1} \mid X_n = x) = \E\left(\sum_{i=1}^x U_{n,i} \biggm| X_n = x\right) = \E\left(\sum_{i=1}^x U_{n,i}\right) = m x \] decir,\( \E(X_{n+1} \mid X_n) = m X_n \) entonces la\( \E(X_{n+1}) = \E\left[\E(X_{n+1} \mid X_n)\right] = m \E(X_n) \) Parte (b) se desprende de (a) y luego las partes (c), (d), y (e) siguen de (b).
La parte (c) es extinción en la media; la parte (d) es estabilidad en la media; y la parte (e) es explosión en la media.
Recordemos que el estado 0 es absorbente (no hay partículas), y de ahí\( \{X_n = 0 \text{ for some } n \in \N\} = \{\tau_0 \lt \infty\} \) es el evento de extinción (donde como de costumbre,\( \tau_0 \) es el tiempo del primer retorno a 0). Nos preocupa primordialmente la probabilidad de extinción, en función del estado inicial. Primero, sin embargo, haremos algunas observaciones simples y eliminaremos algunos casos triviales.
Supongamos que\( f(1) = 1 \), para que cada partícula sea reemplazada por una sola partícula nueva. Entonces
- Cada estado está absorbiendo.
- Las clases de equivalencia son los conjuntos singleton.
- Con probabilidad 1,\( X_n = X_0 \) por cada\( n \in \N \).
Prueba
Estas propiedades son obvias ya que\( P(x, x) = 1 \) para cada\( x \in \N \).
Supongamos\( f(0) \gt 0 \) que para que con probabilidad positiva, una partícula muera sin descendencia. Entonces
- Cada estado lleva a 0.
- Todo estado positivo es transitorio.
- Con probabilidad 1 ya sea\( X_n = 0 \) para algunos\( n \in \N \) (extinción) o\( X_n \to \infty \) como\( n \to \infty \) (explosión).
Prueba
- Tenga en cuenta que\( P(x, 0) = [f(0)]^x \gt 0 \) para\( x \in \N \), por lo que cada estado lleva a 0 en un solo paso.
- Esto se desprende de (a). Si\( x \in \N_+ \), entonces\( x \) conduce al estado absorbente 0 con probabilidad positiva. De ahí que un retorno a\( x \), comenzando en\( x \), no puede tener probabilidad 1.
- Esto se desprende de los apartados a) y b). Con probabilidad 1, cada estado positivo es visitado solo finitamente muchas veces. De ahí que las únicas posibilidades sean\( X_n = 0 \) para algunos\( n \in \N \) o\( X_n \to \infty \) como\( n \to \infty \).
Supongamos que\( f(0) = 0 \) y\( f(1) \lt 1 \), para que cada partícula sea reemplazada por al menos una partícula, y con probabilidad positiva, más de una. Entonces
- Todo estado positivo es transitorio.
- \( \P(X_n \to \infty \text{ as } n \to \infty \mid X_0 = x) = 1 \)para cada\( x \in \N_+ \), para que esa explosión sea cierta, comenzando con al menos una partícula.
Prueba
- Vamos\( x \in \N_+ \). Bajo los supuestos sobre\( f \), estado\( x \) conduce a algún estado\( y \gt x \) pero\( y \) no conduce de nuevo a\( x \). De ahí que con probabilidad positiva, la cadena que inicia en no\( x \) volverá a\( x \).
- Esto se desprende de (a) y que el hecho de que los estados positivos no conduzcan a 0.
Supongamos que\( f(0) \gt 0 \) y\( f(0) + f(1) = 1 \), para que con probabilidad positiva, una partícula muera sin descendencia, y con probabilidad 1, una partícula no sea reemplazada por más de una partícula. Entonces
- Cada estado lleva a 0.
- Todo estado positivo es transitorio.
- Con probabilidad 1,\( X_n = 0 \) para algunos\( n \in \N \), por lo que la extinción es cierta.
Prueba
- Como antes,\( P(x, 0) = [f(0)]^x \gt 0 \) para\( x \in \N \), así\( x \) lleva a 0 en un solo paso.
- Esto se desprende de (a) y el hecho de que 0 está absorbiendo.
- Bajo los supuestos sobre\( f \), estado\( x \) lleva al estado\( y \) solo si\( y \le x \). Por lo que esto se desprende de (a) y (b).
Así, el caso interesante es cuándo\( f(0) \gt 0 \) y\( f(0) + f(1) \lt 1 \), de manera que con probabilidad positiva, una partícula morirá sin descendencia, y también con probabilidad positiva, la partícula será reemplazada por más de una nueva partícula. Asumiremos estas condiciones para lo que resta de nuestra discusión. Por la clasificación estatal sobre todos los estados conducen a 0 (extinción). Denotaremos la probabilidad de extinción, comenzando con una partícula, por\[ q = \P(\tau_0 \lt \infty \mid X_0 = 1) = \P(X_n = 0 \text{ for some } n \in \N \mid X_0 = 1) \]
El conjunto de estados positivos\( \N_+ \) es una clase de equivalencia transitoria, y la probabilidad de extinción comenzando con\( x \in \N \) partículas es\[ q^x = \P(\tau_0 \lt \infty \mid X_0 = x) = \P(X_n = 0 \text{ for some } n \in \N \mid X_0 = x) \]
Prueba
Bajo los supuestos sobre\( f \), desde cualquier estado positivo la cadena puede mover 2 o más unidades a la derecha y una unidad a la izquierda en un solo paso. De ello se deduce que cada estado positivo conduce a cualquier otro estado positivo. Por otro lado, cada estado positivo lleva a 0, que es absorbente. Así,\( \N_+ \) es una clase de equivalencia transitoria.
Recordemos que la cadena de ramificación que comienza con\( x \in \N_+ \) partículas actúa como cadenas ramificadoras\( x \) independientes comenzando con una partícula. Así, la probabilidad de extinción comenzando con\( x \) partículas es\( q^x \).
El parámetro\( q \) satisface la ecuación\[ q = \sum_{x = 0}^\infty f(x) q^x \]
Prueba
Este resultado se deriva del condicionamiento en el primer estado. \[ q = \P(\tau_0 \lt \infty \mid X_0 = 1) = \sum_{x = 0}^\infty \P(\tau_0 \lt \infty \mid X_0 = 1, X_1 = x) \P(X_1 = x \mid X_0 = 1) \]Pero por la propiedad de Markov y el resultado anterior,\[ \P(\tau_0 \lt \infty \mid X_0 = 1, X_1 = x) = \P(\tau_0 \lt \infty \mid X_1 = x) = q^x \] y por supuesto\( \P(X_1 = x \mid X_0 = 1) = P(1, x) = f(x) \).
Así, la probabilidad de extinción a\( q \) partir de 1 partícula es un punto fijo de la función generadora de probabilidad\( \Phi \) de la distribución de descendencia:\[ \Phi(t) = \sum_{x=0}^\infty f(x) t^x, \quad t \in [0, 1] \] Además, a partir de la discusión general de probabilidades de golpeo en la sección sobre recurrencia y fugacidad,\( q \) es el menor número de este tipo en el intervalo\( (0, 1] \). Si la función de generación de probabilidad se\( \Phi \) puede calcular en forma cerrada, a veces se\( q \) puede calcular resolviendo la ecuación\( \Phi(t) = t \).
\( \Phi \)satisface las siguientes propiedades:
- \( \Phi(0) = f(0) \).
- \( \Phi(1) = 1 \).
- \( \Phi^\prime(t) \gt 0 \)por\( t \in (0, 1) \) lo que\( \Phi \) en el aumento en\( (0, 1) \).
- \( \Phi^{\prime \prime}(t) \gt 0 \)para\( t \in (0, 1) \) así\( \Phi \) en cóncavo hacia arriba en\( (0, 1) \).
- \( m = \lim_{t \uparrow 1} \Phi^\prime(t) \).
Prueba
Estas son propiedades básicas de la función generadora de probabilidad. Recordemos que la serie que define\( \Phi \) es una serie de potencia de aproximadamente 0 con radio de convergencia\( r \ge 1 \). Una función definida por una serie de potencias es infinitamente diferenciable dentro del intervalo abierto de convergencia, y los derivados se pueden calcular término por término. Entonces\ begin {alinear*}\ Phi^\ prime (t) &=\ sum_ {x=1} ^\ infty x f (x) t^ {x-1}\ gt 0,\ quad t\ in (0, 1)\\\ Phi^ {\ prime\ prime} (t) &=\ sum_ {x=2} ^\ infty x (x - 1) f (x) t^ {x - 2}\ gt 0,\ quad t\ in (0, 1)\ end {align*} Si\( r \gt 1 \) entonces\( m = \Phi^\prime(1) \). Si\( r = 1 \), el resultado límite es lo mejor que podemos hacer.
Nuestro principal resultado es el siguiente, y relaciona la probabilidad de extinción\( q \) y la media de la distribución de la descendencia\( m \).
La probabilidad de extinción\( q \) y la media de la distribución de la descendencia\( m \) se relacionan de la siguiente manera:
- Si\( m \le 1 \) entonces\( q = 1 \), entonces la extinción es cierta.
- Si\( m \gt 1 \) entonces\( 0 \lt q \lt 1 \), entonces hay una probabilidad positiva de extinción y una probabilidad positiva de explosión.
Prueba
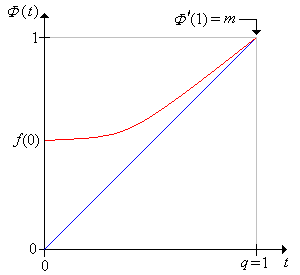
Figura\(\PageIndex{2}\): El caso de cierta extinción.
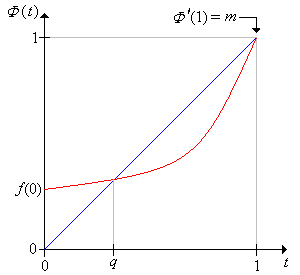
Figura\(\PageIndex{3}\): El caso de posible extinción y posible explosión.
Ejercicios Computacionales
Considere la cadena de ramificación con función de densidad de probabilidad de descendencia\( f \) dada por\( f(0) = 1 - p \)\( f(2) = p \),, donde\( p \in (0, 1) \) es un parámetro. Así, cada partícula muere o se divide en dos nuevas partículas. Encuentra cada uno de los siguientes.
- La matriz de transición\( P \).
- La media\( m \) de la distribución de la descendencia.
- La función generadora\( \Phi \) de la distribución de la descendencia.
- La probabilidad de extinción\( q \).
Contestar
Tenga en cuenta que una variable descendencia tiene la forma\( 2 I \) donde\( I \) es una variable indicadora con parámetro\( p \).
- Para\( x \in \N \),\( f^{* x} \) es el PDF de\( 2 U \) donde\( U \) tiene la distribución binomial con parámetros\( x \) y\( p \). De ahí\[ P(x, y) = f^{* x}(y) = \binom{x}{y/2} p^{y/2} (1 - p)^{x - y/2}, \quad y \in \{0, 2, \ldots, 2x\} \]
- \( m = 2 p \).
- \(\Phi(t) = p t^2 + (1 - p)\)para\( t \in \R \).
- \( q = 1 \)si\(0 \lt p \le \frac{1}{2} \) y\( q = \frac{1 - p}{p} \) si\( \frac{1}{2} \lt p \lt 1 \).


Considere la cadena de ramificación cuya distribución de descendencia es la distribución geométrica en\( \N \) con parámetro\( 1 - p \), donde\( p \in (0, 1) \). Así\( f(n) = (1 - p) p^n \) para\( n \in \N \). Encuentra cada uno de los siguientes:
- La matriz de transición\( P \).
- La media\( m \) de la distribución de la descendencia.
- La función generadora\( \Phi \) de la distribución de la descendencia.
- La probabilidad de extinción\( q \).
Contestar
- Para\( x \in \N \),\( f^{* x} \) es el PDF de la distribución binomial negativa on\( \N \) con parámetro\( 1 - p \). Entonces\[ P(x, y) = f^{* x}(y) = \binom{x + y - 1}{x - 1} p^y (1 - p)^x, \quad y \in \N \]
- \( m = \frac{p}{1 - p} \).
- \(\Phi(t) = \frac{1 - p}{1 - p t}\)para\( \left|t\right| \lt \frac{1}{p} \).
- \( q = 1 \)si\(0 \lt p \le \frac{1}{2} \) y\( q = \frac{1 - p}{p} \) si\( \frac{1}{2} \lt p \lt 1 \).


Curiosamente, la probabilidad de extinción es la misma que para el problema anterior.
Considere la cadena de ramificación cuya distribución de descendencia es la distribución de Poisson con parámetro\( m \in (0, \infty) \). Así\( f(n) = e^{-m} m^n / n! \) para\( n \in \N \). Encuentra cada uno de los siguientes:
- La matriz de transición\( P \).
- La media\( m \) de la distribución de la descendencia.
- La función generadora\( \Phi \) de la distribución de la descendencia.
- La probabilidad aproximada de extinción\( q \) cuándo\( m = 2 \) y cuándo\( m = 3 \).
Contestar
- Para\( x \in \N \),\( f^{* x} \) es el PDF de la distribución de Poisson con parámetro\( m x \). Entonces\[ P(x, y) = f^{* x}(y) = e^{-m x} \frac{(m x)^y}{y!}, \quad y \in \N \]
- El parámetro\( m \) es la media de la distribución de Poisson, por lo que la notación es consistente.
- \(\Phi(t) = e^{m (t - 1)}\)para\( t \in \R \).
- \( q = 1 \)si\(0 \lt m \le 1 \). Si\( m \gt 1 \) entonces\( q \) es la solución en\( (0, 1) \) de la ecuación\( e^{m (q - 1)} = q \) que se puede expresar en términos de una función especial conocida como la \( W \)función Lambert:\[ q = -\frac{1}{m} W\left(-m e^{-m}\right) \] For\( m = 2 \),\( q \approx 0.20319 \). Para\( m = 3 \),\( q \approx 0.059520 \).




