6.1: Variables aleatorias y Probabilidades
- Page ID
- 151150
Probabilidad asocia con un evento un número que indica la probabilidad de que ocurra ese evento en cualquier juicio. Un evento se modela como el conjunto de aquellos posibles resultados de un experimento que satisfacen una propiedad o proposición que caracteriza al evento.
A menudo, cada resultado se caracteriza por un número. Se realiza el experimento. Si el resultado se observa como una cantidad física, el tamaño de esa cantidad (en unidades prescritas) es la entidad realmente observada. En muchos casos no numéricos, es conveniente asignar un número a cada resultado. Por ejemplo, en un experimento de volteo de monedas, una “cabeza” puede estar representada por un 1 y una “cola” por un 0. En un juicio de Bernoulli, un éxito puede estar representado por un 1 y un fracaso por un 0. En una secuencia de ensayos, podemos estar interesados en el número de éxitos en una secuencia de ensayos\(n\) componentes. Se podría asignar un número distinto a cada carta en una baraja de naipes. Las observaciones del resultado de seleccionar una tarjeta podrían registrarse en términos de números individuales. En cada caso, el número asociado pasa a ser propiedad del resultado.
Variables aleatorias como funciones
Consideramos en este capítulo variables aleatorias reales (es decir, variables aleatorias de valor real). En el capítulo sobre Vectores Aleatorios y Distribuciones Conjuntas, extendemos la noción a cuantidades aleatorias valoradas por vector. La idea fundamental de una variable aleatoria real es la asignación de un número real a cada resultado elemental\(\omega\) en el espacio básico\(\Omega\). Tal asignación equivale a determinar una función\(X\), cuyo dominio es\(\Omega\) y cuyo rango es un subconjunto de la línea real R. Recordemos que una función de valor real en un dominio (digamos un intervalo\(I\) en la línea real) se caracteriza por la asignación de un número real\(y\) a cada elemento\(x\) (argumento) en el dominio. Para una función de valor real de una variable real, a menudo es posible escribir una fórmula o establecer de otra manera una regla que describa la asignación del valor a cada argumento. Excepto en casos especiales, no podemos escribir una fórmula para una variable aleatoria\(X\). Sin embargo, las variables aleatorias comparten algunas propiedades generales importantes de las funciones que desempeñan un papel esencial en la determinación de su utilidad.
Mapeos y mapeos inversos
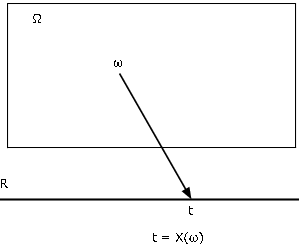
Existen diversas formas de caracterizar una función. Probablemente lo más útil para nuestros propósitos es como mapeo del dominio\(\Omega\) al codominio R. Encontramos el diagrama cartográfico de la Figura 1 extremadamente útil para visualizar los patrones esenciales. Variable aleatoria\(X\), como mapeo desde el espacio básico\(\Omega\) a la línea real R, asigna a cada elemento\(\omega\) un valor\(t = X(\omega)\). El punto objeto\(\omega\) es mapeado, o transportado, en el punto de imagen\(t\). Cada uno\(\omega\) se mapea en exactamente uno\(t\), aunque varios\(\omega\) pueden tener el mismo punto de imagen.
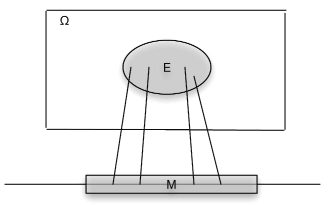
Asociados a una función\(X\) como mapeo están el mapeo inverso\(X^{-1}\) y las imágenes inversas que produce. \(M\)Déjese ser un conjunto de números en la línea real. Por la imagen inversa de\(M\) debajo del mapeo\(X\), nos referimos al conjunto de todos aquellos en los\(\omega \in \Omega\) que se mapean\(M\) por\(X\) (ver Figura 2). Si\(X\) no toma un valor en\(M\), la imagen inversa es el conjunto vacío (evento imposible). Si\(M\) incluye el rango de\(X\), (el conjunto de todos los valores posibles de\(X\)), la imagen inversa es todo el espacio básico\(\Omega\). Formalmente escribimos
\(X^{-1} (M) = \{\omega: X(\omega) \in M\}\)
Ahora asumimos que el conjunto\(X^{-1} (M)\), un subconjunto de\(\Omega\), es un evento para cada uno\(M\). Un examen detallado de esa afirmación es un tema en la teoría de medidas. Afortunadamente, los resultados de la teoría de medidas aseguran que podemos hacer la suposición para cualquier\(X\) subconjunto\(M\) de la línea real que probablemente se encuentre en la práctica. El conjunto\(X^{-1} (M)\) es el evento que\(X\) toma un valor en\(M\). Como evento, se le puede asignar una probabilidad.
Ejemplo\(\PageIndex{1}\) Some illustrative examples
- \(I_E\)donde\(E\) es un evento con probabilidad\(p\). Ahora\(X\) toma sólo dos valores, 0 y 1. El evento que\(X\) toma el valor 1 es el conjunto
\(\{\omega: X(\omega) = 1\} = X^{-1} (\{1\}) = E\)
así que eso\(P(\{\omega: X(\omega) = 1\}) = p\). Esta notación bastante torpe se acorta a\(P(X = 1) = p\). De igual manera,. Considera cualquier conjunto\(M\). Si ni 1 ni 0 está en\(M\), entonces\(X^{-1}(M) = \emptyset\) Si 0 está en\(M\), pero 1 no lo está, entonces\(X^{-1} (M) = E^c\) Si 1 está en\(M\), pero 0 no es, entonces\(X^{-1} (M) = E\) Si ambos 1 y 0 están en\(M\), entonces\(X^{-1} (M) = \Omega\) En este caso la clase de todos los eventos\(X^{-1} (M)\) consiste en evento\(E\), su complemento\(E^c\), el evento imposible\(\emptyset\), y el evento seguro\(\Omega\). - Consideremos una secuencia de ensayos de\(n\) Bernoulli, con probabilidad\(p\) de éxito. Dejar\(S_n\) ser la variable aleatoria cuyo valor es el número de éxitos en la secuencia de ensayos de\(n\) componentes. Entonces, según el análisis en la sección "Ensayos de Bernoulli y la Distribución Binomial"
\(P(S_n = k) = C(n, k) p^k (1-p)^{n - k}\)\(0 \le k \le n\)
Antes de considerar más ejemplos, observamos una propiedad general de las imágenes inversas. Lo declaramos en términos de una variable aleatoria, que se mapea\(\Omega\) a la línea real (ver Figura 3).
Preservación de operaciones de conjunto
Dejar\(X\) ser un mapeo de\(\Omega\) a la línea real R. Si\(M, M_i, i \in J\) son conjuntos de números reales, con respectivas imágenes inversas\(E\),\(E_i\), entonces
\(X^{-1} (M^c) = E^c\),\(X^{-1} (\bigcup_{i \in J} M_i) = \bigcup_{i \in J} E_i\) y\(X^{-1} (\bigcap_{i \in J} M_i) = \bigcap_{i \in J} E_i\)
El examen de ejemplos gráficos simples muestra la plausibilidad de estos patrones. Las pruebas formales equivalen a una lectura cuidadosa de la notación. En el centro de la estructura están los hechos de que cada elemento ω se mapea en un solo punto de imagen t y que la imagen inversa de\(M\) es el conjunto de todos aquellos\(\omega\) que se mapean en puntos de imagen en\(M\).
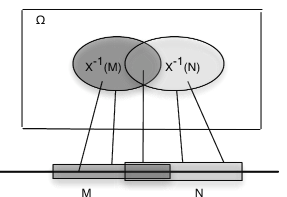
Una consecuencia fácil, pero importante, de los patrones generales es que las imágenes inversas de disjuntas también\(M, N\) son disjuntas. Esto implica que la inversa de una unión disjunta de\(M_i\) es una unión disjunta de las imágenes inversas separadas.
Ejemplo\(\PageIndex{2}\) Events determined by a random variable
Consideremos, nuevamente, la variable aleatoria\(S_n\) que cuenta el número de éxitos en una secuencia de ensayos de\(n\) Bernoulli. Dejar\(n = 10\) y\(p = 0.33\). Supongamos que queremos determinar la probabilidad\(P(2 < S_{10} \le 8)\). Vamos\(A_k = \{\omega: S_{10} (\omega) = k\}\), a lo que solemos acortar\(A_k = \{S_{10} = k\}\). Ahora la\(A_k\) forma una partición, ya que no podemos tener\(\omega \in A_k\) y\(\omega \in A_k\)\(j \ne k\) (es decir, para cualquiera\(\omega\), no podemos tener dos valores para\(S_n (\omega)\)). Ahora,
\(\{2 < S_{10} \le 8\} = A_3 \bigvee A_4 \bigvee A_5 \bigvee A_6 \bigvee A_7 \bigvee A_8\)
ya que\(S_{10}\) toma un valor mayor que 2 pero no mayor que 8 iff toma uno de los valores enteros de 3 a 8. Por la aditividad de la probabilidad,
Transferencia de masa y distribución de probabilidad inducida
Debido a la naturaleza abstracta del espacio básico y la clase de eventos, estamos limitados en los tipos de cálculos que se pueden realizar de manera significativa con las probabilidades en el espacio básico. Representamos la probabilidad como masa distribuida en el espacio básico y la visualizamos con la ayuda de diagramas generales de Venn y mapas minterm. Ahora pensamos en el mapeo de\(\Omega\) a R como una producción de una transferencia punto por punto de la masa de probabilidad a la línea real. Esto se puede hacer de la siguiente manera:
A cualquier conjunto\(M\) en la línea real asignar masa de probabilidad\(P_X(M) = P(X^{-1}(M))\)
Es evidente que\(P_X(M) \ge 0\) y\(P_X\) (R)\(= P(\Omega) = 1\). Y debido a la preservación de las operaciones de conjunto por el mapeo inverso
\(P_X(\bigvee_{i = 1}^{\infty} M_i) = P(X^{-1}(\bigvee_{i = 1}^{\infty} M_i)) = P(\bigvee_{i = 1}^{\infty} X^{-1}(M_i)) = \sum_{i = 1}^{\infty} P(X^{-1}(M_i)) = \sum_{i = 1}^{\infty} P_X(M_i)\)
Esto significa que\(P_X\) tiene las propiedades de una medida de probabilidad definidas en los subconjuntos de la línea real. Algunos resultados de la teoría de medidas muestran que esta probabilidad se define de manera única en una clase de subconjuntos de R que incluye cualquier conjunto normalmente encontrado en las aplicaciones. Hemos logrado una transferencia punto por punto del aparato de probabilidad a la línea real de tal manera que podemos hacer cálculos sobre la variable aleatoria\(X\). Llamamos a\(P_X\) la medida de probabilidad inducida por X. Su importancia radica en el hecho de que\(P(X \in M) = P_X(M)\). Así, para determinar la probabilidad de que la cantidad aleatoria X tome un valor en el conjunto M, determinamos cuánta masa de probabilidad inducida hay en el conjunto M. Esta transferencia produce lo que se denomina distribución de probabilidad para X. En el capítulo "Funciones de distribución y densidad “, consideramos formas útiles de describir la distribución de probabilidad inducida por una variable aleatoria. Pasamos primero a una clase especial de variables aleatorias.
Variables aleatorias simples
Consideramos, con cierto detalle, variables aleatorias que solo tienen un conjunto finito de valores posibles. Estas se llaman variables aleatorias simples. Así, el término “simple” se emplea en un sentido especial, técnico. La importancia de las variables aleatorias simples se basa en dos hechos. Por un lado, en la práctica podemos distinguir sólo un conjunto finito de valores posibles para cualquier variable aleatoria. Además, cualquier variable aleatoria puede aproximarse lo más cerca posible por una simple variable aleatoria. Cuando se ha examinado la estructura y propiedades de variables aleatorias simples, pasamos a casos más generales. Muchas propiedades de las variables aleatorias simples se extienden al caso general a través del procedimiento de aproximación.
Representación con la ayuda de funciones indicadoras
Para tratar las variables aleatorias simples de manera clara y precisa, debemos encontrar formas adecuadas de expresarlas analíticamente. Esto lo hacemos con la ayuda de funciones indicadoras. Se encuentran tres formas básicas de representación. Estos no son representantes mutuamente excluyentes.
Forma estándar o canónica, que muestra los valores posibles y los eventos correspondientes. Si X toma valores distintos
\(\{t_1, t_2, \cdot\cdot\cdot, t_n\}\)con probabilidades respectivas\(\{p_1, p_2, \cdot\cdot\cdot, p_n\}\)
y si\(A_i = \{X = t_i\}\), para\(1 \le i \le n\), entonces\(\{A_1, A_2, \cdot \cdot\cdot, A_n\}\) es una partición (es decir, en cualquier juicio, ocurre exactamente uno de estos eventos). A esto lo llamamos la partición determinada por (o, generada por) X. Podemos escribir
Si\(X(\omega) = t_i\), entonces\(\omega \in A_i\), para que\(I_{A_i} (\omega) = 1\) y todas las demás funciones del indicador tengan valor cero. La expresión de suma selecciona así el valor correcto\(t_i\). Esto es cierto para cualquiera\(t_i\), por lo que la expresión representa\(X(\omega)\) para todos\(\omega\). El conjunto distinto\(\{A, B, C\}\) de los valores y las probabilidades correspondientes\(\{p_1, p_2, \cdot\cdot\cdot, p_n\}\) constituyen la distribución para X. Los cálculos de probabilidad para X se realizan en términos de su distribución. Una de las ventajas de la forma canónica es que muestra el rango (conjunto de valores), y si\(\{A, B, C, D\}\) se conocen las probabilidades, se determina la distribución. Obsérvese que en forma canónica, si uno de los\(t_i\) tiene valor cero, incluimos ese término. Para algunas distribuciones de probabilidad puede ser que\(P(A_i) = 0\) para una o más de las\(t_i\). En ese caso, llamamos a estos valores valores nulos, pues solo pueden ocurrir con probabilidad cero, y por lo tanto son prácticamente imposibles. En la formulación general, incluimos posibles valores nulos, ya que no afectan ningún cálculo de probabilidad.
Ejemplo\(\PageIndex{3}\) Successes in Bernoulli trials
Como muestra el análisis de los ensayos de Bernoulli y la distribución binomial (ver Sección 4.8), la forma canónica debe ser
\(S_n = \sum_{k = 0}^{n} k I_{A_k}\)con\(P(A_k) = C(n, k) p^{k} (1-p)^{n - k}\),\(0 \le k \le n\)
Para muchos propósitos, tanto teórica como práctica, la forma canónica es deseable. Por un lado, muestra directamente el rango (es decir, conjunto de valores) de la variable aleatoria. La distribución consiste en el conjunto de valores\(\{t_k: 1 \le k \le n\}\) emparejados con el conjunto correspondiente de probabilidades\(\{p_k: 1 \le k \le n\}\), donde\(p_k = P(A_k) = P(X = t_k)\).
La variable aleatoria simple X puede ser representada por una forma primitiva
Observaciones
- Si\(\{C_j: 1 \le j \le m\}\) es una clase disjunta, pero\(\bigcup_{j = 1}^{m} C_j \ne \Omega\), podemos anexar el evento\(C_{m + 1} = [\bigcup_{j = 1}^{m} C_j]^c\) y asignarle valor cero.
- Decimos una forma primitiva, ya que la representación no es única. Cualquiera de los Ci puede ser particionado, con el mismo valor\(c_i\) asociado a cada subconjunto formado.
- La forma canónica es una forma primitiva especial. La forma canónica es única, y en muchos sentidos normativa.
Ejemplo\(\PageIndex{4}\) Simple random variables in primitive form
- Se hace girar una rueda dando, sobre una base igualmente probable, los números enteros del 1 al 10. \(C_i\)Sea el evento en el que la rueda se detenga\(i\),\(1 \le i \le 10\). Cada uno\(P(C_i) = 0.1\). Si los números 1, 4 o 7 suben, el jugador pierde diez dólares; si los números 2, 5 o 8 aparecen, el jugador no gana nada; si los números 3, 6 o 9 aparecen, el jugador gana diez dólares; si el número 10 aparece, el jugador pierde un dólar. La variable aleatoria que expresa los resultados puede expresarse en forma primitiva como
\(X = -10 I_{C_1} + 0 I_{C_2} + 10 I_{C_3} - 10 I_{C_4} + 0 I_{C_5} + 10 I_{C_6} - 10 I_{C_7} + 0 I_{C_8} + 10I_{C_9} - I_{C_{10}}\)
-
Una tienda tiene ocho artículos a la venta. Los precios son de $3.50, $5.00, $3.50, $7.50, $5.00, $5.00, $3.50 y $7.50, respectivamente. Entra un cliente. Ella compra uno de los artículos con probabilidades 0.10, 0.15, 0.15, 0.20, 0.10 0.05, 0.10 0.15. Se puede escribir la variable aleatoria que expresa el monto de su compra
\(X = 3.5 I_{C_1} + 5.0 I_{C_2} + 3.5 I_{C_3} + 7.5 I_{C_4} + 5.0 I_{C_5} + 5.0 I_{C_6} + 3.5 I_{C_7} + 7.5 I_{C_8}\)
Comúnmente tenemos X representado en forma afín, en la que la variable aleatoria se representa como una combinación afín de funciones indicadoras (es decir, una combinación lineal de las funciones indicadoras más una constante, que puede ser cero).
De esta forma, la clase no\(\{E_1, E_2, \cdot\cdot\cdot, E_m\}\) es necesariamente mutuamente excluyente, y los coeficientes no muestran directamente el conjunto de valores posibles. De hecho, los\(E_i\) suelen formar una clase independiente. OBSERVACIÓN. Cualquier forma primitiva es una forma afín especial en la que\(c_0 = 0\) y la\(E_i\) forma una partición.
Ejemplo\(\PageIndex{5}\)
Consideremos, nuevamente, la variable aleatoria\(S_n\) que cuenta el número de éxitos en una secuencia de ensayos de\(n\) Bernoulli. Si\(E_i\) es el evento de éxito en el\(i\) th juicio, entonces una forma natural de expresar el conteo es
\(S_n = \sum_{i = 1}^{n} I_{E_i}\), con\(P(E_i) = p\)\(1 \le i \le n\)
Esto es forma afín, con\(c_0 = 0\) y\(c_i =1\) para\(1 \le i \le n\). En este caso, los\(E_i\) no pueden formar una clase mutuamente excluyente, ya que forman una clase independiente.
Eventos generados por una simple variable aleatoria: forma canónica
Podemos caracterizar la clase de todas las imágenes inversas formadas por un simple aleatorio\(X\) en términos de la partición que determina. Considera cualquier conjunto\(M\) de números reales. Si\(t_i\) en el rango de\(X\) está en\(M\), entonces cada punto se\(\omega \in A_i\) mapea en\(t_i\), por lo tanto, en\(M\). Si el conjunto\(J\) es el conjunto de índices\(i\) tal que\(t_i \in M\), entonces
Sólo esos puntos\(\omega\) en\(A_M = \bigvee_{i \in J} A_i\) mapa en\(M\).
De ahí que la clase de eventos (es decir, imágenes inversas) determinada por\(X\) consiste en el evento imposible\(\emptyset\), el evento seguro\(\Omega\), y la unión de cualquier subclase de la\(A_i\) en la partición determinada por\(X\).
Ejemplo\(\PageIndex{6}\) Events determined by a simple random variable
Supongamos que la variable aleatoria simple\(X\) está representada en forma canónica por
\(X = -2I_A - I_B + 0 I_C + 3I_D\)
Entonces la clase\(\{A, B, C, D\}\) es la partición determinada por\(X\) y el rango de\(X\) es\(\{-2, -1, 0, 3\}\).
- Si\(M\) es el intervalo [-2, 1], los valores -2, -1 y 0 están en\(M\) y\(X^{-1}(M) = A \bigvee B \bigvee C\).
- Si\(M\) es el conjunto (-2, -1]\(\cup\) [1, 5], entonces los valores -1, 3 están en\(M\) y\(X^{-1}(M) = B \bigvee D\).
- El evento\(\{X \le 1\} = \{X \in (-\infty, 1]\} = X^{-1} (M)\), donde\(M = (- \infty, 1]\). Dado que los valores -2, -1, 0 están en\(M\), el evento\(\{X \le 1\} = A \bigvee B \bigvee C\).
Determinación de la distribución
Determinar la partición generada por una variable aleatoria simple equivale a determinar la forma canónica. Luego se completa la distribución determinando las probabilidades de cada evento\(A_k = \{X = t_k\}\).
De una forma primitiva
Antes de anotar el patrón general, consideramos un ejemplo ilustrativo.
Ejemplo\(\PageIndex{7}\) The distribution from a primitive form
Supongamos que se selecciona un elemento al azar de un grupo de diez elementos. Los valores (en dólares) y las probabilidades respectivas son
| \(c_j\) | 2.00 | 1.50 | 2.00 | 2.50 | 1.50 | 1.50 | 1.00 | 2.50 | 2.00 | 1.50 |
| \(P(C_j)\) | 0.08 | 0.11 | 0.07 | 0.15 | 0.10 | 0.09 | 0.14 | 0.08 | 0.08 | 0.10 |
Por inspección, encontramos cuatro valores distintos:\(t _ 1 = 1.00\),\(t_2 = 1.50\),\(t_3 = 2.00\), y\(t_4 = 2.50\). El valor 1.00 se toma para\(\omega \in C_7\), de modo que\(A_1 = C_7\) y\(P(A_1) = P(C_7) = 0.14\). Se toma el valor 1.50\(\omega \in C_2, C_5, C_6, C_{10}\) para que
\(A_2 = C_2 \bigvee C_5 \bigvee C_6 \bigvee C_{10}\)y\(P(A_2) = P(C_2) + P(C_5) + P(C_6) + P(C_{10}) = 0.40\)
Del mismo modo
\(P(A_3) = P(C_1) + P(C_3) + P(C_9) = 0.23\)y\(P(A_4) = P(C_4) + P(C_8) = 0.25\)
La distribución para X es así
| \(k\) | 1.00 | 1.50 | 2.00 | 2.50 |
| \(P(X = k)\) | 0.14 | 0.40 | 0.23 | 0.23 |
El procedimiento general podrá formularse de la siguiente manera:
Si\(X = \sum_{j = 1}^{m} c_j I_{c_j}\), identificamos el conjunto de valores distintos en el conjunto\(\{c_j: 1 \le j \le m\}\). Supongamos que estos son\(t_1 < t_2 < \cdot\cdot\cdot < t_n\). Para cualquier valor posible\(t_i\) en el rango, identificar el conjunto\(J_i\) de índices de aquellos\(j\) tales que\(c_j = t_i\) Luego los términos
\(\sum_{J_i} c_j I_{c_j} = t_i \sum_{J_i} I_{c_j} = t_i I_{A_i}\), donde\(A_i = \bigvee_j \in J_i C_j\),
y
\(P(A_i) = P(X = t_i) = \sum_{j \in J} P(C_j)\)
El examen de este procedimiento demuestra que existen dos fases:
- Seleccionar y ordenar los distintos valores\(t_1, t_2, \cdot\cdot\cdot, t_n\)
- Agregar todas las probabilidades asociadas a cada valor\(t_i\) para determinar\(P(X = t_i)\)
Utilizamos la función m-csort que realiza estas dos operaciones (ver Ejemplo 4 de “Mintterms y MATLAB Calculations”).
Ejemplo\(\PageIndex{8}\) Use of csort on Example 6.1.7
>> C = [2.00 1.50 2.00 2.50 1.50 1.50 1.00 2.50 2.00 1.50]; % Matrix of c_j
>> pc = [0.08 0.11 0.07 0.15 0.10 0.09 0.14 0.08 0.08 0.10]; % Matrix of P(C_j)
>> [X,PX] = csort(C,pc); % The sorting and consolidating operation
>> disp([X;PX]') % Display of results
1.0000 0.1400
1.5000 0.4000
2.0000 0.2300
2.5000 0.2300
Para un problema así de pequeño, el uso de una herramienta como csort no es realmente necesario. Pero en muchos problemas con grandes conjuntos de datos la función m csort es muy útil.
De forma afín
Supongamos que\(X\) está en forma afín,
\(X = c_0 + c_1 I_{E_1} + c_2 I_{E_2} + \cdot\cdot\cdot + c_m I_{E_m} = c_0 + \sum_{j = 1}^{m} c_j I_{E_j}\)
Determinamos una forma primitiva particular determinando el valor de\(X\) en cada minterm generado por la clase\(\{E_j: 1 \le j \le m\}\). Esto lo hacemos de manera sistemática utilizando vectores minterm y propiedades de funciones indicadoras.
\(X\)es constante en cada minterm generado por la clase\(\{E_1, E_2, \cdot\cdot\cdot, E_m\}\) ya que, como se observa en el tratamiento de la expansión minterm, cada función indicadora\(I_{E_i}\) es constante en cada minterm. Determinamos el valor\(s_i\) de\(X\) en cada minterm\(M_i\). Esto describe\(X\) en una forma primitiva especial
Aplicamos la operación csort a las matrices de valores y probabilidades minterm para determinar la distribución para\(X\).
Ilustramos con un ejemplo sencillo. La extensión al caso general debe ser bastante evidente. Primero, hacemos el problema “a mano” en forma tabular. Entonces utilizamos los m-procedimientos para llevar a cabo las operaciones deseadas.
Ejemplo\(\PageIndex{9}\) Finding the distribution from affine form
Una casa de pedidos por correo cuenta con tres artículos (límite de uno de cada tipo por cliente). Let
- \(E_1\)= el evento que el cliente ordena el artículo 1, a un precio de 10 dólares.
- \(E_2\)= el evento que el cliente ordena el artículo 2, a un precio de 18 dólares.
- \(E_3\)= el evento que el cliente ordena el artículo 3, a un precio de 10 dólares.
Hay un cargo por correo de 3 dólares por pedido.
Suponemos que\(\{E_1, E_2, E_3\}\) es independiente con probabilidades 0.6, 0.3, 0.5, respectivamente. \(X\)Sea la cantidad que un cliente que ordena los artículos especiales gasta en ellos más el costo de envío. Entonces, en forma afín,
\(X = 10 I_{E_1} + 18 I_{E_2} + 10 I_{E_3} + 3\)
Buscamos primero la forma primitiva, usando las probabilidades minterm, que pueden calcularse en este caso usando la función m minprob.
- Para obtener el valor de\(X\) en cada minterm
- Multiplicar el vector minterm para cada evento generador por el coeficiente para ese evento
- Suma los valores en cada minterm y suma la constante
Para completar la tabla, enumere las probabilidades minterm correspondientes.
\(i\) 10\(I_{E_1}\) 18\(I_{E_2}\) 10\(I_{E_3}\) c \(s-i\) \(pm_i\) 0 0 0 0 3 3 0.14 1 0 0 10 3 13 0.14 2 0 18 0 3 21 0.06 3 0 18 10 3 31 0.06 4 10 0 0 3 13 0.21 5 10 0 10 3 23 0.21 6 10 18 0 3 31 0.09 7 10 18 10 3 41 0.09 Entonces ordenamos en el\(s_i\), los valores en los diversos\(M_i\), para exponer más claramente la forma primitiva para\(X\).
Valores de “forma primitiva” \(i\) \(s_i\) \(pm_i\) 0 3 0.14 1 13 0.14 4 13 0.21 2 21 0.06 5 23 0.21 3 31 0.06 6 31 0.09 7 41 0.09 La forma primitiva de\(X\) es así
\ (X = 3I_ {M_0} + 12I_ {M_1} + 13I_ {M_4} + 21I_ {M_2} + 23I_ {M_5} + 31I_ {M_3} + 31I_ {M_6} + 41I_ {M_7}
Observamos que el valor 13 se toma en minterms\(M_1\) y\(M_4\). La probabilidad\(X\) tiene el valor 13 es así\(p(1) + p(4)\). De igual manera,\(X\) tiene valor 31 sobre minterms\(M_3\) y\(M_6\).
- Para completar el proceso de determinación de la distribución, enumeramos los valores ordenados y consolidamos sumando las probabilidades de los minterms sobre los que se toma cada valor, de la siguiente manera:
\(k\) \(t_k\) \(p_k\) 1 3 0.14 2 13 0.14 + 0.21 = 0.35 3 21 0.06 4 23 0.21 5 31 0.06 + 0.09 = 0.15 6 41 0.09 Los resultados se pueden poner en una matriz\(X\) de valores posibles y una matriz correspondiente PX de probabilidades que\(X\) tome cada uno de estos valores. El examen de la tabla muestra que
\(X =\)[3 13 21 23 31 41] y\(PX =\) [0.14 0.35 0.06 0.21 0.15 0.09]
Matrices\(X\) y PX describen la distribución para\(X\).
Un procedimiento m para determinar la distribución a partir de la forma afín
Ahora consideramos los pasos adecuados de MATLAB para determinar la distribución a partir de la forma afín, luego incorporarlos en el procedimiento m canónico para llevar a cabo la transformación. Comenzamos con la variable aleatoria en forma afín, y suponemos que tenemos disponibles, o podemos calcular, las probabilidades minterm.
El procedimiento utiliza mintable para establecer los patrones vectoriales básicos minterm, luego usa una matriz de coeficientes, incluyendo el término constante (establecido a cero si está ausente), para obtener los valores en cada minterm. Las probabilidades minterm se incluyen en una matriz de filas.
Habiendo obtenido los valores en cada minterm, el procedimiento realiza la consolidación deseada mediante el uso de la función m csort.
Ejemplo\(\PageIndex{10}\) Steps in determining the distribution for X in Example 6.1.9
>> c = [10 18 10 3]; % Constant term is listed last
>> pm = minprob(0.1*[6 3 5]);
>> M = mintable(3) % Minterm vector pattern
M =
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
% - - - - - - - - - - - - - - % An approach mimicking ``hand'' calculation
>> C = colcopy(c(1:3),8) % Coefficients in position
C =
10 10 10 10 10 10 10 10
18 18 18 18 18 18 18 18
10 10 10 10 10 10 10 10
>> CM = C.*M % Minterm vector values
CM =
0 0 0 0 10 10 10 10
0 0 18 18 0 0 18 18
0 10 0 10 0 10 0 10
>> cM = sum(CM) + c(4) % Values on minterms
cM =
3 13 21 31 13 23 31 41
% - - - - - - - - - - - - - % Practical MATLAB procedure
>> s = c(1:3)*M + c(4)
s =
3 13 21 31 13 23 31 41
>> pm = 0.14 0.14 0.06 0.06 0.21 0.21 0.09 0.09 % Extra zeros deleted
>> const = c(4)*ones(1,8);}
>> disp([CM;const;s;pm]') % Display of primitive form
0 0 0 3 3 0.14 % MATLAB gives four decimals
0 0 10 3 13 0.14
0 18 0 3 21 0.06
0 18 10 3 31 0.06
10 0 0 3 13 0.21
10 0 10 3 23 0.21
10 18 0 3 31 0.09
10 18 10 3 41 0.09
>> [X,PX] = csort(s,pm); % Sorting on s, consolidation of pm
>> disp([X;PX]') % Display of final result
3 0.14
13 0.35
21 0.06
23 0.21
31 0.15
41 0.09
Los dos pasos básicos se combinan en el procedimiento m canónico, que utilizamos para resolver el problema anterior.
Ejemplo\(\PageIndex{11}\) Use of canonic on the variables of Example 6.1.10
>> c = [10 18 10 3]; % Note that the constant term 3 must be included last
>> pm = minprob([0.6 0.3 0.5]);
>> canonic
Enter row vector of coefficients c
Enter row vector of minterm probabilities pm
Use row matrices X and PX for calculations
Call for XDBN to view the distribution
>> disp(XDBN)
3.0000 0.1400
13.0000 0.3500
21.0000 0.0600
23.0000 0.2100
31.0000 0.1500
41.0000 0.0900
Con la distribución disponible en las matrices\(X\) (conjunto de valores) y PX (conjunto de probabilidades), podemos calcular una amplia variedad de cantidades asociadas a la variable aleatoria.
Utilizamos dos dispositivos clave:
- Utilice operaciones relacionales y lógicas en la matriz de valores\(X\) para determinar una matriz\(M\) que tenga unas para aquellos valores que cumplan una condición prescrita. \(P(X \in M)\): PM = M*PX'
- Determine\(G = g(X) = [g(X_1) g(X_2) \cdot\cdot\cdot g(X_n)]\) mediante el uso de operaciones de matriz en matriz\(X\). Tenemos dos alternativas:
- Utilice la matriz\(G\), que tiene valores\(g(t_i)\) para cada valor posible\(t_i\) para\(X\), o,
- Aplicar csort al par\((G, PX)\) para obtener la distribución para\(Z = g(X)\). Esta distribución (en matrices de valor y probabilidad) puede ser utilizada exactamente de la misma manera que para la variable aleatoria original\(X\).
Ejemplo\(\PageIndex{12}\) Continuation of Example 6.1.11
Supongamos que para la variable aleatoria\(X\) en el Ejemplo 6.11 se desea determinar las probabilidades
\(P(15 \le X \le 35)\),\(P(|X - 20| \le 7)\), y\((X - 10) (X - 25) > 0)\)
>> M = (X>=15)&(X<=35); M = 0 0 1 1 1 0 % Ones for minterms on which 15 <= X <= 35 >> PM = M*PX' % Picks out and sums those minterm probs PM = 0.4200 >> N = abs(X-20)<=7; N = 0 1 1 1 0 0 % Ones for minterms on which |X - 20| <= 7 >> PN = N*PX' % Picks out and sums those minterm probs PN = 0.6200 >> G = (X - 10).*(X - 25) G = 154 -36 -44 -26 126 496 % Value of g(t_i) for each possible value >> P1 = (G>0)*PX' % Total probability for those t_i such that P1 = 0.3800 % g(t_i) > 0 >> [Z,PZ] = csort(G,PX) % Distribution for Z = g(X) Z = -44 -36 -26 126 154 496 PZ = 0.0600 0.3500 0.2100 0.1500 0.1400 0.0900 >> P2 = (Z>0)*PZ' % Calculation using distribution for Z P2 = 0.3800
Ejemplo\(\PageIndex{13}\) Alternate formulation of Example 4.3.3 from "Composite Trials"
Diez autos de carreras participan en contrarreloj para determinar las pole positions para una próxima carrera. Para calificar, deben publicar una velocidad promedio de 125 mph o más en una carrera de prueba. Que\(E_i\) sea el evento el auto\(i\) th hace velocidad clasificatoria. Parece razonable suponer que la clase\(\{E_i: 1 \le i \le 10\}\) es independiente. Si las probabilidades de éxito respectivas son 0.90, 0.88, 0.93, 0.77, 0.85, 0.96, 0.72, 0.83, 0.91, 0.84, ¿cuál es la probabilidad de que\(k\) o más califiquen (\(k\)= 6,7,8,9,10)?
Solución
Let\(X = \sum_{i = 1}^{10} I_{E_i}\)
>> c = [ones(1,10) 0];
>> P = [0.90, 0.88, 0.93, 0.77, 0.85, 0.96, 0.72, 0.83, 0.91, 0.84];
>> canonic
Enter row vector of coefficients c
Enter row vector of minterm probabilities minprob(P)
Use row matrices X and PX for calculations
Call for XDBN to view the distribution
>> k = 6:10;
>> for i = 1:length(k)
Pk(i) = (X>=k(i))*PX';
end
>> disp(Pk)
0.9938 0.9628 0.8472 0.5756 0.2114
Esta solución no es tan conveniente de escribir. Sin embargo, con la distribución para\(X\) como se define, se pueden determinar muchas otras probabilidades. Esto es particularmente el caso cuando se desea comparar los resultados de dos carreras independientes o “heats”. Consideramos tales problemas en el estudio de Clases Independientes de Variables Aleatorias.
Una forma de función para canónico
Una desventaja del procedimiento canónico es que siempre nombra la salida\(X\) y PX. Si bien estos pueden renombrarse fácilmente, frecuentemente es deseable usar algún otro nombre para la variable aleatoria desde el principio. Una forma de función, que llamamos canonicf, es útil en este caso.
Ejemplo\(\PageIndex{14}\) Alternate solution of Example 6.1.13, using canonicf
>> c = [10 18 10 3];
>> pm = minprob(0.1*[6 3 5]);
>> [Z,PZ] = canonicf(c,pm);
>> disp([Z;PZ]') % Numbers as before, but the distribution
3.0000 0.1400 % matrices are now named Z and PZ
13.0000 0.3500
21.0000 0.0600
23.0000 0.2100
31.0000 0.1500
41.0000 0.0900
Variables aleatorias generales
La distribución para una variable aleatoria simple se visualiza fácilmente como concentraciones de masa puntual en los diversos valores del rango, y la clase de eventos determinada por una variable aleatoria simple se describe en términos de la partición generada por\(X\) (es decir, la clase de esos eventos de la forma \(A_i = [X = t_i]\)para cada uno\(t_i\) en el rango). La situación es conceptualmente la misma para el caso general, pero los detalles son más complicados. Si la variable aleatoria toma un continuo de valores, entonces la distribución de la masa de probabilidad se puede extender suavemente en la línea. O bien, la distribución puede ser una mezcla de concentraciones de masa puntual y distribuciones suaves en algunos intervalos. La clase de eventos determinada por\(X\) es el conjunto de todas las imágenes inversas\(X^{-1} (M)\) para\(M\) cualquier miembro de una clase general de subconjuntos de subconjuntos de la línea real conocida en la literatura matemática como los conjuntos de Borel. Hay razones técnicas matemáticas para no decir que M es un subconjunto, pero la clase de conjuntos de Borel es lo suficientemente general como para incluir cualquier conjunto que pueda encontrarse en las aplicaciones, ciertamente al nivel de este tratamiento. Los conjuntos de Borel incluyen cualquier intervalo y cualquier conjunto que pueda estar formado por complementos, uniones contables e intersecciones contables de conjuntos de Borel. Este es un tipo de clase conocida como álgebra sigma de eventos. Debido a la preservación de las operaciones de conjunto por la imagen inversa, la clase de eventos determinada por la variable aleatoria también\(X\) es un álgebra sigma, y a menudo se designa\(\sigma(X)\). Existen algunas preguntas técnicas sobre la medida de probabilidad\(P_X\) inducida por\(X\), de ahí la distribución. Estos también se resuelven de tal manera que no hay necesidad de preocupación en este nivel de análisis. Sin embargo, algunas de estas preguntas adquieren importancia para tratar procesos aleatorios y otras nociones avanzadas cada vez más utilizadas en aplicaciones. Dos hechos proporcionan la libertad que necesitamos para proceder con poca preocupación por los detalles técnicos.
\(X^{-1} (M)\)es un evento para cada Borel set\(M\) iff para cada intervalo semi-infinito\((-\infty, t]\) en la línea real\(X^{-1} ((-\infty, t])\) es un evento.
La distribución de probabilidad inducida se determina únicamente por su asignación a todos los intervalos de la forma\((-\infty, t]\).
Estos hechos apuntan a la importancia de la función de distribución introducida en el siguiente capítulo.
Otro hecho, aludido anteriormente y discutido con cierto detalle en el siguiente capítulo, es que cualquier variable aleatoria general puede aproximarse tan estrechamente como complacida por una simple variable aleatoria. Pasamos en el siguiente capítulo a una descripción de ciertas distribuciones de probabilidad comúnmente encontradas y formas de describirlas analíticamente.


