Caso C-C

CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.

Objetivos de aprendizaje

LO 4.20: Clasificar una situación de análisis de datos que involucra dos variables según la “clasificación de tipo rol”.

Objetivos de aprendizaje

LO 4.21: Para una situación de análisis de datos que involucre dos variables, determinar la (s) visualización (es) gráfica (es) apropiada (s) y/o medidas numéricas que deben usarse para resumir los datos.

Video

Vídeo: Caso C-C (10:34)

Tutoriales SAS relacionados

• 6A — (3:07) Mesas Bidireccionales (Contingencia) — EDA

Tutoriales relacionados con SPSS

• 6A — (7:57) Mesas Bidireccionales (Contingencia) — EDA

Dos variables categóricas

Recordemos la tabla de clasificación de tipo rol para enmarcar nuestra discusión sobre la relación entre dos variables:

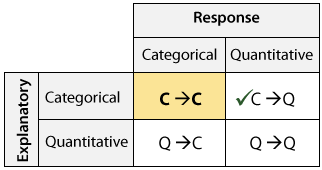
Terminamos con el caso C→Q, y ahora pasaremos al caso C→C, donde examinamos la relación entre dos variables categóricas.

Anteriormente en el curso, (cuando discutimos la distribución de una sola variable categórica) examinamos los datos obtenidos cuando se preguntó a una muestra aleatoria de 1,200 estudiantes universitarios estadounidenses sobre su imagen corporal (bajo peso, sobrepeso o sobre la derecha). Ahora volvemos a este ejemplo, para abordar la siguiente pregunta:

Si hubiéramos separado nuestra muestra de 1,200 estudiantes universitarios estadounidenses por género y hubiéramos visto a hombres y mujeres por separado, ¿habríamos encontrado una distribución similar entre las categorías de imagen corporal? Más específicamente, ¿son los hombres y las mujeres igual de propensos a pensar que su peso es correcto? Entre esos estudiantes que no piensan que su peso es lo correcto, ¿hay alguna diferencia entre los géneros en los sentimientos sobre la imagen corporal?

Responder a estas preguntas requiere examinar la relación entre dos variables categóricas, género e imagen corporal. Porque la cuestión de interés es si existe un efecto de género en la imagen corporal,

• la variable explicativa es género, y
• la variable de respuesta es imagen corporal.

Así es como se ven los datos brutos cuando incluimos el género de cada alumno:

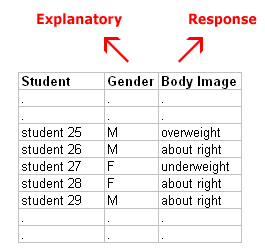
Una vez más los datos brutos son una larga lista de 1,200 géneros y respuestas, y por lo tanto no son muy útiles en esa forma.

Tablas de Contingencia

Objetivos de aprendizaje

LO 4.22: Definir y explicar el proceso de creación de una tabla de contingencia (tabla bidireccional).

Para iniciar nuestra exploración de cómo se relaciona la imagen corporal con el género, necesitamos una exhibición informativa que resuma los datos. Para resumir la relación entre dos variables categóricas, creamos una pantalla llamada tabla bidireccional o tabla de contingencia.

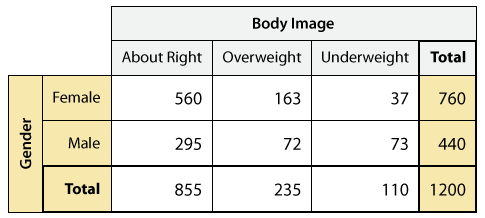
Aquí está la mesa bidireccional para nuestro ejemplo:

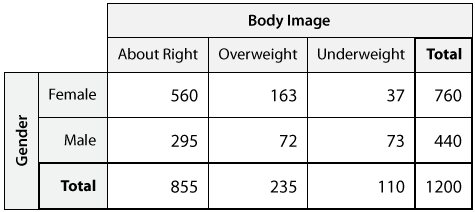
La tabla tiene los géneros posibles en las filas, y las posibles respuestas con respecto a la imagen corporal en las columnas. En cada intersección entre fila y columna, colocamos los recuentos de cuántas veces esa combinación de género e imagen corporal ocurrió en los datos. Sumamos a través de las filas para rellenar la columna Total, y sumamos a través de las columnas para rellenar la fila Total.

Completar las siguientes actividades relacionadas con estos datos.

Aprender haciendo: Caso C-C

Comentarios:

Tenga en cuenta que a partir de la forma en que se construye la tabla bidireccional, la fila o columna Total es un resumen de una de las dos variables categóricas, ignorando la otra. En nuestro ejemplo:

• La fila Total da el resumen de la imagen corporal de la variable categórica:

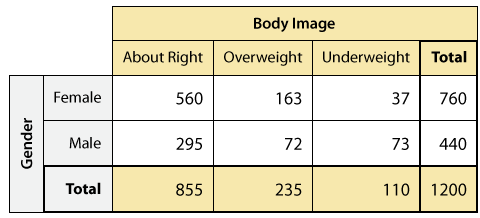
• La columna Total da el resumen de la variable categórica género: (Estos son los mismos recuentos que encontramos anteriormente en el curso cuando miramos la imagen corporal de la variable categórica única, y no consideramos género).

Búsqueda de porcentajes condicionales (fila y columna)

Objetivos de aprendizaje

LO 4.23: Dada una tabla de contingencia (tabla bidireccional), interpretar la información que revela sobre la asociación entre dos variables categóricas calculando y comparando porcentajes condicionales.

Hasta ahora hemos organizado los datos brutos en una pantalla mucho más informativa, la tabla bidireccional:

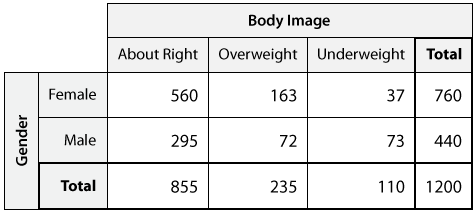
Recuerde, sin embargo, que nuestro objetivo principal es explorar cómo la imagen corporal se relaciona con el género. Explorar la relación entre dos variables categóricas (en este caso imagen corporal y género) equivale a comparar las distribuciones de la variable respuesta (en este caso imagen corporal) a través de los diferentes valores de la variable explicativa (en este caso hombres y mujeres):

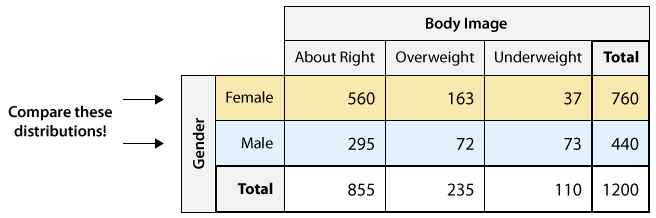
Tenga en cuenta que no tiene sentido comparar los recuentos crudos, porque en general hay más hembras que machos. Entonces, por ejemplo, no es muy informativo decir “hay 560 hembras que respondieron 'sobre la correcta' en comparación con sólo 295 machos”, ya que las 560 hembras son de un total de 760, y los 295 machos son de un total de sólo 440.

Necesitamos complementar nuestra pantalla, la mesa bidireccional, con algunas medidas numéricas que nos permitan comparar las distribuciones. Estas medidas numéricas se encuentran simplemente convirtiendo los recuentos a porcentajes dentro (o restringidos a) cada valor de la variable explicativa por separado.

En nuestro ejemplo: Miramos cada género por separado, y convertimos los recuentos a porcentajes dentro de ese género. Empecemos con las hembras:

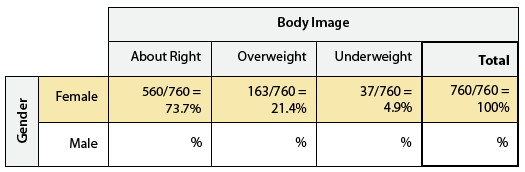
Obsérvese que cada conteo se convierte en porcentajes dividiendo por el número total de hembras, 760. Estas medidas numéricas se denominan porcentajes condicionales, ya que las encontramos por “condicionamiento” en uno de los géneros.

Ahora completa las siguientes actividades para calcular los porcentajes de fila para machos.

Aprender haciendo: Cálculo de porcentajes de fila

Comentarios:

• En nuestro ejemplo, optamos por organizar los datos con la variable explicativa género en filas y la variable de respuesta imagen corporal en columnas, y así nuestros porcentajes condicionales fueron porcentajes de fila, calculados dentro de cada fila por separado. De igual manera, si la variable explicativa pasa a sentarse en columnas y la variable de respuesta en filas, nuestros porcentajes condicionales serán porcentajes de columna, calculados dentro de cada columna por separado. Para un ejemplo, vea el “¿Conseguí esto?” ejercicios a continuación.

• Otra forma de visualizar los porcentajes condicionales, en lugar de una tabla, es el gráfico de barras dobles. Esta exhibición es bastante común en los periódicos.

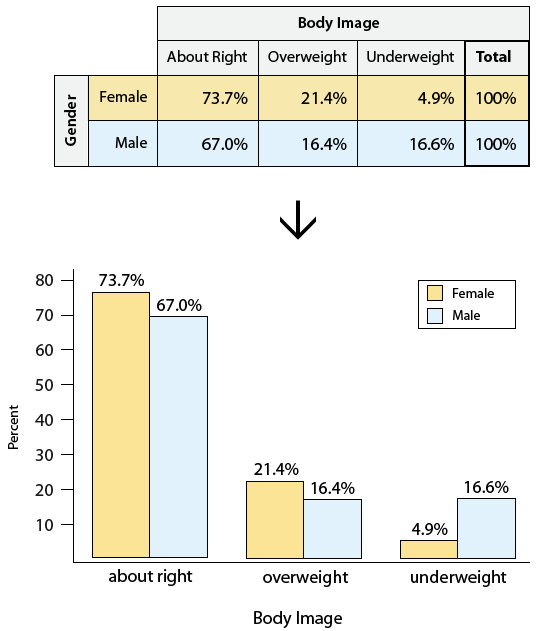
Ahora que hemos resumido la relación entre las variables categóricas género e imagen corporal, volvamos e interpretemos los resultados en el contexto de las preguntas que planteamos.

Aprender haciendo: Interpretación en el Caso C-C

Aprende haciendo: Case C-C (Software)

Para la práctica adicional complete las siguientes actividades.

¿Conseguí esto? : Caso C-C

Vamos a resumir

• La relación entre dos variables categóricas se resume utilizando:
  • Visualización de datos: mesa bidireccional, complementada por
  • Medidas numéricas: porcentajes condicionales.
• Los porcentajes condicionales se calculan por separado para cada valor de la variable explicativa. Pueden ser porcentajes de fila, si la variable explicativa “se sienta” en las filas, o porcentajes de columna, si la variable explicativa “se sienta” en las columnas.
• Cuando tratamos de entender la relación entre dos variables categóricas, comparamos las distribuciones de la variable de respuesta para los valores de la variable explicativa. En particular, observamos cómo el patrón de porcentajes condicionales difiere entre los valores de la variable explicativa.