Caso Q-Q
- Última actualización
- Guardar como PDF
- Page ID
- 151254
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.20: Clasificar una situación de análisis de datos que involucra dos variables de acuerdo con la “clasificación de tipo rol”.
Objetivos de aprendizaje
LO 4.21: Para una situación de análisis de datos que involucre dos variables, determinar la (s) visualización (es) gráfica (es) apropiada (s) y/o medidas numéricas que deben usarse para resumir los datos.
Video
Vídeo: Caso Q-Q (2:30)
Tutoriales SAS relacionados
- 9A — (3:53) Gráfica de dispersión básica
- 9B — (2:29) Gráfica de dispersión agrupada
- 9C — (3:46) Coeficiente de correlación de Pearson
- 9D — (3:00) Regresión lineal simple — EDA
Tutoriales relacionados con SPSS
- 9A — (2:38) Gráfica de dispersión básica
- 9B — (2:54) Gráfica de dispersión agrupada
- 9C — (3:35) Coeficiente de correlación de Pearson
- 9D — (2:53) Regresión lineal simple — EDA
Introducción — Dos Variables Cuantitativas
Aquí nuevamente está la tabla de clasificación de tipo rol para enmarcar nuestra discusión sobre la relación entre dos variables:
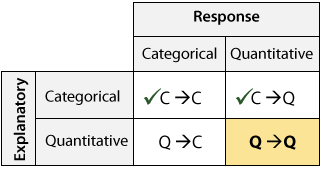
Antes de seguir leyendo, pruebe este applet interactivo de análisis de datos en línea.
Applet Interactivo: Case Q-Q
Terminamos con los casos C→Q y C→C, y ahora pasaremos al caso Q→Q, donde examinaremos la relación entre dos variables cuantitativas.
En esta sección discutiremos diagramas de dispersión, que son la visualización visual adecuada en este caso junto con métodos numéricos para relaciones lineales incluyendo correlación y regresión lineal.
Diagramas de dispersión
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.21: Para una situación de análisis de datos que involucre dos variables, determinar la (s) visualización (es) gráfica (es) apropiada (s) y/o medidas numéricas que deben usarse para resumir los datos.
Video
Video: Gráficas de dispersión (7:20)
Tutoriales SAS relacionados
- 9A — (3:53) Gráfica de dispersión básica
- 9B — (2:29) Gráfica de dispersión agrupada
- 9C — (3:46) Coeficiente de correlación de Pearson
- 9D — (3:00) Regresión lineal simple — EDA
Tutoriales relacionados con SPSS
- 9A — (2:38) Gráfica de dispersión básica
- 9B — (2:54) Gráfica de dispersión agrupada
- 9C — (3:35) Coeficiente de correlación de Pearson
- 9D — (2:53) Regresión lineal simple — EDA
En los dos casos anteriores tuvimos una variable explicativa categórica, por lo que se exploró la relación entre las dos variables comparando la distribución de la variable respuesta para cada categoría de la variable explicativa:
- En el caso C→Q comparamos distribuciones de la respuesta cuantitativa.
- En el caso C→C comparamos distribuciones de la respuesta categórica.
El caso Q→Q es diferente en el sentido de que ambas variables (en particular la variable explicativa) son cuantitativas. Como descubrirás, aunque todavía estamos en esencia comparando la distribución de una variable para diferentes valores de la otra, este caso requerirá de un tipo diferente de tratamiento y herramientas.
Objetivos de aprendizaje
LO 4.24: Explicar el proceso de creación de una gráfica de dispersión.
Creación de diagramas de dispersión
Empecemos con un ejemplo:
EJEMPLO: Señales viales
Una firma de investigación de Pensilvania realizó un estudio en el que se muestrearon 30 conductores (de 18 a 82 años de edad), y para cada uno se determinó la distancia máxima (en pies) a la que pudo leer un letrero de nuevo diseño. El objetivo de este estudio fue explorar la relación entre la edad del conductor y la distancia máxima a la que los signos eran legibles, y luego utilizar los hallazgos del estudio para mejorar la seguridad de los conductores mayores. (Referencia: Utts y Heckard, Mind on Statistics (2002). Fuente original: Datos recopilados por Last Resource, Inc, Bellfonte, PA.)
Dado que el propósito de este estudio es explorar el efecto de la edad en la distancia máxima de legibilidad,
- la variable explicativa es Edad, y
- la variable de respuesta es Distancia.
Así es como se ven los datos sin procesar:
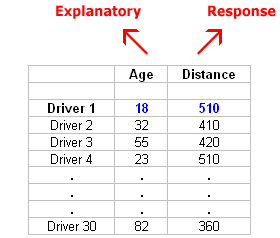
Tenga en cuenta que la estructura de datos es tal que para cada individuo (en este caso conductor 1... conductor 30) tenemos un par de valores (en este caso que representa la edad y distancia del conductor). Por lo tanto, podemos pensar en estos datos como 30 pares de valores: (18, 510), (32, 410), (55, 420),..., (82, 360).
El primer paso para explorar la relación entre la edad del conductor y la distancia de legibilidad de los signos es crear una visualización gráfica adecuada e informativa. La representación gráfica adecuada para examinar la relación entre dos variables cuantitativas es la gráfica de dispersión. Así es como se construye una gráfica de dispersión para nuestro ejemplo:
Para crear una gráfica de dispersión, se traza cada par de valores, de manera que el valor de la variable explicativa (X) se traza en el eje horizontal, y el valor de la variable de respuesta (Y) se traza en el eje vertical. En otras palabras, cada individuo (driver, en nuestro ejemplo) aparece en la gráfica de dispersión como un punto único cuya coordenada X es el valor de la variable explicativa para ese individuo, y cuya coordenada Y es el valor de la variable de respuesta. Aquí hay una ilustración:
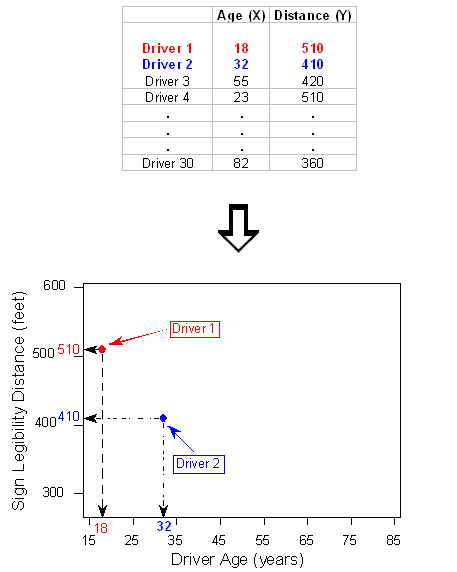
Y aquí está la trama de dispersión terminada:
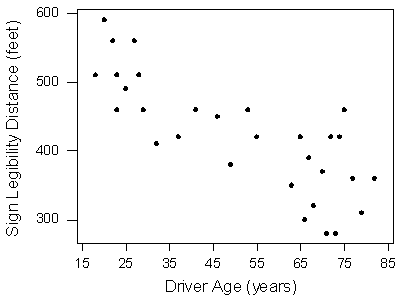
Comentario:
- Es importante mencionar nuevamente que al crear una gráfica de dispersión, la variable explicativa siempre se debe trazar en el eje X horizontal, y la variable de respuesta se debe trazar en el eje Y vertical. Si en un ejemplo específico no tenemos una distinción clara entre variables explicativas y de respuesta, cada una de las variables se puede trazar en cualquiera de los ejes.
Interpretación de diagramas de dispersión
Objetivos de aprendizaje
LO 4.25: Describir la relación mostrada en una gráfica de dispersión incluyendo: a) el patrón general, b) desviaciones llamativas del patrón.
¿Cómo exploramos la relación entre dos variables cuantitativas usando la gráfica de dispersión? ¿A qué debemos mirar o prestar atención?
Recordemos que cuando describimos la distribución de una sola variable cuantitativa con un histograma, describimos el patrón general de la distribución (forma, centro, propagación) y cualquier desviación de ese patrón (valores atípicos). Hacemos lo mismo con la trama de dispersión. La siguiente figura resume este punto:
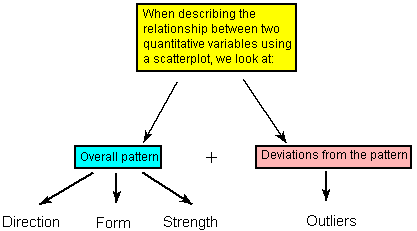
Como explica la figura, al describir el patrón general de la relación observamos su dirección, forma y fuerza.
Dirección
- La dirección de la relación puede ser positiva, negativa, o ninguna:
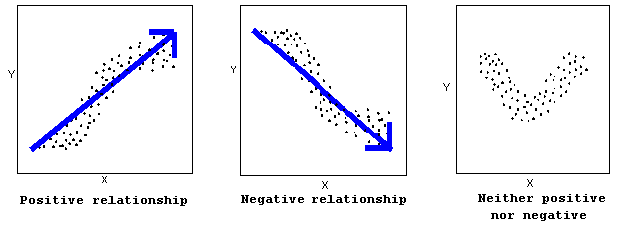
Una relación positiva (o creciente) significa que un aumento en una de las variables se asocia con un aumento en la otra.
Una relación negativa (o decreciente) significa que un aumento en una de las variables se asocia con una disminución en la otra.
No todas las relaciones pueden clasificarse como positivas o negativas.
Formulario
- La forma de la relación es su forma general. Al identificar la forma, tratamos de encontrar la forma más sencilla de describir la forma de la gráfica de dispersión. Hay muchas formas posibles. Aquí hay una pareja que son bastante comunes:
Las relaciones con una forma lineal se describen más simplemente como puntos dispersos alrededor de una línea:
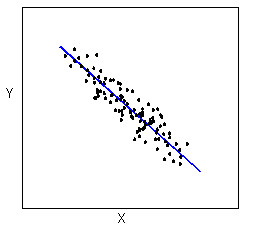
Las relaciones con una forma no lineal (a veces llamada curvilínea) se describen más simplemente como puntos dispersos alrededor de la misma línea curva:
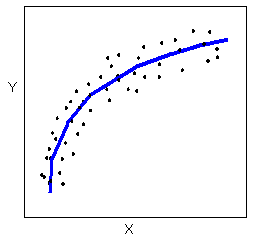
Existen muchas otras formas posibles para la relación entre dos variables cuantitativas, pero las formas lineales y curvilíneas son bastante comunes y fáciles de identificar. Otro patrón relacionado con el formulario que debemos tener en cuenta son los clústeres en los datos:
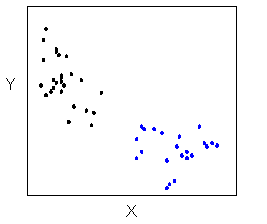
Fuerza
- La fuerza de la relación está determinada por la cercanía con la que los datos siguen la forma de la relación. Veamos, por ejemplo, los dos diagramas de dispersión siguientes que muestran relaciones lineales positivas:
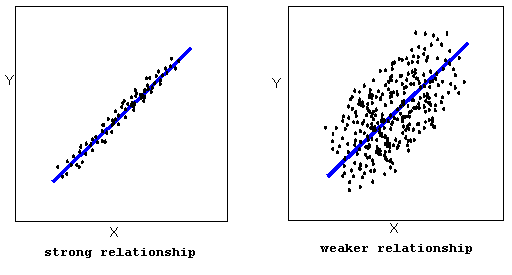
La fuerza de la relación está determinada por la cercanía con la que los puntos de datos siguen la forma. Podemos ver que en la gráfica de dispersión izquierda los puntos de datos siguen bastante de cerca el patrón lineal. Este es un ejemplo de una relación fuerte. En la gráfica de dispersión derecha, los puntos también siguen el patrón lineal, pero mucho menos de cerca, y por lo tanto podemos decir que la relación es más débil. En general, sin embargo, evaluar la fuerza de una relación con solo mirar la trama de dispersión es bastante problemático, y necesitamos una medida numérica que nos ayude con eso. Lo discutiremos más adelante en esta sección.
- Los puntos de datos que se desvían del patrón de la relación se denominan valores atípicos. Veremos varios ejemplos de valores atípicos durante esta sección. Dos valores atípicos se ilustran en la gráfica de dispersión a continuación:
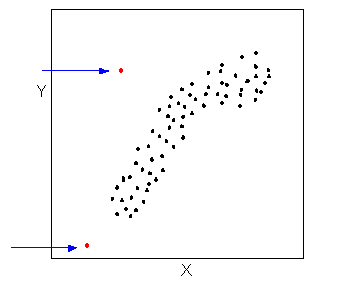
Volvamos ahora a nuestro ejemplo, y utilicemos la gráfica de dispersión para examinar la relación entre la edad del conductor y la distancia máxima de legibilidad de señal.
EJEMPLO: Señales viales
Aquí está la gráfica de dispersión:
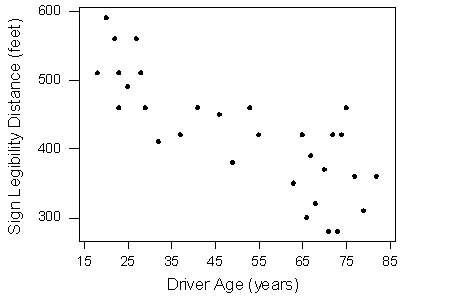
El rumbo de la relación es negativo, lo cual tiene sentido en el contexto, ya que a medida que envejece tu vista se debilita, y en particular los conductores mayores tienden a poder leer señales solo a distancias menores. Una flecha dibujada sobre la gráfica de dispersión ilustra la dirección negativa de esta relación:
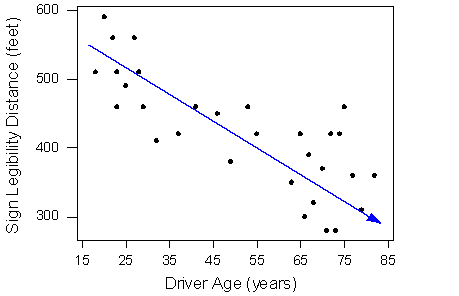
La forma de la relación parece ser lineal. Observe cómo los puntos tienden a estar dispersos por la línea. Si bien, como mencionamos anteriormente, es problemático evaluar la fuerza sin una medida numérica, la relación parece ser moderadamente fuerte, ya que los datos están bastante dispersos alrededor de la línea. Por último, todos los puntos de datos parecen “obedecer” al patrón —no parece haber ningún valor atípico.
Ahora veremos dos ejemplos más:
EJEMPLO: Período promedio de gestación
El período promedio de gestación, o tiempo de embarazo, de un animal está estrechamente relacionado con su longevidad (la duración de su vida). Se han examinado datos sobre el período promedio de gestación y longevidad (en cautiverio) de 40 especies diferentes de animales, con el propósito de examinar cómo se relaciona el período de gestación de un animal con (o puede predecirse a partir de) su longevidad. (Fuente: Rossman y Chance. (2001). Estadísticas del taller: Descubrimiento con datos y Minitab. Fuente original: El almanaque mundial de 1993 y libro de hechos).
Aquí está la gráfica de dispersión de los datos.
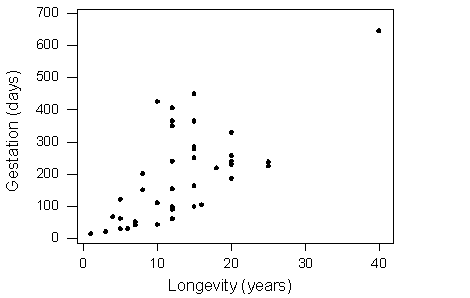
¿Qué podemos aprender de la relación a partir de la trama de dispersión? La dirección de la relación es positiva, lo que significa que los animales con mayores períodos de vida tienden a tener tiempos de embarazo más largos (esto tiene sentido intuitivo). Una flecha dibujada sobre la gráfica de dispersión a continuación ilustra esto:
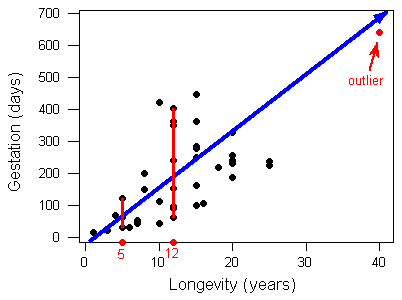
La forma de la relación vuelve a ser esencialmente lineal. Parece haber un valor atípico, lo que indica un animal con una longevidad y un período de gestación excepcionalmente largos. (Este animal pasa a ser el elefante.) Tenga en cuenta que si bien este valor atípico definitivamente se desvía del resto de los datos en términos de su magnitud, sí sigue la dirección de los datos.
Comentario:
- Otra característica de la gráfica de dispersión que vale la pena observar es cómo la variación en la gestación aumenta a medida que aumenta la longevidad. Este hecho es ilustrado por las dos líneas verticales rojas en la parte inferior izquierda de la gráfica. Tenga en cuenta que los periodos de gestación para los animales que viven 5 años van desde aproximadamente 30 días hasta aproximadamente 120 días. Por otro lado, los periodos de gestación de los animales que viven 12 años varían mucho más, y van desde alrededor de 60 días hasta más de 400 días.
Ejemplo: Uso de combustible
Como tercer ejemplo, considere la relación entre la cantidad promedio de combustible utilizada (en litros) para conducir una distancia fija en un automóvil (100 kilómetros), y la velocidad a la que se conduce el automóvil (en kilómetros por hora). (Fuente: Moore y McCabe, (2003). Introducción a la práctica de la estadística. Fuente original: T.N. Lam. (1985). “Estimación del consumo de combustible para el tamaño del motor”, Journal of Transportation Engineering, vol. 111)
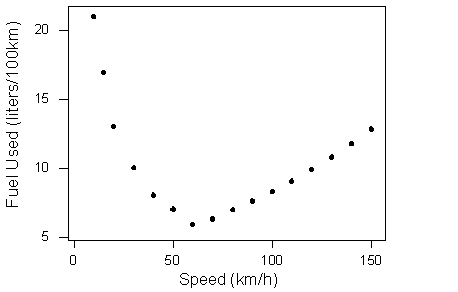
Los datos describen una relación que disminuye y luego aumenta — la cantidad de combustible consumido disminuye rápidamente a un mínimo para un automóvil que conduce 60 kilómetros por hora, y luego aumenta gradualmente para velocidades superiores a 60 kilómetros por hora. Esto sugiere que la velocidad a la que un automóvil economiza más en combustible es de unos 60 km/h, lo que forma una relación no lineal (curvilínea) que parece ser muy fuerte, ya que las observaciones parecen encajar perfectamente en la curva. Por último, no parece haber ningún valor atípico.
Aprender haciendo: Scatterplots
EJEMPLO: Retorno de incentivos
El ejemplo en la última actividad brinda una gran oportunidad para la interpretación de la forma de la relación en contexto. Recordemos que el ejemplo examinó cómo el porcentaje de participantes que completaron una encuesta se ve afectado por el incentivo monetario que los investigadores prometieron a los participantes. Aquí de nuevo está la gráfica de dispersión que muestra la relación:
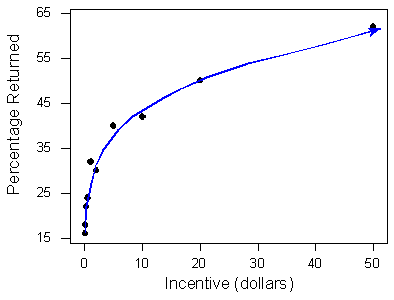
La relación positiva definitivamente tiene sentido en contexto, pero ¿cuál es la interpretación de la forma no lineal (curvilínea) en el contexto del problema? ¿Cómo podemos explicar (en contexto) el hecho de que la relación parece al principio estar aumentando muy rápidamente, pero luego se ralentiza? La siguiente gráfica nos ayudará:
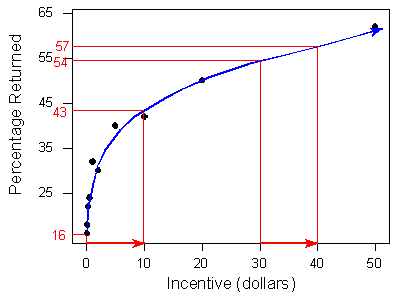
Tenga en cuenta que cuando el incentivo monetario aumenta de $0 a $10, el porcentaje de encuestas devueltas aumenta bruscamente —un incremento de 27% (de 16% a 43%). Sin embargo, el mismo incremento de $10 de $30 a $40 no da como resultado el mismo incremento dramático en el porcentaje de encuestas devueltas — da como resultado un incremento de solo 3% (de 54% a 57%). El formulario muestra el fenómeno de “rendimientos decrecientes” —una tasa de retorno que después de cierto punto no logra aumentar proporcionalmente a los desembolsos adicionales de inversión. $10 vale más para las personas en relación con $0 que $30 es relativo a $10.
Una gráfica de dispersión etiquetada (o agrupada)
En ciertas circunstancias, puede ser razonable indicar diferentes subgrupos o categorías dentro de los datos de la gráfica de dispersión, etiquetando cada subgrupo de manera diferente. El resultado a veces se denomina diagrama de dispersión etiquetado o diagrama de dispersión agrupado, y puede proporcionar más información sobre la relación que estamos explorando. Aquí hay un ejemplo.
EJEMPLO: Perros calientes
El diagrama de dispersión a continuación muestra la relación entre el contenido de sodio y calorías de 54 marcas de hot dogs. Obsérvese que en este ejemplo no existe una distinción clara explicativa-respuesta, y decidimos tener el contenido de sodio como la variable explicativa, y el contenido calórico como la variable de respuesta.
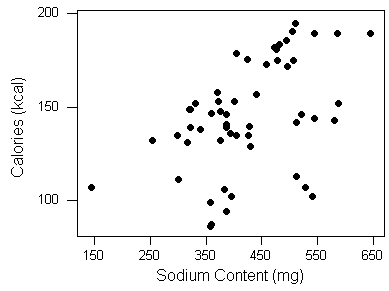
El diagrama de dispersión muestra una relación positiva, lo que significa que los hot dogs que contienen más sodio tienden a ser más altos en calorías.
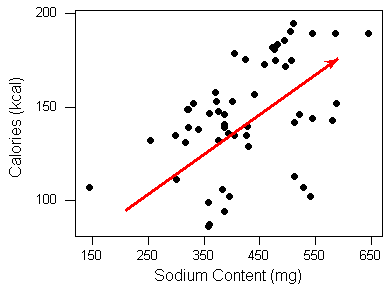
La forma de la relación, sin embargo, es algo difícil de determinar. A lo mejor si etiquetamos el diagrama de dispersión, indicando el tipo de hot dogs, obtendremos una mejor comprensión de la forma.
Aquí está la gráfica de dispersión etiquetada, con los tres colores diferentes que representan los tres tipos de hot dogs, como se indica.
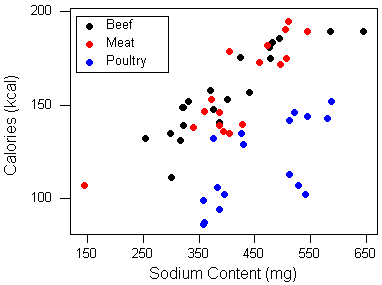
La exhibición nos da más información sobre la forma de la relación entre el sodio y el contenido calórico.
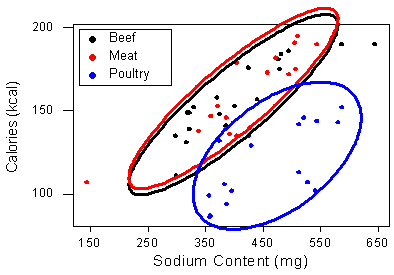
Parece que existe una relación positiva dentro de los tres tipos. En otras palabras, generalmente podemos esperar que los hot dogs que son más altos en sodio sean más altos en calorías, sin importar qué tipo de hot dog consideremos. Además, podemos ver que los hot dogs hechos de aves de corral (indicados en azul) son generalmente más bajos en calorías. Este es un resultado que hemos visto antes.
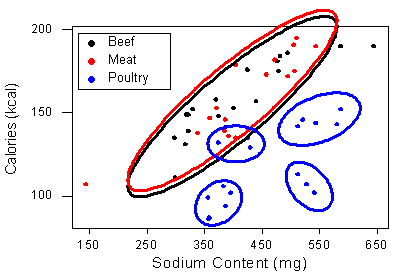
Curiosamente, parece que la forma de la relación específicamente para aves de corral se agrupa aún más, y solo podemos especular sobre si existe otra variable categórica que describa estas aparentes subcategorías de perritos calientes de aves de corral.
Aprender haciendo: Scatterplots (Software)
Resumimos
- La relación entre dos variables cuantitativas se muestra visualmente utilizando la gráfica de dispersión, donde cada punto representa a un individuo. Siempre trazamos la variable explicativa en el eje X horizontal, y la variable de respuesta en el eje Y vertical.
- Cuando exploramos una relación usando la gráfica de dispersión, debemos describir el patrón general de la relación y cualquier desviación de ese patrón. Para describir el patrón general considere la dirección, la forma y la fuerza de la relación. Evaluar la fuerza con solo mirar la gráfica de dispersión puede ser problemático; el uso de una medida numérica para determinar la fuerza se discutirá más adelante en este curso.
- Agregar etiquetas a la gráfica de dispersión que indiquen diferentes grupos o categorías dentro de los datos podría ayudarnos a obtener más información sobre la relación que estamos explorando.
Relaciones Lineales — Correlación
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.21: Para una situación de análisis de datos que involucre dos variables, determinar la (s) visualización (es) gráfica (es) apropiada (s) y/o medidas numéricas que deben usarse para resumir los datos.
Video
Vídeo: Relaciones Lineales — Correlación (8:37)
Tutoriales SAS relacionados
- 9A — (3:53) Gráfica de dispersión básica
- 9B — (2:29) Gráfica de dispersión agrupada
- 9C — (3:46) Coeficiente de correlación de Pearson
- 9D — (3:00) Regresión lineal simple — EDA
Tutoriales relacionados con SPSS
- 9A — (2:38) Gráfica de dispersión básica
- 9B — (2:54) Gráfica de dispersión agrupada
- 9C — (3:35) Coeficiente de correlación de Pearson
- 9D — (2:53) Regresión lineal simple — EDA
Introducción
Hasta ahora hemos visualizado las relaciones entre dos variables cuantitativas usando diagramas de dispersión, y descrito el patrón general de una relación considerando su dirección, forma y fuerza. Señalamos que evaluar la fuerza de una relación con solo mirar la gráfica de dispersión es bastante difícil, por lo que necesitamos complementar la gráfica de dispersión con algún tipo de medida numérica que nos ayude a evaluar la fuerza.
En esta parte, limitaremos nuestra atención al caso especial de las relaciones que tienen una forma lineal, ya que son bastante comunes y relativamente sencillas de detectar. Más importante aún, existe una medida numérica que evalúa la fuerza de la relación lineal entre dos variables cuantitativas con las que podemos complementar la gráfica de dispersión. Presentaremos aquí esta medida numérica y la discutiremos en detalle.
Aunque a partir de este punto nos vamos a centrar únicamente en las relaciones lineales, es importante recordar que no toda relación entre dos variables cuantitativas tiene una forma lineal. De hecho, hemos visto varios ejemplos de relaciones que no son lineales. Las herramientas estadísticas que aquí se introducirán son apropiadas únicamente para examinar las relaciones lineales, y como veremos, cuando se utilicen en situaciones no lineales, estas herramientas pueden generar errores en el razonamiento.
Empecemos con un ejemplo motivador. Considera las siguientes dos parcelas de dispersión.
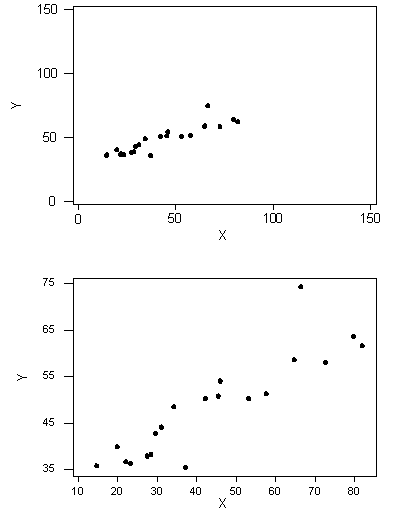
Podemos ver que en ambos casos, la dirección de la relación es positiva y la forma de la relación es lineal. ¿Qué pasa con la fuerza? Recordemos que la fortaleza de una relación es la medida en que los datos siguen su forma.
Aprender haciendo: Fuerza de correlación
El propósito de este ejemplo fue ilustrar cómo evaluar la fuerza de la relación lineal solo a partir de una gráfica de dispersión es problemática, ya que nuestro juicio podría verse afectado por la escala en la que se trazan los valores. Este ejemplo, por lo tanto, proporciona una motivación para la necesidad de complementar la gráfica de dispersión con una medida numérica que medirá la fuerza de la relación lineal entre dos variables cuantitativas.
El coeficiente de correlación — r
Objetivos de aprendizaje
LO 4.26: Explicar las limitaciones del coeficiente de correlación de Pearson (r) como medida de la asociación entre dos variables cuantitativas.
Objetivos de aprendizaje
LO 4.27: En el caso especial de una relación lineal, interpretar el coeficiente de correlación de Pearson (r) en contexto.
La medida numérica que evalúa la fuerza de una relación lineal se denomina coeficiente de correlación, y se denota con r. Vamos a:
- dar una definición de la correlación r,
- discutir el cálculo de r,
- explicar cómo interpretar el valor de r, y
- hablar de algunas de las propiedades de r.
Coeficiente de correlación: El coeficiente de correlación (r) es una medida numérica que mide la fuerza y dirección de una relación lineal entre dos variables cuantitativas.
Cálculo: r se calcula utilizando la siguiente fórmula:
\(r=\dfrac{1}{n-1} \sum_{i=1}^{n}\left(\dfrac{x_{i}-\bar{x}}{s_{x}}\right)\left(\dfrac{y_{i}-\bar{y}}{s_{y}}\right)\)
Sin embargo, el cálculo de la correlación (r) no es el foco de este curso. Utilizaremos un paquete de estadísticas para calcular r por nosotros, y el énfasis de este curso estará en la interpretación de su valor.
Interpretación
Una vez obtenido el valor de r, su interpretación con respecto a la fuerza de las relaciones lineales es bastante sencilla, como ilustran estas imágenes:
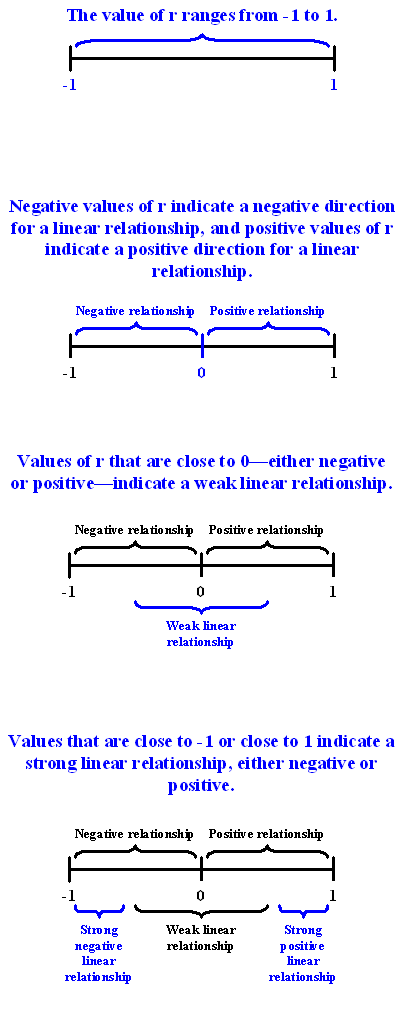
Para tener una mejor idea de cómo el valor de r se relaciona con la fuerza de la relación lineal, eche un vistazo a los siguientes applets.
Applets Interactivos: Correlación
Si va a utilizar la correlación a menudo en su investigación, le insto encarecidamente a que lea la siguiente discusión más detallada de correlación.
(Opcional) Lectura Exterior: Coeficientes de Correlación (≈ 2700 palabras)
Ahora que entendemos el uso de r como medida numérica para evaluar la dirección y la fuerza de las relaciones lineales entre variables cuantitativas, veremos algunos ejemplos.
EJEMPLO: Visibilidad de la Señal
Anteriormente, utilizamos la gráfica de dispersión a continuación para encontrar una relación lineal negativa entre la edad de un conductor y la distancia máxima a la que era legible una señal de carretera. ¿Y la fuerza de la relación? Resulta que la correlación entre las dos variables es r = -0.793.
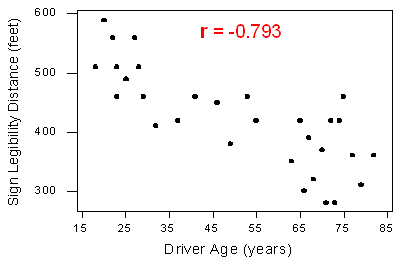
Desde r < 0, confirma que la dirección de la relación es negativa (aunque realmente no necesitábamos r para decirnos eso). Dado que r está relativamente cerca de -1, sugiere que la relación es moderadamente fuerte. En contexto, la correlación negativa confirma que la distancia máxima a la que un signo es legible generalmente disminuye con la edad. Dado que el valor de r indica que la relación lineal es moderadamente fuerte, pero no perfecta, podemos esperar que la distancia máxima varíe algo, incluso entre conductores de la misma edad.
EJEMPLO: Cursos de Estadística
Un departamento de estadística está interesado en dar seguimiento al progreso de sus alumnos desde el ingreso hasta la graduación. Como parte del estudio, el departamento tabula el desempeño de 10 alumnos en un curso introductorio y en un curso de nivel superior requerido para la graduación. ¿Cuál es la relación entre los promedios de los estudiantes en los dos cursos? Aquí está la gráfica de dispersión para los datos:
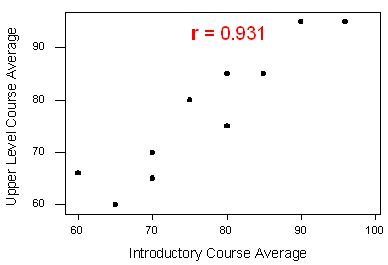
La gráfica de dispersión sugiere una relación que es positiva en dirección, lineal en forma y parece bastante fuerte. El valor de la correlación que encontramos entre las dos variables es r = 0.931, que está muy cerca de 1, y así confirma que efectivamente la relación lineal es muy fuerte.
Comentarios:
- Obsérvese que en ambos ejemplos complementamos la gráfica de dispersión con la correlación (r). Ahora que tenemos la correlación (r), ¿por qué todavía necesitamos mirar una gráfica de dispersión al examinar la relación entre dos variables cuantitativas?
- El coeficiente de correlación solo puede interpretarse como la medida de la fuerza de una relación lineal, por lo que necesitamos el diagrama de dispersión para verificar que la relación efectivamente se ve lineal. Este punto y su importancia serán más claros después de examinar algunas propiedades de r.
¿Recibí esto? Coeficiente de Correlación
Propiedades de r
Ahora discutiremos e ilustraremos varias propiedades importantes del coeficiente de correlación como medida numérica de la fuerza de una relación lineal.
- La correlación no cambia cuando cambian las unidades de medida de cualquiera de las variables. Es decir, si cambiamos las unidades de medida de la variable explicativa y/o la variable de respuesta, esto no tiene efecto sobre la correlación (r).
Para ilustrar esto, a continuación se presentan dos versiones del diagrama de dispersión de la relación entre la distancia de legibilidad del signo y la edad del conductor:
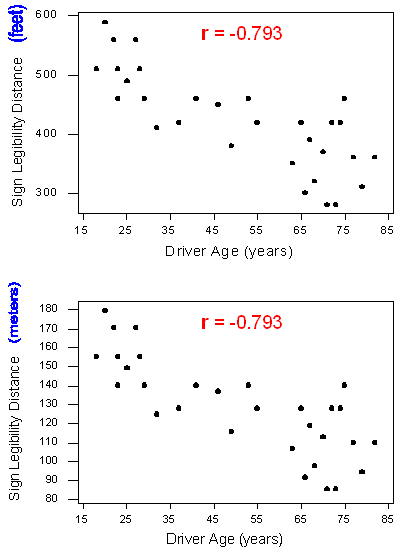
La gráfica de dispersión superior muestra los datos originales donde se miden las distancias máximas en pies. La gráfica de dispersión inferior muestra la misma relación, pero con distancias máximas cambiadas a metros. Observe que los valores Y han cambiado, pero las correlaciones son las mismas. Este es un ejemplo de cómo cambiar las unidades de medida de la variable de respuesta no tiene efecto sobre r, pero como señalamos anteriormente, lo mismo es cierto para cambiar las unidades de la variable explicativa, o de ambas variables.
Este podría ser un buen lugar para comentar que la correlación (r) es “sin unidades”. Es sólo un número.
- La correlación solo mide la fuerza de una relación lineal entre dos variables. Ignora cualquier otro tipo de relación, por fuerte que sea. Por ejemplo, considere la relación entre el uso promedio de combustible al conducir una distancia fija en un automóvil y la velocidad a la que conduce el automóvil:
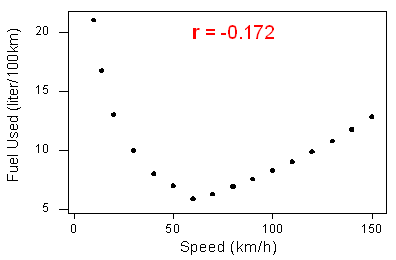
Nuestros datos describen una relación no lineal bastante simple (a veces llamada curvilínea): la cantidad de combustible consumido disminuye rápidamente a un mínimo para un automóvil que conduce 60 kilómetros por hora, y luego aumenta gradualmente para velocidades superiores a 60 kilómetros por hora. La relación es muy fuerte, ya que las observaciones parecen encajar perfectamente en la curva.
Aunque la relación es fuerte, la correlación r = -0.172 indica una relación lineal débil. Esto tiene sentido considerando que los datos no se adhieren estrechamente a una forma lineal:
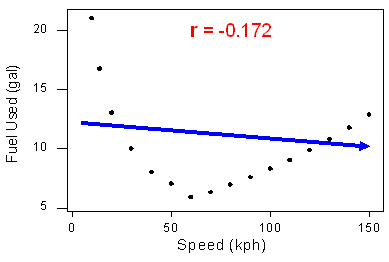
- La correlación por sí misma no es suficiente para determinar si una relación es lineal o no. Para ver esto, consideremos el estudio que examinó el efecto de los incentivos monetarios en la tasa de retorno de los cuestionarios. A continuación se muestra el diagrama de dispersión que relaciona el porcentaje de participantes que completaron una encuesta con el incentivo monetario que los investigadores prometieron a los participantes, en el que encontramos una fuerte relación no lineal (a veces llamada curvilínea):
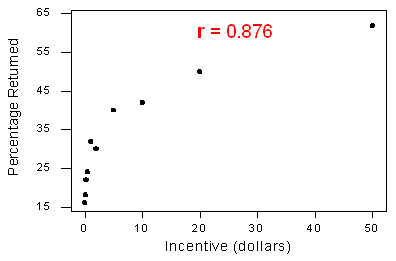
La relación es no lineal (a veces llamada curvilínea), sin embargo la correlación r = 0.876 es bastante cercana a 1.
En los dos últimos ejemplos hemos visto dos relaciones no lineales muy fuertes (a veces llamadas curvilíneas), una con una correlación cercana a 0, y otra con una correlación cercana a 1. Por lo tanto, la correlación por sí sola no indica si una relación es lineal o no. El principio importante aquí es:
¡Siempre mira los datos!
- La correlación está fuertemente influenciada por valores atípicos. Como aprenderás en las siguientes dos actividades, la forma en que el valor atípico influye en la correlación depende de si el valor atípico es consistente o no con el patrón de la relación lineal.
Applet interactivo: correlación y valores atípicos
Ojalá hayas notado que la correlación disminuye cuando creaste este tipo de valores atípicos, lo que no es consistente con el patrón de la relación.
La siguiente actividad te mostrará cómo un valor atípico que es consistente con la dirección de la relación lineal en realidad la fortalece.
Aprender haciendo: Correlación y valores atípicos (Software)
En la actividad anterior, vimos un ejemplo donde había una relación lineal positiva entre las dos variables, e incluyendo el valor atípico simplemente la “fortaleció”. Considere los datos hipotéticos mostrados por la siguiente gráfica de dispersión:
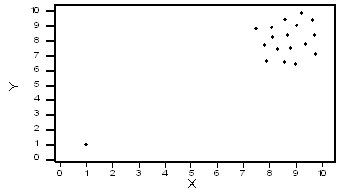
En este caso, el valor atípico bajo da una “ilusión” de una relación lineal positiva, mientras que en realidad, no existe una relación lineal entre X e Y.
Relaciones Lineales — Regresión Lineal
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.21: Para una situación de análisis de datos que involucre dos variables, determinar la (s) visualización (es) gráfica (es) apropiada (s) y/o medidas numéricas que deben usarse para resumir los datos.
Video
Vídeo: Relaciones Lineales — Regresión Lineal (5:58)
Tutoriales SAS relacionados
- 9A — (3:53) Gráfica de dispersión básica
- 9B — (2:29) Gráfica de dispersión agrupada
- 9C — (3:46) Coeficiente de correlación de Pearson
- 9D — (3:00) Regresión lineal simple — EDA
Tutoriales relacionados con SPSS
- 9A — (2:38) Gráfica de dispersión básica
- 9B — (2:54) Gráfica de dispersión agrupada
- 9C — (3:35) Coeficiente de correlación de Pearson
- 9D — (2:53) Regresión lineal simple — EDA
Resumiendo el patrón de los datos con una línea
Objetivos de aprendizaje
LO 4.28: En el caso especial de una relación lineal, interpretar la pendiente de la línea de regresión y utilizar la línea de regresión para hacer predicciones.
Hasta ahora hemos utilizado la gráfica de dispersión para describir la relación entre dos variables cuantitativas, y en el caso especial de una relación lineal, hemos complementado la gráfica de dispersión con la correlación (r).
La correlación, sin embargo, no caracteriza completamente la relación lineal entre dos variables cuantitativas, solo mide la fuerza y la dirección. A menudo queremos describir con mayor precisión cómo una variable cambia con la otra (por “más precisamente”, queremos decir más que solo la dirección), o predecir el valor de la variable de respuesta para un valor dado de la variable explicativa.
Para poder hacer eso, necesitamos resumir la relación lineal con una línea que mejor se ajuste al patrón lineal de los datos. En el resto de esta sección, presentaremos una manera de encontrar tal línea, aprender a interpretarla y usarla (con cautela) para hacer predicciones.
Nuevamente, comencemos con un ejemplo motivador:
Anteriormente, se examinó la relación lineal entre la edad de un conductor y la distancia máxima a la que era legible una señal de carretera, utilizando tanto una gráfica de dispersión como el coeficiente de correlación. Supongamos que una agencia gubernamental quería predecir la distancia máxima a la que el letrero sería legible para los conductores de 60 años, y así asegurarse de que el letrero pudiera usarse de manera segura y efectiva.
¿Cómo haríamos esta predicción?
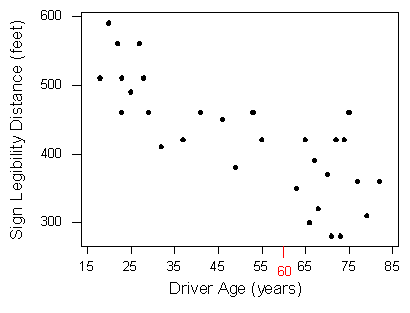
Sería útil si pudiéramos encontrar una línea (como la que se presenta en la gráfica de dispersión) que represente el patrón general de los datos, porque entonces,
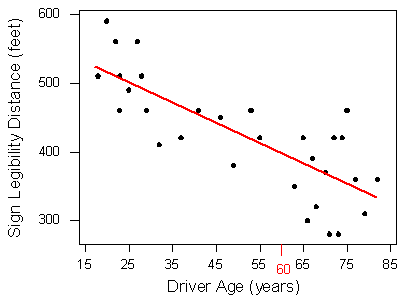
y predecir que conductores de 60 años podrían ver el letrero desde una distancia de poco menos de 400 pies simplemente usaríamos esta línea para encontrar la distancia que corresponde a una edad de 60 como esta:
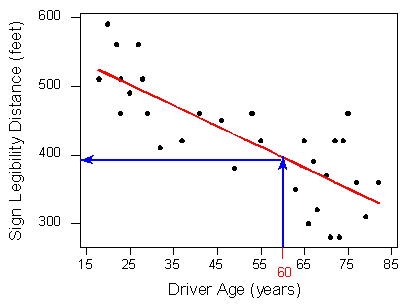
¿Cómo y por qué elegimos esta línea en particular (la que se muestra en rojo en el recorrido anterior) para describir la dependencia de la distancia máxima a la que un letrero es legible a la edad de un conductor? ¿Qué línea elegimos exactamente? Volveremos a este ejemplo una vez que podamos responder esa pregunta con un poco más de precisión.
Applets Interactivos: Regresión por Ojo
La técnica que especifica la dependencia de la variable respuesta de la variable explicativa se denomina regresión. Cuando esa dependencia es lineal (que es el caso en nuestros ejemplos en esta sección), la técnica se denomina regresión lineal. Por lo tanto, la regresión lineal es la técnica de encontrar la línea que mejor se ajuste al patrón de la relación lineal (o en otras palabras, la línea que mejor describe cómo la variable de respuesta depende linealmente de la variable explicativa).
Para entender cómo se elige tal línea, considere la siguiente versión muy simplificada del ejemplo de edad-distancia (dejamos solo 6 de los conductores en la gráfica de dispersión):
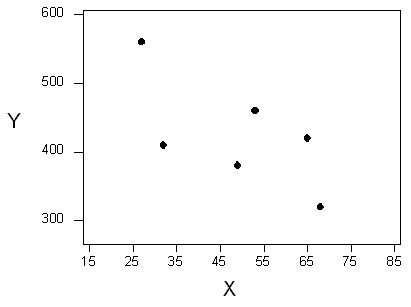
Hay muchas líneas que parecen ser buenas candidatas para ser la línea que mejor se ajuste a los datos:
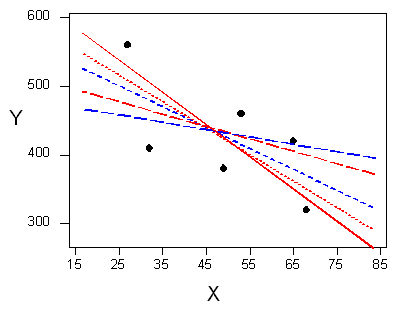
Es dudoso que todos seleccionen la misma línea en la trama anterior. Tenemos que ponernos de acuerdo en lo que entendemos por “mejor se ajusta a los datos”; es decir, tenemos que acordar un criterio por el cual seleccionaríamos esta línea. Queremos que la línea que elegimos esté cerca de los puntos de datos. Es decir, cualquiera que sea el criterio que escojamos, es mejor que de alguna manera se tengan en cuenta las desviaciones verticales de los puntos de datos de la línea, los cuales están marcados con flechas azules en la siguiente gráfica:
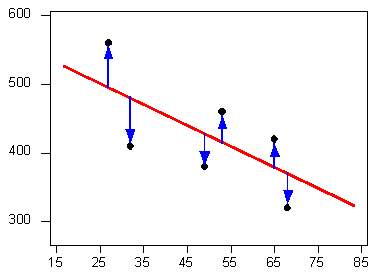
El criterio más utilizado se denomina criterio de mínimos cuadrados. Este criterio dice: Entre todas las líneas que se ven bien en tus datos, elige la que tenga la menor suma de desviaciones verticales cuadradas. Visualmente, cada desviación cuadrada está representada por el área de uno de los cuadrados en la parcela de abajo. Por lo tanto, estamos buscando la línea que tendrá el área amarilla total más pequeña.
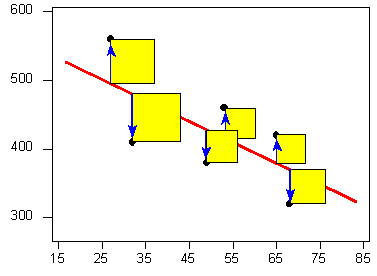
Esta línea se llama la línea de regresión de mínimos cuadrados, y, como veremos, se ajusta muy bien al patrón lineal de los datos.
Para el resto de esta lección, necesitarás sentirte cómodo con el álgebra de una línea recta. En particular necesitarás estar familiarizado con la pendiente y la intersección en la ecuación de una línea, y su interpretación.
Muchos estudiantes se preguntan: Revisión de álgebra — Ecuación lineal
Applet Interactivo: Ecuaciones Lineales — Efecto de Cambiar la Pendiente o Intercepción en la Línea
Como cualquier otra línea, la ecuación de la línea de regresión de mínimos cuadrados para resumir la relación lineal entre la variable de respuesta (Y) y la variable explicativa (X) tiene la forma: Y = a + Bx
Todo lo que tenemos que hacer es calcular la intercepción a, y la pendiente b, que aprenderemos a hacer usando software.
La pendiente de la línea de regresión de mínimos cuadrados puede interpretarse como el cambio estimado (o predicho) en el valor medio (o promedio) de la variable de respuesta cuando la variable explicativa aumenta en 1 unidad.
EJEMPLO: Edad Distancia
Revisemos nuestro ejemplo de edad-distancia y busquemos la línea de regresión de mínimos cuadrados. El siguiente resultado será útil para obtener los 5 valores que necesitamos:
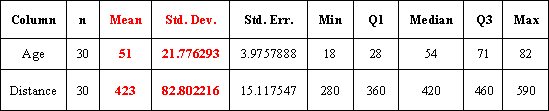
- Variable dependiente: Distancia
- Variable independiente: Edad
- Coeficiente de correlación (r) = -0.7929
- La línea de regresión de mínimos cuadrados para este ejemplo es:
Distancia\(= 576 + (-3 * \text{ Age}\)
- Esto significa que por cada incremento de 1 unidad de la variable explicativa, hay, en promedio, una disminución de 3 unidades en la variable de respuesta. La interpretación en contexto de la pendiente (-3) es, por lo tanto: En este conjunto de datos, cuando la edad aumenta en 1 año se espera que la distancia máxima promedio a la que los sujetos puedan leer un signo disminuya en 3 pies.
- Aquí está la línea de regresión trazada en la gráfica de dispersión:
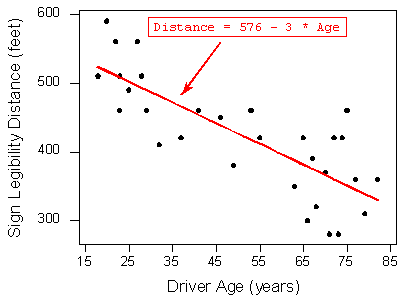
Como podemos ver, la línea de regresión se ajusta bastante bien al patrón lineal de los datos.
Volvamos ahora a nuestro ejemplo motivador, en el que queríamos predecir la distancia máxima a la que un letrero es legible para un niño de 60 años. Ahora que hemos encontrado la línea de regresión de mínimos cuadrados, esta predicción se vuelve bastante fácil:
EJEMPLO: Edad Distancia
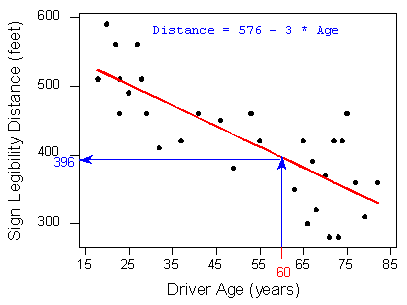
Prácticamente, lo que nos dice la cifra es que para encontrar la distancia de legibilidad predicha para un niño de 60 años, conectamos Edad = 60 en la ecuación de la línea de regresión, para encontrar que:
Distancia pronosticada = 576 + (- 3 * 60) = 396
396 pies es nuestra mejor predicción para la distancia máxima a la que un letrero es legible para un niño de 60 años.
¿Recibí esto? : Regresión lineal
Comentar sobre las predicciones:
- Supongamos que una agencia gubernamental quería diseñar un letrero apropiado para una gama aún más amplia de conductores que los que estaban presentes en el estudio original. Quieren predecir la distancia máxima a la que el letrero sería legible para un joven de 90 años. Usando nuevamente la línea de regresión de mínimos cuadrados como nuestro resumen de la dependencia lineal de las distancias sobre las edades de los conductores, la agencia predice que los conductores de 90 años pueden ver el letrero a no más de 576 + (- 3 * 90) = 306 pies:
82. La ecuación de la línea de regresión es Distancia = 576 - 3 * Edad” height="274" loading="lazy” src=” http://phhp-faculty-cantrell.sites.m...2-linear16.gif "title="La gráfica de dispersión para la Edad del Conductor vs. Distancia de Legibilidad de Signos. Las escalas de ambos ejes se han ampliado para que la línea de regresión tenga espacio a la derecha para extenderse más allá de donde existan datos. La línea de regresión es negativa, por lo que crece desde la parte superior izquierda hasta la parte inferior derecha de la parcela. Donde la línea de regresión está creando una estimación entre los datos existentes, es roja. Más allá de eso, donde no hay puntos de datos, la línea es verde. Esta área es x>82. La ecuación de la línea de regresión es Distancia = 576 - 3 * Edad” width="405">
(El segmento verde de la línea es la región de edades más allá de los 82 años, la edad del individuo más antiguo en el estudio).
Pregunta: ¿Es confiable nuestra predicción para conductores de 90 años?
Respuesta: Nuestros datos de edad originales oscilaron entre 18 (conductor más joven) y 82 (conductor más antiguo), y nuestra línea de regresión es, por lo tanto, un resumen de la relación lineal en ese rango de edad únicamente. Cuando conectamos el valor 90 en la ecuación de la línea de regresión, estamos asumiendo que la misma relación lineal se extiende más allá del rango de nuestros datos de edad (18-82) en el segmento verde. No hay justificación para tal suposición. Podría darse el caso de que la visión de los conductores mayores de 82 años se caiga más rápidamente que para los conductores más jóvenes. (es decir, la pendiente cambia de -3 a algo más negativo). Por lo tanto, nuestra predicción para la edad = 90 no es confiable.
En General
La predicción para rangos de la variable explicativa que no están en los datos se denomina extrapolación. Dado que no hay forma de saber si una relación se mantiene más allá del rango de la variable explicativa en los datos, la extrapolación no es confiable, y debe evitarse. En nuestro ejemplo, como la mayoría de los demás, la extrapolación puede llevar a predicciones muy pobres o ilógicas.
Applets interactivos: Regresión lineal
Aprender haciendo: Regresión lineal (Software)
Resumimos
- Un caso especial de la relación entre dos variables cuantitativas es la relación lineal. En este caso, una línea recta resume simple y adecuadamente la relación.
- Cuando la gráfica de dispersión muestra una relación lineal, la complementamos con el coeficiente de correlación (r), que mide la fuerza y dirección de una relación lineal entre dos variables cuantitativas. La correlación oscila entre -1 y 1. Los valores cercanos a -1 indican una fuerte relación lineal negativa, los valores cercanos a 0 indican una relación lineal débil y los valores cercanos a 1 indican una relación lineal positiva fuerte.
- La correlación es solo una medida numérica apropiada para las relaciones lineales, y es sensible a los valores atípicos. Por lo tanto, la correlación solo debe usarse como complemento de una gráfica de dispersión (después de mirar los datos).
- El criterio más utilizado para encontrar una línea que resume el patrón de una relación lineal es “mínimos cuadrados”. La línea de regresión de mínimos cuadrados tiene la menor suma de desviaciones verticales cuadradas de los puntos de datos de la línea.
- La pendiente de la línea de regresión de mínimos cuadrados puede interpretarse como el cambio estimado (o predicho) en el valor medio (o promedio) de la variable de respuesta cuando la variable explicativa aumenta en 1 unidad.
- La intersección de la línea de regresión de mínimos cuadrados es el valor promedio de la variable de respuesta cuando la variable explicativa es cero. Así, esto solo es de interés si tiene sentido que la variable explicativa sea cero Y hemos observado datos en ese rango (variable explicativa alrededor de cero) en nuestra muestra.
- La línea de regresión de mínimos cuadrados predice el valor de la variable de respuesta para un valor dado de la variable explicativa. La extrapolación es la predicción de valores de la variable explicativa que caen fuera del rango de los datos. Dado que no hay forma de saber si una relación se mantiene más allá del rango de la variable explicativa en los datos, la extrapolación no es confiable, y debe evitarse.

