CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.
En la sección anterior, discutimos variables aleatorias discretas: variables aleatorias cuyos valores posibles son una lista de números distintos. Hablamos sobre sus distribuciones de probabilidad, medias y desviaciones estándar.
Ahora estamos pasando a discutir variables aleatorias continuas: variables aleatorias que pueden tomar cualquier valor en un intervalo, de modo que no se puedan enumerar todos sus valores posibles (como altura, peso, temperatura, tiempo, etc.)
Resulta que la mayoría de los métodos para tratar variables aleatorias continuas requieren un nivel matemático superior al que necesitábamos para tratar variables aleatorias discretas. En su mayor parte, el cálculo de probabilidades asociadas a una variable aleatoria continua, y su media y desviación estándar, requiere conocimiento del cálculo, y está fuera del alcance de este curso.
Lo que haremos en esta parte es discutir la idea detrás de la distribución de probabilidad de una variable aleatoria continua, y mostrar cómo los cálculos que involucran tales variables se vuelven bastante complicados ¡muy rápido!
Luego pasaremos a una clase especial de variables aleatorias continuas — variables aleatorias normales. Las variables aleatorias normales son muy comunes y juegan un papel muy importante en la inferencia estadística.
Terminaremos esta sección presentando una conexión importante entre la variable aleatoria binomial (la variable aleatoria discreta especial que presentamos anteriormente) y la variable aleatoria normal (la variable aleatoria continua especial que presentaremos aquí).
La distribución de probabilidad de una variable aleatoria continua
Objetivos de aprendizaje
LO 6.16: Explicar cómo se usa una función de densidad para encontrar probabilidades que involucren variables aleatorias continuas.
Para cambiar nuestro enfoque de variables discretas a variables aleatorias continuas, primero consideremos el histograma de probabilidad a continuación para el tamaño de zapato de machos adultos. Deje que X represente estos tamaños de zapatos. Así, X es una variable aleatoria discreta, ya que las tallas de zapatos solo pueden tomar valores enteros y medios numéricos, nada en el medio.
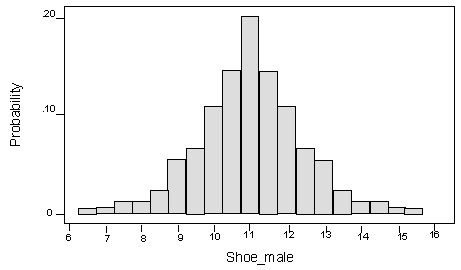
Recordemos que en todos los histogramas de probabilidad anteriores que hemos visto, los valores X fueron números enteros. Así, el ancho de cada barra fue de 1. La altura de cada barra fue la misma que la probabilidad para su valor X correspondiente. Debido al principio que establece la suma de probabilidades de todos los resultados posibles en el espacio muestral debe ser 1, las alturas de todos los rectángulos en el histograma deben sumar a 1. Esto significó que la zona también era de 1.
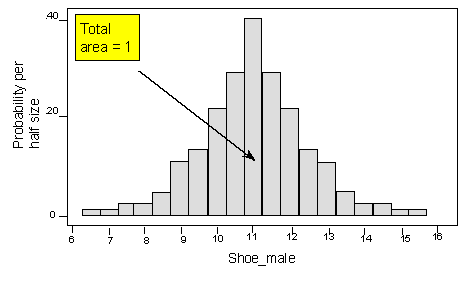
Este histograma utiliza medias tallas. Deseamos mantener el área = 1, pero aún queremos que la escala horizontal represente medias tallas. Por lo tanto, debemos ajustar la escala vertical del histograma. Como es, el área total de los rectángulos del histograma sería .50 veces la suma de las probabilidades, ya que el ancho de cada barra es .50. Así, el área es .50 (1) = .50. Si doblamos la escala vertical, el área se duplicará y será 1, tal como queremos. Esto significa que estamos cambiando la escala vertical de “Probabilidad” a “Probabilidad por medio tamaño”. La forma y la escala horizontal permanecen sin cambios.
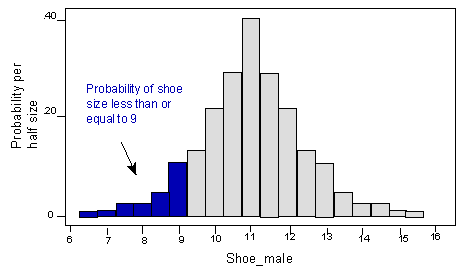
Ahora podemos decir la probabilidad de que el tamaño del zapato tome un valor en cualquier intervalo, simplemente encontrando el área de los rectángulos sobre ese intervalo. Por ejemplo, el área de los rectángulos hasta e incluyendo 9 muestra la probabilidad de tener una talla de zapato menor o igual a 9.
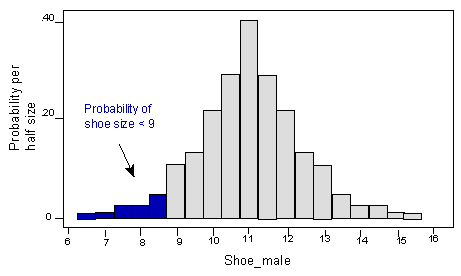
Recordemos que para una variable aleatoria discreta como el tamaño del zapato, la probabilidad se ve afectada por si queremos una desigualdad estricta o no. Por ejemplo, el área -y la probabilidad correspondiente- se reduce si solo consideramos tallas de zapatos estrictamente inferiores a 9:
Transición a Variables Aleatorias Continuas
Ahora vamos a estar haciendo la transición de variables aleatorias discretas a continuas. Recordemos que las variables aleatorias continuas representan mediciones y pueden tomar cualquier valor dentro de un intervalo.
Para nuestro ejemplo de talla de zapatos, esto significaría medir tallas de zapatos en unidades más pequeñas, como décimas o centésimas. A medida que aumenta el número de intervalos, el ancho de las barras se vuelve cada vez más estrecho, y la gráfica se acerca a una curva suave.
Para ilustrar esto, las siguientes gráficas representan dos pasos en este proceso de estrechamiento de los anchos de los intervalos. Específicamente, los anchos de intervalo son 0.25 y 0.10.
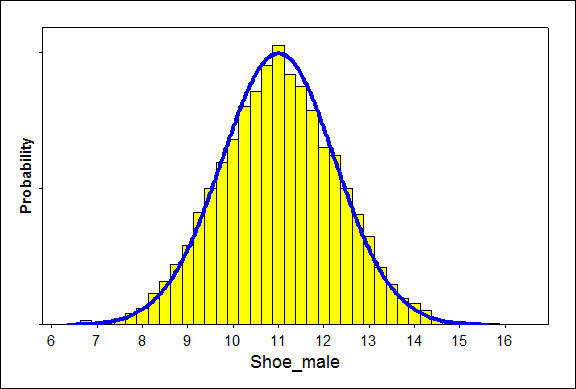
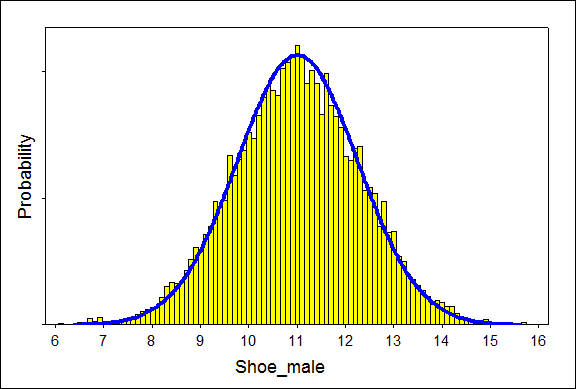
Usaremos estas curvas suaves para representar las distribuciones de probabilidad de variables aleatorias continuas. Esta idea se discutirá con más detalle en la siguiente página.
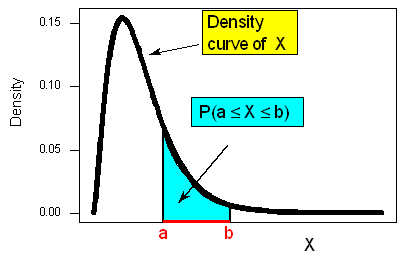
Ahora considere otra variable aleatoria X = longitud del pie de los machos adultos. A diferencia del tamaño del zapato, esta variable no se limita a valores distintos y separados, ya que las longitudes de los pies pueden tomar cualquier valor sobre un rango continuo de posibilidades, por lo que no podemos presentar esta variable con un histograma de probabilidad o una tabla. La distribución de probabilidad de la longitud del pie (o cualquier otra variable aleatoria continua) puede ser representada por una curva suave llamada curva de densidad de probabilidad.
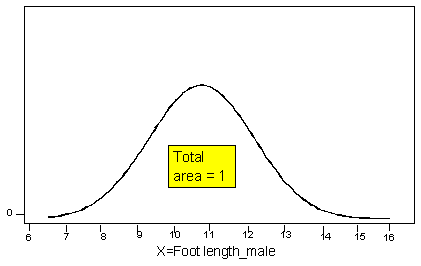
Al igual que el histograma de probabilidad modificado anterior, el área total bajo la curva de densidad es igual a 1, y la curva representa probabilidades por área.
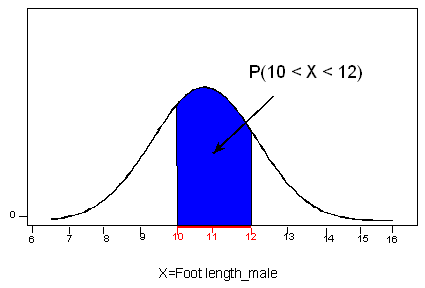
La probabilidad de que X obtenga valores en cualquier intervalo está representada por el área por encima de este intervalo y por debajo de la curva de densidad. En nuestro ejemplo de longitud de pie, si nuestro intervalo de interés está entre 10 y 12 (marcado en rojo abajo), y nos gustaría saber P (10 < X < 12), la probabilidad de que un macho elegido aleatoriamente tenga una longitud de pie entre 10 y 12 pulgadas, tendremos que encontrar el área por encima de nuestro intervalo de interés (10,12) y por debajo de nuestra curva de densidad, sombreada en azul:
Si, por ejemplo, nos interesa P (X < 9), la probabilidad de que un macho elegido aleatoriamente tenga una longitud de pie inferior a 9 pulgadas, tendremos que encontrar el área sombreada en azul a continuación:
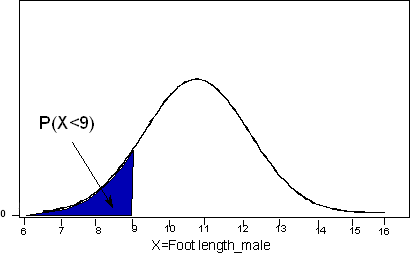
Comentarios:
- Hemos visto que para una variable aleatoria discreta como el tamaño del zapato, si tenemos una desigualdad estricta o no importa a la hora de resolver probabilidades. Por el contrario, para una variable aleatoria continua como la longitud del pie, la probabilidad de una longitud del pie menor o igual a 9 será la misma que la probabilidad de una longitud del pie estrictamente inferior a 9. Es decir, P (X < 9) = P (X ≤ 9) .Visualmente, en términos de nuestra curva de densidad, el área bajo la curva hasta e incluyendo un punto determinado es la misma que el área hasta y excluyendo el punto, porque no hay área sobre un solo punto. Conceptualmente, debido a que una variable aleatoria continua tiene infinitamente muchos valores posibles, ¡técnicamente la probabilidad de que ocurra un solo valor es cero!
- Ahora debería quedar claro por qué el área total bajo cualquier curva de densidad de probabilidad debe ser 1. El área total bajo la curva representa P (X obtiene un valor en el intervalo de sus posibles valores). Claramente, de acuerdo a las reglas de probabilidad esto debe ser 1, o siempre cierto.
- Las curvas de densidad, como los histogramas de probabilidad, pueden tener cualquier forma imaginable siempre que el área total debajo de la curva sea 1.
Vamos a resumir
La distribución de probabilidad de una variable aleatoria continua está representada por una curva de densidad de probabilidad.
La probabilidad de que X obtenga un valor en cualquier intervalo de interés es el área por encima de este intervalo y por debajo de la curva de densidad.
Ahora que vemos cómo se encuentran las probabilidades para las variables aleatorias continuas, entendemos por qué es más complicado que encontrar probabilidades en el caso discreto. Como puede atestiguar cualquiera que haya estudiado cálculo, encontrar el área bajo una curva puede ser difícil. El enfoque general es el uso de integrales. Para aquellos de ustedes que sí estudiaron cálculo, lo siguiente debería ser familiar...
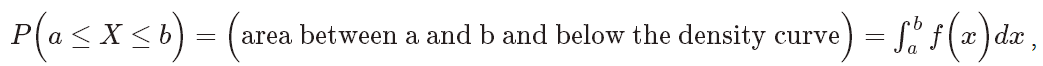
donde f (x) representa la curva de densidad.
Para los que no estudiaron el cálculo, no se preocupen por ello. Este tipo de cálculo está definitivamente más allá del alcance de este curso.
En este curso, encontraremos varias curvas de densidad importantes, las de variables aleatorias normales, t variables aleatorias, variables aleatorias chi-cuadradas y F variables aleatorias. Las distribuciones normal y t tienen forma de campana (pico simple y simétrico) como la curva de densidad en el ejemplo de longitud del pie; las distribuciones chi-cuadrado y F son de pico único y sesgadas a la derecha, como en la figura anterior.
En lugar de empantanarse en el cálculo de resolver áreas bajo curvas, encontraremos probabilidades para las variables aleatorias mencionadas anteriormente consultando tablas. Además, el software estadístico proporciona automáticamente dichas probabilidades en el contexto apropiado.
En la siguiente sección, estudiaremos con más profundidad una de esas variables aleatorias, la variable aleatoria normal, y veremos cómo podemos encontrar probabilidades asociadas a ella usando software y tablas.











