Variables aleatorias discretas
- Última actualización
- 31 oct 2022
- Guardar como PDF
- Page ID
- 151240
( \newcommand{\kernel}{\mathrm{null}\,}\)
CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.
Reseña:
Video
Vídeo: Variables Aleatorias Discretas (22:40 Total)
Comenzamos con variables aleatorias discretas: variables cuyos valores posibles son una lista de valores distintos. Para decidir sobre alguna notación, volvamos a ver el ejemplo de lanzamiento de monedas:
Una moneda justa se arroja dos veces.
- Que la variable aleatoria X sea el número de colas que obtenemos en este experimento aleatorio.
- En este caso, los posibles valores que X puede asumir son
- 0 (si obtenemos HH),
- 1 (si obtiene HT o TH),
- y 2 (si obtenemos TT).
Notación
Si queremos encontrar la probabilidad de que el evento “obtenga 1 cola”, escribiremos: P (X = 1)
Si queremos encontrar la probabilidad de que el evento “obtenga 0 colas”, escribiremos: P (X = 0)
En general, escribiremos: P (X = x) o P (X = k) para denotar la probabilidad de que la variable aleatoria discreta X obtenga el valor x o k respectivamente.
Muchos estudiantes prefieren la segunda notación ya que hacer un seguimiento de la diferencia entre X y x puede causar confusión.
- Aquí la X representa la variable aleatoria y x o k denotan el valor de interés en el problema actual (0, 1, etc.).
- Tenga en cuenta que para las variables aleatorias usaremos una letra mayúscula, y para el valor usaremos una letra minúscula.
Plan de sección
La forma en que se organiza esta sección sobre variables aleatorias discretas es muy similar a la forma en que organizamos nuestra discusión sobre una variable cuantitativa en la unidad de Análisis Exploratorio de Datos.
Se separará en cuatro secciones.
- Primero discutiremos la distribución de probabilidad de una variable aleatoria discreta, formas de mostrarla y cómo usarla para encontrar probabilidades de interés.
- Luego pasaremos a hablar sobre la media y desviación estándar de una variable aleatoria discreta, que son medidas del centro y dispersión de su distribución.
- Concluiremos esta parte discutiendo una clase especial y muy común de variable aleatoria discreta: la variable aleatoria binomial.
Distribuciones de probabilidad
Objetivos de aprendizaje
LO 6.12: Utilice la distribución de probabilidad para una variable aleatoria discreta para encontrar la probabilidad de eventos de interés.
Cuando aprendimos a encontrar probabilidades aplicando los principios básicos, generalmente nos enfocamos en un solo resultado o evento en particular, como la probabilidad de obtener exactamente una cola cuando se arroja una moneda dos veces, o la probabilidad de obtener un 5 cuando se enrolla un dado.
Ahora que hemos dominado la solución de los problemas de probabilidad individuales, procederemos a mirar el panorama general considerando todos los valores posibles de una variable aleatoria discreta, junto con sus probabilidades asociadas.
Esta lista de posibles valores y probabilidades se denomina distribución de probabilidad de la variable aleatoria.
Comentarios:
- En la unidad de Análisis Exploratorio de Datos de este curso, a menudo observamos la distribución de los valores de la muestra en un conjunto de datos cuantitativos. Mostraríamos los valores con un histograma, y los resumiríamos reportando su media.
- En esta sección, cuando observamos la distribución de probabilidad de una variable aleatoria, consideramos todos sus valores posibles y sus probabilidades generales de ocurrencia.
- Así, tenemos en mente una población entera de valores para una variable. Cuando los mostramos con un histograma o los resumimos con una media, estos representan una población de valores, no una muestra.
- La distinción entre muestra y población es un concepto esencial en la estadística, ya que un objetivo último es sacar conclusiones sobre valores desconocidos para una población, con base en lo que se observa en la muestra.
En los ejemplos que siguen a veces ilustraremos cómo se crea la distribución de probabilidad.
Lo hacemos para demostrar la utilidad de las reglas de probabilidad que discutimos anteriormente y para ilustrar claramente cómo se pueden crear distribuciones de probabilidad.
Como estamos más enfocados en los métodos basados en datos, a menudo se le dará una distribución de probabilidad basada en datos en lugar de construir la distribución de probabilidad teórica basada en voltear monedas o experimentos de probabilidad clásicos similares.
Recordemos nuestro primer ejemplo, cuando introdujimos la idea de una variable aleatoria. En este ejemplo lanzamos una moneda dos veces.
EJEMPLO: Voltear una moneda dos veces
¿Cuál es la distribución de probabilidad de X, donde la variable aleatoria X es el número de colas que aparecen en dos tiradas de una moneda justa?
Primero notamos que dado que la moneda es justa, cada uno de los cuatro resultados HH, HT, TH, TT en el espacio muestral S es igualmente probable, y así cada uno tiene una probabilidad de 1/4.
(Alternativamente, se puede aplicar el principio de multiplicación para encontrar la probabilidad de que cada resultado sea 1/2 * 1/2 = 1/4.)
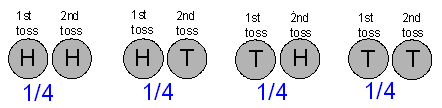
X toma el valor 0 solo para el resultado HH, por lo que la probabilidad de que X = 0 sea 1/4.
X toma el valor 1 para los resultados HT o TH. Por el principio de suma, la probabilidad de que X = 1 sea 1/4 + 1/4 = 1/2.
Por último, X toma el valor 2 solo para el resultado TT, por lo que la probabilidad de que X = 2 sea 1/4.
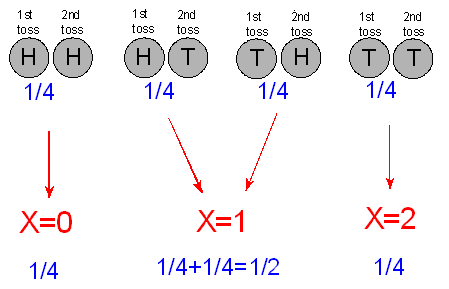
La distribución de probabilidad de la variable aleatoria X se resume fácilmente en una tabla:
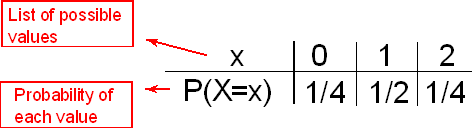
Como se mencionó anteriormente, escribimos “P (X = x)” para denotar “la probabilidad de que la variable aleatoria X tome el valor x”.
La manera de interpretar esta tabla es:
- X toma los valores 0, 1, 2 y P (X = 0) = 1/4, P (X = 1) = 1/2, P (X = 2) = 1/4.
Obsérvese que los eventos del tipo (X = x) están sujetos a los principios de probabilidad establecidos anteriormente, y nos proporcionarán una forma de explorar sistemáticamente el comportamiento de las variables aleatorias.
En particular, ahora se establecerán los dos primeros principios en el contexto de distribuciones de probabilidad de variables aleatorias.
La ley de gas ideal es fácil de recordar y aplicar en la resolución de problemas, siempre y cuando obtenga los valores adecuados a Cualquier distribución de probabilidad de una variable aleatoria discreta debe satisfacer:
1. 0≤P(X=x)≤1
2. ∑xP(X=x)=1
La distribución de probabilidad para dos volteos de una moneda fue lo suficientemente simple como para construir a la vez.
Para experimentos aleatorios más complicados, es común construir primero una tabla de todos los resultados y sus probabilidades, luego usar el principio de adición para condensar esa información en la tabla de distribución de probabilidad real.
EJEMPLO: Voltear una Moneda Tres Veces
Una moneda se arroja tres veces. Que la variable aleatoria X sea el número de colas.
Encuentra la distribución de probabilidad de X.
Seguiremos el mismo razonamiento que usamos en el ejemplo anterior:
Primero, especificamos los 8 resultados posibles en S, junto con el número y la probabilidad de ese resultado.
- Debido a que todos son igualmente probables, cada uno tiene probabilidad 1/8.
- Alternativamente, por el principio de multiplicación, cada secuencia particular de tres caras de moneda tiene probabilidad 1/2 * 1/2 * 1/2 = 1/8.
Entonces averiguamos cuál es el valor de X (número de colas) para cada posible resultado.
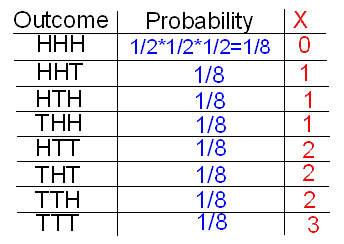
A continuación, utilizamos el principio de adición para afirmar que
- P (X = 1) = P (HHT o HTH o THH) = P (HHT) + P (HTH) + P (THH) = 1/8 + 1/8 + 1/8 = 3/8.
- De igual manera, P (X = 2) = P (HTT o THT o TTH) = 3/8.
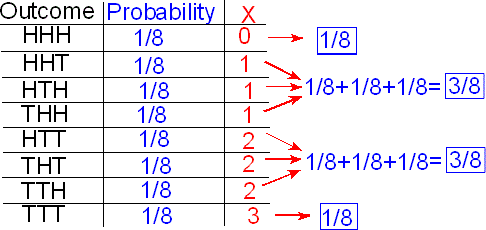
La distribución de probabilidad resultante es:
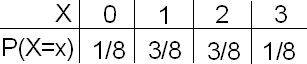
En los dos ejemplos anteriores, necesitábamos especificar las distribuciones de probabilidad nosotros mismos, con base en las circunstancias físicas de la situación.
En algunas situaciones, la distribución de probabilidad puede especificarse con una fórmula.
Dicha fórmula debe ser congruente con las limitaciones impuestas por las leyes de probabilidad, de manera que la probabilidad de cada resultado debe estar entre 0 y 1, y las probabilidades de todos los resultados posibles en conjunto deben sumar a 1.
Esto lo veremos con la distribución binomial.
Histogramas de Probabilidad
Aprendimos a mostrar la distribución de valores muestrales para una variable cuantitativa con un histograma en el que el eje horizontal representaba el rango de valores en la muestra.
- El eje vertical representaba la frecuencia o frecuencia relativa (a veces dada como porcentaje) de los valores de muestra que se producen en ese intervalo.
- El ancho de cada rectángulo en el histograma fue un intervalo, o parte de los valores posibles para la variable cuantitativa.
- La altura de cada rectángulo fue la frecuencia (o frecuencia relativa) para ese intervalo.
Del mismo modo, podemos mostrar la distribución de probabilidad de una variable aleatoria con un histograma de probabilidad.
- El eje horizontal representa el rango de todos los valores posibles de la variable aleatoria
- El eje vertical representa las probabilidades de esos valores.
Aquí un ejemplo de un histograma de probabilidad.
(Tales probabilidades no siempre van en aumento; simplemente pasan a ser así en este ejemplo).
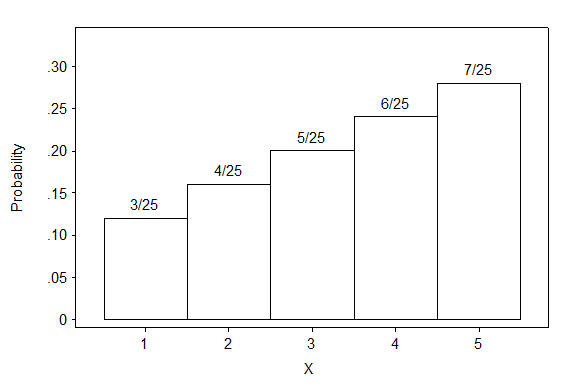
Área de un histograma de probabilidad
Observe que cada rectángulo en el histograma tiene un ancho de 1 unidad. La altura de cada rectángulo es la probabilidad de que ocurra.
Por lo tanto, el área de cada rectángulo es base tiempos altura, que para estos rectángulos es 1 veces su probabilidad para cada valor de X.
Esto significa que para distribuciones de probabilidad de variables aleatorias discretas, la suma de las áreas de todos los rectángulos es la misma que la suma de todas las probabilidades. El área total = 1.
Para distribuciones de probabilidad de variables aleatorias discretas, esto equivale a la propiedad de que la suma de todas las probabilidades debe ser igual a 1.
Aprende haciendo: Distribuciones de probabilidad
Encontrar probabilidades
Hemos visto cómo se crean las distribuciones de probabilidad. Ahora es el momento de utilizarlos para encontrar probabilidades.
EJEMPLO: Cambio de Mayores
Se encuestó una muestra aleatoria de egresados de la tercera edad justo antes de graduarse. Una pregunta que se hizo es:
¿Cuántas veces cambiaste de especialización?
Los resultados se muestran en una distribución de probabilidad.

Usando esta distribución de probabilidad, podemos responder preguntas de probabilidad como:
¿Cuál es la probabilidad de que un senior seleccionado al azar haya cambiado de especialización más de una vez?
Esto se puede escribir como P (X > 1).
Podemos encontrar esta probabilidad sumando las probabilidades individuales apropiadas en la distribución de probabilidad.
- P (X > 1)
- = P (X = 2) + P (X = 3) + P (X = 4) + P (X = 5)
- = 0.23 + 0.09 + 0.02 + 0.01
- = 0.35
Como acaba de ver en este ejemplo, debemos prestar atención a la redacción de la pregunta de probabilidad.
Las palabras clave que nos decían qué valores usar para X son más que.
A continuación se aclararán y reforzarán las palabras clave y sus significados.
Palabras clave
Comencemos con algunas situaciones cotidianas usando al menos y como máximo.
Supongamos que alguien te dijo: “Necesito que escribas al menos 10 páginas para un trabajo final”.
- ¿Qué significa esto?
- Significa que 10 páginas es la cantidad más pequeña que vas a escribir.
- Es decir, escribirás 10 o más páginas para el trabajo de término.
- Esto sería lo mismo que decir, “no menos de 10 páginas”.
- Entonces, por ejemplo, escribir 9 páginas sería inaceptable.
Por otro lado, suponga que está considerando la cantidad de hijos que tendrá. Quieres como máximo 3 hijos.
- Esto quiere decir que 3 hijos es lo más que deseas tener.
- En otras palabras, tendrás 3 o menos
- Esto sería lo mismo que decir, “no más de 3 niños”.
- Entonces, por ejemplo, no querrías tener 4 hijos.
En la siguiente tabla se da una lista de algunas palabras clave para conocer.
Supongamos que una variable aleatoria X tenía valores posibles de 0 a 5.
| Palabras clave | Significado | Símbolos | Valores para X |
|---|---|---|---|
| más de 2 | estrictamente más grande que 2 | X > 2 | 3, 4, 5 |
| no más de 2 | 2 o menos | X ≤ 2 | 0, 1, 2 |
| menos de 2 | estrictamente más pequeños que 2 | X < 2 | 0, 1 |
| no menos de 2 | 2 o más | X ≥ 2 | 2, 3, 4, 5 |
| al menos 2 | 2 o más | X ≥ 2 | 2, 3, 4, 5 |
| a lo sumo 2 | 2 o menos | X ≤ 2 | 0, 1, 2 |
| exactamente 2 | 2, ni más ni menos, solo 2 | X = 2 | 2 |
Antes de pasar a la siguiente sección sobre las medias y varianzas de una distribución de probabilidad, volvamos a revisar el ejemplo de mayores cambiantes:
EJEMPLO: Cambio Mayor

Pregunta: Con base en esta distribución, ¿cree que sería inusual cambiar mayores 2 o más veces?
Respuesta:
- P (X ≥ 2) = 0.35.
- Entonces, 35% de las veces un estudiante cambia de carrera 2 o más veces.
- Esto quiere decir que no es inusual hacerlo.
Pregunta: ¿Crees que sería inusual cambiar mayores 4 o más veces?
Respuesta:
- P (X ≥ 4) = 0.03.
- Entonces, el 3% de las veces un estudiante cambia de carrera 4 o más veces.
- Esto quiere decir que es bastante inusual hacerlo.
¡Incluso podemos responder preguntas más difíciles usando nuestras reglas de probabilidad!
Pregunta: ¿Cuál es la probabilidad de cambiar mayores solo una vez dado al menos un cambio en mayor?
Respuesta:
- P (X = 1 | X ≥ 1) = P (X = 1 Y X ≥ 1) /P (X ≥ 1) [usando la Regla de Probabilidad 7]
- = P (X = 1) /P (X ≥ 1) [ya que el único resultado que satisface tanto X = 1 como X ≥ 1 es X = 1]
- = (0.37)/(0.37+0.23+.0.09+0.02+0.01) = 0.37/0.72 = 0.5139.
- Entonces, entre los estudiantes que cambian de especialización, 51% de estos estudiantes solo cambiarán de especialización una vez.
Después de conocer las medias y las desviaciones estándar, tendremos otra forma de responder a este tipo de preguntas.
Media de una Variable Aleatoria Discreta
Objetivos de aprendizaje
LO 6.13: Encuentra la media, varianza y desviación estándar de una variable aleatoria discreta.
En la sección Análisis Exploratorio de Datos (EDA), mostramos la distribución de una variable cuantitativa con un histograma, y la complementamos con medidas numéricas de centro y propagación.
Aquí estamos haciendo lo mismo.
- Mostramos la distribución de probabilidad de una variable aleatoria discreta con una tabla, fórmula o histograma.
- Y complementarlo con medidas numéricas del centro y propagación de la distribución de probabilidad.
Estas medidas son la media y desviación estándar de la variable aleatoria.
Esta sección se dedicará a introducir estas medidas. Como antes, comenzaremos con la medida numérica del centro, la media. Empecemos por revisitar un ejemplo que vimos en EDA.
EJEMPLO: Copa Mundial de Futbol
Recordemos que utilizamos los siguientes datos de 3 torneos de Copa Mundial (un total de 192 juegos) para introducir la idea de un promedio ponderado.
Hemos agregado una tercera columna a nuestra tabla que nos da frecuencias relativas.
| número total de goles/partido | frecuencia | frecuencia relativa |
|---|---|---|
| 0 | 17 | 17/192 = 0.089 |
| 1 | 45 | 45/192 = 0.234 |
| 2 | 51 | 51/192 = 0.266 |
| 3 | 37 | 37/192 = 0.193 |
| 4 | 25 | 25/192 = 0.130 |
| 5 | 11 | 11/192 = 0.057 |
| 6 | 3 | 3/192 = 0.016 |
| 7 | 2 | 2/192 = 0.010 |
| 8 | 1 | 1/192 = 0.005 |
La media para estos datos es:
0(17)+1(45)+2(51)+3(37)+4(25)+5(11)+6(3)+7(2)+8(1)192
Distribuyendo la división por 192 obtenemos:
0(17192)+1(45192)+2(51192)+⋯+8(1192)
Observe que la media es cada número de goles por juego multiplicado por su frecuencia relativa.
Como solemos escribir las frecuencias relativas como decimales, podemos ver que:
Número medio de goles por partido =
- 0 (0.089) + 1 (0.234) + 2 (0.266) + 3 (0.193) + 4 (0.130) + 5 (0.057) + 6 (0.016) + 7 (0.010) + 8 (0.005)
= 2.36, redondeado a dos decimales.
En Análisis Exploratorio de Datos se utilizó la media de una muestra de valores cuantitativos —su promedio aritmético— para indicar el centro de su distribución. También vimos cómo se utilizó una media ponderada cuando teníamos una tabla de frecuencias. Estas frecuencias se pueden cambiar a frecuencias relativas.
Así que esencialmente estamos usando el enfoque de frecuencia relativa para encontrar probabilidades. Podemos usar esto para encontrar la media, o centro, de una distribución de probabilidad para una variable aleatoria discreta, que será un promedio ponderado de sus valores; cuanto más probable sea un valor, más peso obtendrá.
Como siempre, es importante distinguir entre una muestra concreta de valores observados para una variable versus una población abstracta de todos los valores tomados por una variable aleatoria a largo plazo.
Mientras que denotamos la media de una muestra como barra x, ahora denotamos la media de una variable aleatoria usando la letra griega mu con un subíndice para la variable aleatoria que estamos usando.
Veamos cómo se hace esto mirando un ejemplo específico.
EJEMPLO: Línea de Producción Xavier
La línea de producción de Xavier produce un número variable de piezas defectuosas en una hora, con probabilidades que se muestran en esta tabla:
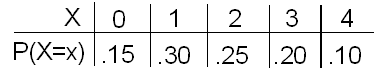
¿Cuántas piezas defectuosas se producen normalmente en una hora en la línea de producción de Xavier? Si resumimos los posibles valores de X, cada uno ponderado con su probabilidad, tenemos
μX=0(0.15)+1(0.30)+2(0.25)+3(0.20)+4(0.10)=1.8
Aquí está la definición general de la media de una variable aleatoria discreta:
En general, para cualquier variable aleatoria discreta X con distribución de probabilidad
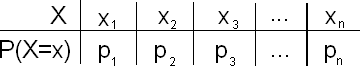
La media de X se define como
μX=x1p1+x2p2+…+xnpn=∑ni=1xipi
- En general, la media de una variable aleatoria nos dice su valor promedio de “largo plazo”.
- A veces se le conoce como el valor esperado de la variable aleatoria.
Si bien “valor esperado” es un término común, e incluso preferido en el campo de la estadística, esta expresión puede ser algo engañosa, porque en muchos casos es imposible que una variable aleatoria iguale realmente su valor esperado.
Por ejemplo, el número medio de goles para un partido de fútbol de la Copa Mundial es de 2.36. Pero nunca podemos esperar que un solo juego resulte en 2.36 goles, ya que no es posible marcar una fracción de un gol. Más bien, 2.36 es el promedio a largo plazo de todos los partidos de fútbol de la Copa Mundial.
En el caso de la línea de producción de Xavier, el número medio de piezas defectuosas producidas en una hora es 1.8. Pero el número real de piezas defectuosas producidas en una hora determinada nunca puede ser igual a 1.8, ya que debe tomar valores de números enteros.
Para tener una mejor idea de la media de una variable aleatoria, extendamos el ejemplo de partes defectuosas:
EJEMPLO: Líneas de Producción de Xavier e Yves
Recordemos la distribución de probabilidad de la variable aleatoria X, que representa el número de piezas defectuosas en una hora producidas por la línea de producción de Xavier.
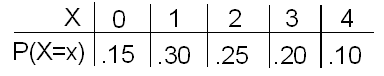
El número de piezas defectuosas producidas cada hora por la línea de producción de Yves es una variable aleatoria Y con la siguiente distribución de probabilidad:
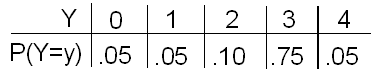
Observa ambas distribuciones de probabilidad. Tanto X como Y toman los mismos valores posibles (0, 1, 2, 3, 4).
Sin embargo, son muy diferentes en la forma en que se distribuye la probabilidad entre estos valores.
Aprender haciendo: Comparando Distribuciones de Probabilidad #1
¿Conseguí esto? : Media de Variable Aleatoria Discreta
Varianza y desviación estándar de una variable aleatoria discreta
Objetivos de aprendizaje
LO 6.13: Encuentra la media, varianza y desviación estándar de una variable aleatoria discreta.
En Análisis Exploratorio de Datos, se utilizó la media de una muestra de valores cuantitativos (su promedio aritmético, barra x) para indicar el centro de su distribución, y la desviación estándar para indicar la distancia típica de los valores de la muestra a su media.
Describimos el centro de una distribución de probabilidad para una variable aleatoria reportando su media que denotamos con la letra griega mu.
Ahora nos gustaría establecer una medida acompañante de spread.
Nuestra medida de propagación seguirá reportando la distancia típica de los valores de sus medias, pero para distinguir la dispersión de una población de todos los valores de una variable aleatoria de la (s) dispersión (es) de valores de muestra, denotaremos la desviación estándar de la variable aleatoria X con la minúscula griega” sigma”, y usa un subíndice para recordarnos cuál es la variable de interés (puede haber más de una en problemas posteriores):
También nos enfocaremos con más frecuencia que antes en la desviación estándar cuadrada, llamada varianza, porque algunas reglas importantes que necesitamos invocar son en términos de varianza en lugar de desviación estándar.
EJEMPLO: Línea de Producción Xavier
Recordemos que el número de piezas defectuosas producidas cada hora por la línea de producción de Xavier es una variable aleatoria X con la siguiente distribución de probabilidad:
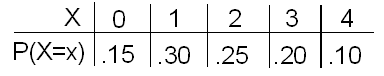
Se encontró que el número medio de piezas defectuosas producidas por hora era 1.8.
Obviamente, hay variación sobre esta media: algunas horas se producen tan pocas como 0 piezas defectuosas, mientras que en otras horas se producen hasta 4.
Por lo general, ¿a qué distancia cae el número de piezas defectuosas de la media de 1.8?
Como lo hicimos para la dispersión de los valores muestrales, medimos la dispersión de una variable aleatoria calculando la raíz cuadrada de la desviación cuadrada promedio de la media.
Ahora “promedio” es un promedio ponderado, donde a los valores más probables de la variable aleatoria se les da en consecuencia más peso.
Comencemos con la varianza, o desviación cuadrada promedio de la media, y luego tomemos su raíz cuadrada para encontrar la desviación estándar:
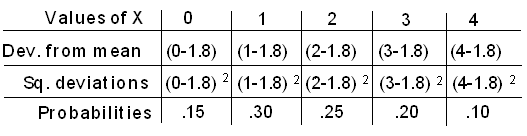
\ begin {alineado}
\ text {Varianza} &=\ sigma_ {X} ^ {2} =( 0-1.8) ^ {2} (0.15) + (1-1.8) ^ {2} (0.30) + (2-1.8) ^ {2} (0.25)\\
&+ (3-1.8) ^ {2} (0.20) + (4-1.8) ^ {2} (0.1)\\
&= 1.46
\ end {alineado}
desviación estándar=σX=√1.46=1.21
¿Cómo interpretamos la desviación estándar de X?
- La línea de producción de Xavier produce un promedio de 1.80 piezas defectuosas por hora.
- El número de piezas defectuosas varía de hora a hora; típicamente (o, en promedio), se encuentra aproximadamente a 1.21 de distancia de la media de 1.80.
Aquí está la definición formal:
En general, para cualquier variable aleatoria discreta X con distribución de probabilidad
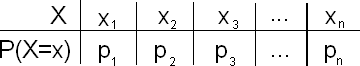
La varianza de X se define como
\ begin {alineado}
\ sigma_ {X} ^ {2} &=\ izquierda (x_ {1} -\ mu_ {X}\ derecha) ^ {2} p_ {1} +\ izquierda (x_ {2} -\ mu_ {X}\ derecha) ^ {2} p_ {2} +\ ldots+\ izquierda (x_ {n} -\ mu_ {X}\ derecha) ^ {2} p_ {n}\\
&=\ suma_ {i=1} ^ {n}\ izquierda (x_ {i} -\ mu_ {X}\ derecha) ^ {2} p_ {i}
\ fin {alineado}
También hay una fórmula de “atajo” que es más rápida para el cálculo manual. En la siguiente fórmula hemos bajado el subíndice para la variable en la notación. En este atajo, simplemente necesitamos
- cuadrado cada X,
- multiplicar por la probabilidad de que X,
- luego suma esos valores.
- De ese resultado restamos el cuadrado de la media para encontrar la varianza.
Var(X)=σ2=∑ni=1[x2iP(X=xi)]−μ2
La desviación estándar es la raíz cuadrada de la varianza
σX=√σ2X
¿Conseguí esto? : Desviación estándar de una variable aleatoria discreta
El propósito de la siguiente actividad es darle una mejor intuición sobre la media y desviación estándar de una variable aleatoria.
Aprender haciendo: Comparando Distribuciones de Probabilidad #2
EJEMPLO: Líneas de Producción de Xavier e Yves
Recordemos la distribución de probabilidad de la variable aleatoria X, que representa el número de piezas defectuosas por hora producidas por la línea de producción de Xavier, y la distribución de probabilidad de la variable aleatoria Y, que representa el número de piezas defectuosas por hora producidas por la línea de producción de Yves:
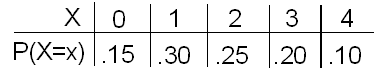
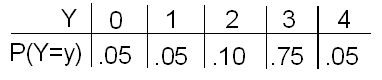
Observe cuidadosamente ambas distribuciones de probabilidad. Tanto X como Y toman los mismos valores posibles (0, 1, 2, 3, 4).
Sin embargo, son muy diferentes en la forma en que se distribuye la probabilidad entre estos valores. Vimos antes que esto marca una diferencia en los medios:
μX=1.8
μY=2.7
Ahora queremos tener una idea de cómo las diferentes distribuciones de probabilidad impactan sus desviaciones estándar.
Recordemos que la desviación estándar de una variable aleatoria puede interpretarse como una distancia típica (o la media a largo plazo) entre el valor de X y su media.
Aprender haciendo: Comparando Distribuciones de Probabilidad #3
Entonces, 75% del tiempo Y asumirá un valor (3) que está muy cerca de su media (2.7), mientras que X asumirá un valor (2) que está cerca de su media (1.8) y mucho menos frecuentemente, solo el 25% del tiempo.
El promedio a largo plazo, entonces, de la distancia entre los valores de Y y su media será mucho menor que el promedio a largo plazo de la distancia entre los valores de X y su media.
Por lo tanto
σY<σX=1.21
En realidad tenemos
σY=0.85
Así podemos sacar la siguiente conclusión:
La línea de producción de Yves produce un promedio de 2.70 piezas defectuosas por hora.
El número de piezas defectuosas varía de hora a hora; típicamente (o, en promedio), se encuentra aproximadamente a 0.85 lejos de 2.70.
Aquí están los histogramas para las líneas de producción:
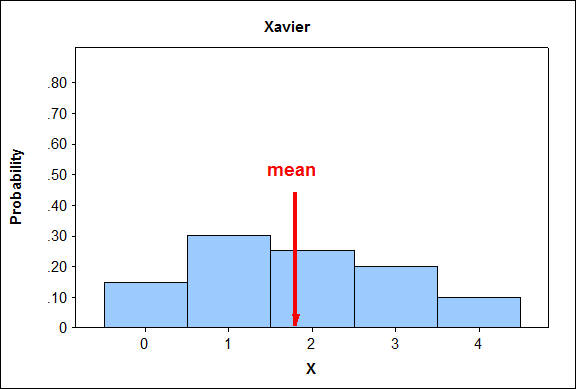
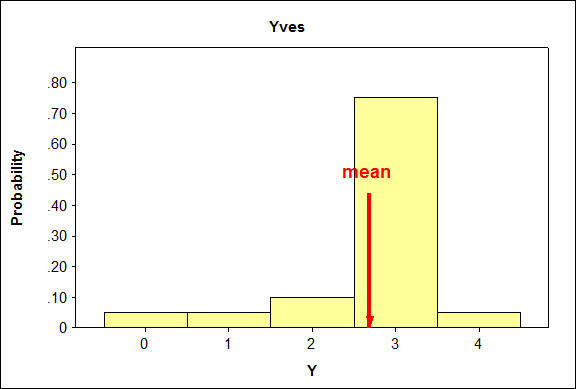
Cuando comparamos distribuciones, la distribución en la que es más probable encontrar valores que están más alejados de la media tendrá una desviación estándar mayor.
De igual manera, la distribución en la que es menos probable encontrar valores que están más alejados de la media tendrá la menor desviación estándar.
¿Conseguí esto? : Desviación estándar de una variable aleatoria discreta #2
Comentario:
Como hemos dicho anteriormente, usar la media y la desviación estándar nos da otra forma de evaluar qué valores de una variable aleatoria son inusuales.
Para distribuciones razonablemente simétricas, cualquier valor de una variable aleatoria que se encuentre dentro de 2 o 3 desviaciones estándar de la media se consideraría ordinario (no inusual).
Para cualquier distribución, es inusual que los valores caigan fuera de 3 o 4 desviaciones estándar, dependiendo de su definición de “inusual”.
EJEMPLO: ¿La línea de producción de Xavier es inusual
Mirando una vez más la distribución de probabilidad para la línea de producción de Xavier:
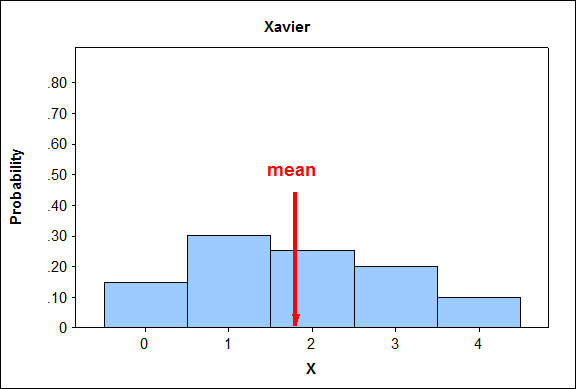
¿Se consideraría inusual tener 4 piezas defectuosas por hora?
Sabemos que la media es 1.8 y la desviación estándar es 1.21.
Los valores ordinarios están dentro de 2 (o 3) desviaciones estándar de la media.
- 1.8 — 2 (1.21) = -0.62 y
- 1.8 + 2 (1.21) = 4.22.
Esto nos da un intervalo de -0.62 a 4.22.
Como no podemos tener un número negativo de piezas defectuosas, el intervalo es esencialmente de 0 a 4.22.
Debido a que 4 está dentro de este intervalo, se consideraría ordinario. Por lo tanto, no es inusual.
¿Se consideraría inusual no tener piezas defectuosas?
El cero se encuentra dentro de 2 desviaciones estándar de la media, por lo que no se consideraría inusual no tener partes defectuosas.
La siguiente actividad reforzará esta idea.
Aprende haciendo: ¿inusual o no?

