2.10: Prueba Cochran-Mantel-Haenszel
- Page ID
- 149230
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Para usar la prueba Cochran—Mantel—Haenszel cuando tienes datos de\(2\times 2\) tablas que has repetido en diferentes momentos o ubicaciones. Te dirá si tienes una diferencia consistente en proporciones a través de las repeticiones.
Cuándo usarlo
Use la prueba Cochran—Mantel—Haenszel (que a veces se llama prueba Mantel—Haenszel) para pruebas repetidas de independencia. La situación más común es que tienes múltiples\(2\times 2\) tablas de independencia; estás analizando el tipo de experimento que analizarías con una prueba de independencia, y has hecho el experimento varias veces o en múltiples ubicaciones. Hay tres variables nominales: las dos variables de la\(2\times 2\) prueba de independencia, y la tercera variable nominal que identifica las repeticiones (como diferentes tiempos, diferentes ubicaciones o diferentes estudios). Hay versiones de la prueba Cochran—Mantel—Haenszel para cualquier número de filas y columnas en las pruebas individuales de independencia, pero rara vez se usan y no las voy a cubrir.
Por ejemplo, digamos que has encontrado varios cientos de calentadores de poliéster de punto rosa que han estado escondidos en un almacén desde que pasaron de moda en 1984. Tú decides ver si reducen el dolor de la osteoartritis de tobillo al mantener los tobillos calientes. En el invierno, reclutas\(36\) voluntarios con artritis de tobillo, asignas al azar\(20\) a usar los calentadores de piernas debajo de su ropa en todo momento mientras que el otro\(16\) no usa los calentadores de piernas, luego de un mes les preguntas si sus tobillos están libres de dolor o no. Con solo un conjunto de personas, tendrías dos variables nominales (calentadores de piernas vs. control, sin dolor vs. dolor), cada una con dos valores, por lo que analizarías los datos con la prueba exacta de Fisher.
No obstante, digamos que repites el experimento en primavera, con\(50\) nuevos voluntarios. Después en el verano vuelves a repetir el experimento, con\(28\) nuevos voluntarios. Podrías simplemente sumar todos los datos juntos y hacer la prueba exacta de Fisher sobre el\(114\) total de personas, pero sería mejor mantener separados cada uno de los tres experimentos. A lo mejor los calentadores de piernas trabajan en invierno pero no en verano, o tal vez tu primer grupo de voluntarios tuvo peor artritis que tu segundo y tercer grupo. Además, aunar diferentes estudios juntos puede mostrar una diferencia “significativa” en proporciones cuando no la hay, o incluso mostrar lo contrario de una verdadera diferencia. Esto se conoce como la paradoja de Simpson. Por estas razones, es mejor analizar pruebas repetidas de independencia usando la prueba Cochran-Mantel-Haenszel.
Hipótesis nula
La hipótesis nula es que las proporciones relativas de una variable son independientes de la otra variable dentro de las repeticiones; en otras palabras, no hay diferencia consistente en proporciones en las\(2\times 2\) tablas. Para nuestro experimento imaginario de calentadores de piernas, la hipótesis nula sería que la proporción de personas que sienten dolor era la misma para los portadores de calentadores de piernas y los que no los usan, después de controlar para la época del año. La hipótesis alternativa es que la proporción de personas que sienten dolor fue diferente para los portadores de calentador de piernas y no calentadores de piernas.
Técnicamente, la hipótesis nula de la prueba Cochran—Mantel—Haenszel es que las odds ratios dentro de cada repetición son iguales a\(1\). La razón de probabilidades es igual a\(1\) cuando las proporciones son las mismas, y la razón de probabilidades es diferente de\(1\) cuando las proporciones son diferentes entre sí. Creo que las proporciones son más fáciles de entender que las odds ratios, así que pondré todo en términos de proporciones. Pero si estás en un campo como la epidemiología donde este tipo de análisis es común, probablemente vas a tener que pensar en términos de odds ratios.
Cómo funciona la prueba
Si etiquetas los cuatro números en una\(2\times 2\) prueba de independencia así:
\[\begin{matrix} a & b\\ c & d \end{matrix}\]
y
\[(a+b+c+d)=n\]
puede escribir la ecuación para el estadístico de prueba Cochran—Mantel—Haenszel así:
\[X_{MH}^{2}=\frac{\left \{ \left | \sum \left [ a-(a+b)(a+c)/n \right ] \right | -0.5\right \}^2}{\sum (a+b)(a+c)(b+d)(c+d)/(n^3-n^2)}\]
El numerador contiene el valor absoluto de la diferencia entre el valor observado en una celda (\(a\)) y el valor esperado bajo la hipótesis nula\((a+b)(a+c)/n\), por lo que el numerador es la suma cuadrada de desviaciones entre los valores observados y esperados. No importa cómo organices las\(2\times 2\) tablas, cualquiera de los cuatro valores se puede utilizar como\(a\). Se resta el\(0.5\) como una corrección de continuidad. El denominador contiene una estimación de la varianza de las diferencias cuadradas.
El estadístico de prueba,\(X_{MH'}^{2}\), se hace más grande a medida que las diferencias entre los valores observados y esperados aumentan, o a medida que la varianza se hace más pequeña (principalmente debido a que el tamaño de la muestra aumenta). Es chi-cuadrado distribuido con un grado de libertad.
Diferentes fuentes presentan la fórmula para la prueba Cochran—Mantel—Haenszel en diferentes formas, pero todas son algebraicamente equivalentes. La fórmula que he mostrado aquí incluye la corrección de continuidad (restando\(0.5\) en el numerador), lo que debería hacer que el\(P\) valor sea más preciso. Algunos programas realizan la prueba Cochran—Mantel—Haenszel sin la corrección de continuidad, así que asegúrese de especificar si la utilizó al informar sus resultados.
Supuestos
Además de probar la hipótesis nula, la prueba Cochran-Mantel-Haenszel también produce una estimación de la razón de probabilidades común, una forma de resumir qué tan grande es el efecto cuando se agrupa entre las diferentes repeticiones del experimento. Esto requiere asumir que la razón de probabilidades es la misma en las diferentes repeticiones. Puedes probar esta suposición usando la prueba de Breslow-Day, que no voy a explicar en detalle; su hipótesis nula es que las odds ratios son iguales a través de las diferentes repeticiones.
Si algunas repeticiones tienen una gran diferencia de proporción en una dirección, y otras repeticiones tienen una gran diferencia en proporciones pero en sentido contrario, la prueba Cochran-Mantel-Haenszel puede dar un resultado no significativo. Entonces, cuando recibas una prueba Cochran-Mantel-Haenszel no significativa, debes realizar una prueba de independencia en cada\(2\times 2\) mesa por separado e inspeccionar los\(P\) valores individuales y la dirección de la diferencia para ver si algo así está sucediendo. En nuestro ejemplo de calentador de piernas, si la proporción de personas con dolor de tobillo era mucho menor para los usuarios de calentadores de piernas en el invierno, pero mucho mayor en el verano, y la prueba de Cochran-Mantel-Haenszel dio un resultado no significativo, sería erróneo concluir que los calentadores de piernas no tuvieron ningún efecto. En cambio, se podría concluir que los calentadores de piernas tuvieron un efecto, simplemente fue diferente en las diferentes estaciones.
Ejemplos
Ejemplo
Cuando miras la parte posterior de la cabeza de alguien, el cabello o bien gira en sentido horario o antihorario. Lauterbach y Knight (1927) compararon la proporción de espirales en el sentido de las agujas del reloj en niños diestros y zurdos. Con solo este conjunto de personas, tendrías dos variables nominales (diestro vs. zurdo, horario vs. antihorario), cada una con dos valores, así que analizarías los datos con la prueba exacta de Fisher.
Sin embargo, varios otros grupos han realizado estudios similares sobre el verticilo y la mano del cabello (McDonald 2011):
| Grupo de estudio | Handedness | Derecha | Izquierda |
|---|---|---|---|
| niños blancos | En sentido horario | 708 | 50 |
| En sentido antihorario | 169 | 13 | |
| por ciento CCW | 19.3% | 20.6% | |
| Adultos británicos | En sentido horario | 136 | 24 |
| En sentido antihorario | 73 | 14 | |
| por ciento CCW | 34.9% | 38.0% | |
| Blancos de Pensilvania | En sentido horario | 106 | 32 |
| En sentido antihorario | 17 | 4 | |
| por ciento CCW | 13.8% | 11.1% | |
| Hombres galeses | En sentido horario | 109 | 22 |
| En sentido antihorario | 16 | 26 | |
| por ciento CCW | 12.8% | 54.2% | |
| Soldados alemanes | En sentido horario | 801 | 102 |
| En sentido antihorario | 180 | 25 | |
| por ciento CCW | 18.3% | 19.7% | |
| Niños alemanes | En sentido horario | 159 | 27 |
| En sentido antihorario | 18 | 13 | |
| por ciento CCW | 10.2% | 32.5% | |
| Nueva York | En sentido horario | 151 | 51 |
| En sentido antihorario | 28 | 15 | |
| por ciento CCW | 15.6% | 22.7% | |
| Hombres americanos | En sentido horario | 950 | 173 |
| En sentido antihorario | 218 | 33 | |
| por ciento CCW | 18.7% | 16.0% |
Podrías simplemente sumar todos los datos juntos y hacer una prueba de independencia sobre el\(4463\) total de personas, pero sería mejor mantener cada uno de los\(8\) experimentos separados. Algunos de los estudios se realizaron en niños, mientras que otros fueron en adultos; algunos eran solo hombres, mientras que otros eran hombres y mujeres; y los estudios se hicieron en personas de diferentes orígenes étnicos. La agrupación de todos estos estudios podría oscurecer diferencias importantes entre ellos.
Al analizar los datos mediante la prueba de Cochran-Mantel-Haenszel, el resultado es\(X_{MH}^{2}=6.07\),\(1d.f.\),\(P=0.014\). En general, las personas zurdas tienen una proporción significativamente mayor de espirales en sentido antihorario que las personas diestras.
Ejemplo
McDonald y Siebenaller (1989) encuestaron frecuencias alélicas en el locus Lap en el mejillón Mytilus trossulus en la costa de Oregón. En cuatro estuarios, recolectamos mejillones del interior del estuario y de un hábitat marino fuera del estuario. Hubo tres alelos comunes y un par de alelos raros; con base en resultados previos, la pregunta biológicamente interesante fue si el alelo Lap 94 era menos común dentro de los estuarios, por lo que agrupamos todos los demás alelos en un "no- Clase de 94”.
Existen tres variables nominales: alelo (\(94\)o no-\(94\)), hábitat (marino o estuarino) y área (Tillamook, Yaquina, Alsea o Umpqua). La hipótesis nula es que en cada área, no hay diferencia en la proporción de alelos de Lap 94 entre los hábitats marinos y estuarinos.
Esta tabla muestra el número de alelos\(94\) y no\(94\) alelos en cada ubicación. Hay una menor proporción de\(94\) alelos en la ubicación estuarina de cada estuario en comparación con la ubicación marina; quisimos saber si esta diferencia es significativa.
| Ubicación | Alelo | Marina | Estuarino |
|---|---|---|---|
| TILLAMOOK | 94 | 56 | 69 |
| no-94 | 40 | 77 | |
| por ciento 94 | 58.3% | 47.3% | |
| Yaquina | 94 | 61 | 257 |
| no-94 | 57 | 301 | |
| por ciento 94 | 51.7% | 46.1% | |
| Alsea | 94 | 73 | 65 |
| no-94 | 71 | 79 | |
| por ciento 94 | 50.7% | 45.1% | |
| Umpqua | 94 | 71 | 48 |
| no-94 | 55 | 48 | |
| por ciento 94 | 56.3% | 50.0% |
El resultado es\(X_{MH}^{2}=5.05\),\(1d.f.\),\(P=0.025\). Podemos rechazar la hipótesis nula de que la proporción de alelos Lap 94 es la misma en las localidades marinas y estuarinas.
Ejemplo
Duggal et al. (2010) hicieron un metaanálisis de estudios controlados con placebo de niacina y enfermedades cardíacas. Encontraron\(5\) estudios que cumplieron con sus criterios y buscaron revascularización coronaria en pacientes a los que se administró niacina o placebo:
| Estudiar | Revascularización | Sin revasc. | Porcentaje de revasc. | |
|---|---|---|---|---|
| GRASAS | Niacina | 2 | 46 | 4.2% |
| Placebo | 11 | 41 | 21.2% | |
| AFREGS | Niacina | 4 | 67 | 5.6% |
| Placebo | 12 | 60 | 16.7% | |
| ÁRBITRO 2 | Niacina | 1 | 86 | 1.1% |
| Placebo | 4 | 76 | 5.0% | |
| SOMBREROS | Niacina | 1 | 37 | 2.6% |
| Placebo | 6 | 32 | 15.8% | |
| CLAS 1 | Niacina | 2 | 92 | 2.1% |
| Placebo | 1 | 93 | 1.1% |
Existen tres variables nominales: niacina vs placebo, revascularización vs. no revascularización y el nombre del estudio. La hipótesis nula es que la tasa de revascularización es la misma en pacientes que reciben niacina o placebo. Los diferentes estudios tienen diferentes tasas globales de revascularización, probablemente porque utilizaron diferentes poblaciones de pacientes y buscaron revascularización después de diferentes períodos de tiempo, por lo que sería imprudente sumar los números y hacer una sola\(2\times 2\) prueba. El resultado de la prueba Cochran-Mantel-Haenszel es\(X_{MH}^{2}=12.75\),\(1d.f.\),\(P=0.00036\). Significativamente menos pacientes tratados con niacina desarrollaron revascularización coronaria.
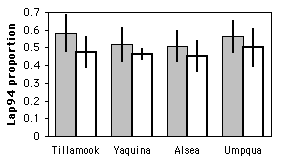
Graficando los resultados
Para graficar los resultados de una prueba de Cochran—Mantel—Haenszel, elige uno de los dos valores de la variable nominal que estás observando y traza sus proporciones en un gráfico de barras, utilizando barras de dos patrones diferentes.
Pruebas similares
A veces, la prueba Cochran—Mantel—Haenszel se llama simplemente la prueba Mantel—Haenszel. Esto es confuso, ya que también hay una prueba de homogeneidad de odds ratios llamada prueba Mantel—Haenszel, y una prueba de independencia Mantel—Haenszel para una\(2\times 2\) tabla. A Mantel y Haenszel (1959) se les ocurrió una modificación bastante menor de la idea básica de Cochran (1954), por lo que parece apropiado (y algo menos confuso) darle crédito a Cochran a nombre de esta prueba.
Si tienes al menos seis\(2\times 2\) mesas, y solo te interesa la dirección de las diferencias en proporciones, no el tamaño de las diferencias, podrías hacer una prueba de signos.
La prueba Cochran-Mantel—Haenszel para variables nominales es análoga a una prueba de anova bidireccional o t pareada para una variable de medición, o una prueba de rango firmado de Wilcoxon para datos de rango. En el ejemplo de artritis-calentadores de piernas, si midió el dolor de tobillo en una escala de\(10\) puntos (una variable de medición) en lugar de categorizarlo como dolor/no dolor, analizaría los datos con un anova bidireccional.
Cómo hacer la prueba
Hoja de Cálculo
He escrito una hoja de cálculo para realizar la prueba Cochran—Mantel—Haenszel cmh.xls. Se maneja hasta\(50\)\(2\times 2\) mesas. Te da la opción de usar o no usar la corrección de continuidad; los resultados probablemente sean un poco más precisos con la corrección de continuidad. No hace la prueba Breslow-Day.
Páginas web
No estoy al tanto de ninguna página web que realice la prueba Cochran—Mantel—Haenszel.
R
El\(R\) compañero de Salvatore Mangiafico cuenta con un programa de muestra R para la prueba Cochran-Mantel-Haenszel, y también muestra cómo hacer la prueba Breslow-Day.
SAS
Aquí hay un programa SAS que usa PROC FREQ para una prueba Cochran—Mantel—Haenszel. Utiliza los datos del mejillón de arriba. En la instrucción TABLES, la variable que etiqueta las repeticiones debe ser listada primero; en este caso es “ubicación”.
DATA lap;
INPUT location $ habitat $
alelo $ count; DATALINES;
Tillamook marine 94 56
Tillamook estuarine 94 69
Tillamook marine non-94 40
Tillamook estuarine non-94 77
Yaquina marina 94 61 Estuarina
Yaquina 94 257
Yaquina marina no-94 57 Estuarina
Yaquina no-94 301
Alsea marina 94 73 Estuarina
Alsea 94 65
Alsea marine non-94 71
Alsea estuarine non-94 79
Umpqua marine 94 71
Umpqua estuarine 94 48
Umpqua marine non-94 55
Umpqua estuarine non-94 48
;
PROC FREQ data=LAP; Recuento
PESO/ZEROS;
CUADRAS UBICACIÓN*habitat*alelo/CMH;
RUN;
Hay mucha salida, pero la parte importante se ve así:
Cochran-Mantel-Haenszel Estadística (Basado en Puntuaciones de Tabla)
Estadística Hipótesis Alternativa DF Valor Prob
—
1 Correlación Noncero 1 5.3209 0.0211
2 Las puntuaciones medias de fila difieren 1 5.3209 0.0211
3 Asociación General 1 5.3209 0.0211
Para\(2\times 2\) las tablas repetidas, las tres estadísticas son idénticas; son el estadístico de chi-cuadrado Cochran—Mantel—Haenszel, sin la corrección de continuidad. Para tablas repetidas con más de dos filas o columnas, se utiliza la estadística de “asociación general” cuando los valores de las diferentes variables nominales no tienen un orden (no se pueden organizar de menor a mayor); debe usarlo a menos que tenga una buena razón para usar una de las otras estadísticas.
Los resultados también incluyen la prueba Breslow-Day de homogeneidad de odds ratios:
Prueba Breslow-Day para
la homogeneidad de las relaciones de probabilidades
—
Chi-cuadrado 0.5295
DF 3
Pr > ChiSQ 0.9124
La prueba de Breslow-Day para los datos de ejemplo no muestra evidencia significativa de heterogeneidad de odds ratios (\(X^2=0.53\),\(3d.f.\),\(P=0.91\)).
Referencias
Cochran, W.G. 1954. Algunos métodos para fortalecer las pruebas comunes de χ 2. Biometría 10:417-451.
Duggal, J.K., M. Singh, N. Atti, P.P. Singh, N. Ahmed, S. Pahwa, J. Molnar, S. Singh, S. Khosla y R. Arora. 2010. Efecto de la terapia con niacina sobre los resultados cardiovasculares en pacientes con enfermedad coronaria. Revista de Farmacología y Terapéutica Cardiovascular 15:158-166.
Lauterbach, C.E., y J.B. Knight. 1927. Variación en el verticilo del pelo de la cabeza. Diario de la Herencia 18:107-115.
Mantel, N., y W. Haenszel. 1959. Aspectos estadísticos del análisis de datos de estudios retrospectivos de la enfermedad. Revista del Instituto Nacional del Cáncer 22:719-748.
McDonald, J.H. 2011. Mitos de la genética humana. Sparky House Press, Baltimore.
McDonald, J.H. y J.F. Siebenaller. 1989. Variación geográfica similar en el locus Lap en los mejillones Mytilus trossulus y M. edulis. Evolución 43:228-231.