9.2: Medición de la bondad de ajuste
- Page ID
- 150282
Una vez que hemos construido un modelo de regresión, es natural preguntarse: ¿qué tan bueno es el modelo para explicar la variación en nuestra variable dependiente? Podemos responder a esta pregunta con una serie de estadísticas que indican ajuste del modelo”. Básicamente, estas estadísticas proporcionan medidas del grado en que las relaciones estimadas dan cuenta de la varianza en la variable dependiente, YY.
Hay varias formas de examinar qué tan bien explica el modelo” la varianza en YY. Primero, podemos examinar la covarianza de XX e YY, que es una medida general de la varianza de la muestra para XX y YY. Entonces podemos usar una medida de correlación muestral, que es la medida estandarizada de covariación. Ambas medidas proporcionan indicadores del grado en que la variación en XX puede explicar la variación en YY. Finalmente, podemos examinar R2R2, también conocido como el coeficiente de determinación, que es la medida estándar de la bondad de ajuste para los modelos de OLS.
9.2.1 Covarianza y correlaciones de la muestra
La covarianza muestral para un modelo de regresión simple se define como:
SXY=σ (Xi−¯X) (Y−¯Y) n−1 (9.5) (9.5) SXY=σ (Xi−X¯) (Y−Y¯) n−1
Intuitivamente, esta medida te dice, en promedio, si un valor mayor de XX (relativo a su media) está asociado con un valor mayor o menor de YY. ¿La asociación es negativa o positiva? La covarianza se puede obtener simplemente en R usando la función the cov.
Sxy <- cov(ds.omit$ideol, ds.omit$glbcc_risk)
Sxy## [1] -3.137767El problema con la covarianza es que su magnitud dependerá completamente de las escalas utilizadas para medir XX e YY. Es decir, no es estándar, y su significado variará dependiendo de qué es lo que se esté midiendo. Para comparar la covariación muestral entre diferentes muestras y diferentes medidas, podemos usar la correlación muestral.
La correlación muestral, rr, se encuentra dividiendo SXYSXY por el producto de las desviaciones estándar de XX, SXSX y YY, SYSY.
r=SxySxSY=σ (Xi−¯X) (Y−¯Y) √σ (Xi−¯X) 2σ (Y−¯Y) 2 (9.6) (9.6) R=Sxysxsy=σ (Xi−X¯) (Yi−Y¯) σ (Xi−X¯) 2σ (Yi−Y¯) 2
Para calcular esto en R, primero hacemos un objeto para SXSX y SYSY usando la función sd.
Sx <- sd(ds.omit$ideol)
Sx## [1] 1.7317Sy <- sd(ds.omit$glbcc_risk)
Sy## [1] 3.070227Entonces para encontrar rr:
r <- Sxy/(Sx*Sy)
r## [1] -0.5901706Para comprobarlo podemos utilizar la función cor en R.
rbyR <- cor(ds.omit$ideol, ds.omit$glbcc_risk)
rbyR## [1] -0.5901706Entonces, ¿qué significa el coeficiente de correlación? Los valores van de +1 a -1, con un valor de +1 significa que existe una relación positiva perfecta entre XX y YY. Cada incremento de incremento en XX se corresponde con un incremento constante en YY — con todas las observaciones alineadas ordenadamente en una pendiente positiva. Un coeficiente de correlación de -1, o una relación negativa perfecta, indicaría que cada incremento de incremento en XX corresponde a una disminución constante en YY — o una línea inclinada negativamente. Un coeficiente de correlación de cero no describiría ninguna relación entre XX y YY.
9.2.2 Coeficiente de Determinación: R2R2
La medida de bondad de ajuste más utilizada para los modelos OLS es R2R2. R2R2 se deriva de tres componentes: la suma total de cuadrados, la suma explicada de cuadrados y la suma residual de cuadrados. R2R2 es la relación de ESS (suma explicada de cuadrados) a TSS (suma total de cuadrados).
Componentes de R2R2
- Suma total de cuadrados (TSS): La suma de la varianza cuadrada de YY
- Suma residual de cuadrados (RSS): La varianza de YY no contabilizada por el modelo
- Explicación de la suma de cuadrados (ESS): La varianza de YY contabilizada en el modelo. Es la diferencia entre el TSS y el RSS.
- R2R2: La proporción de la varianza total de YY explicada por el modelo o la relación de ESSESS a TSSTSS
R2=ESSTSS=TSS−RSSTSS=1−RSSTSSR2=ESSTSS=TSS−RSSTSS=1−RSSTSS
Los componentes de R2R2 se ilustran en la Figura\(\PageIndex{1}\). Como se muestra, para cada observación YiYi, la variación alrededor de la media puede descomponerse en lo que es “explicado” por la regresión y aquello que no lo es. En la Figura\(\PageIndex{1}\), la desviación entre la media de YY y el valor predicho de YY, ^YY^, es la proporción de la variación de YiYi que puede explicarse (o predecirse) por la regresión. Eso se muestra como una línea azul. La desviación del valor observado de YiYi del valor predicho ^YY^ (también conocido como el residual, como se discutió en el capítulo anterior) es la desviación inexplicable, mostrada en rojo. En conjunto, la variación explicada e inexplicable conforman la variación total de YiYi alrededor de la media ^YY^.
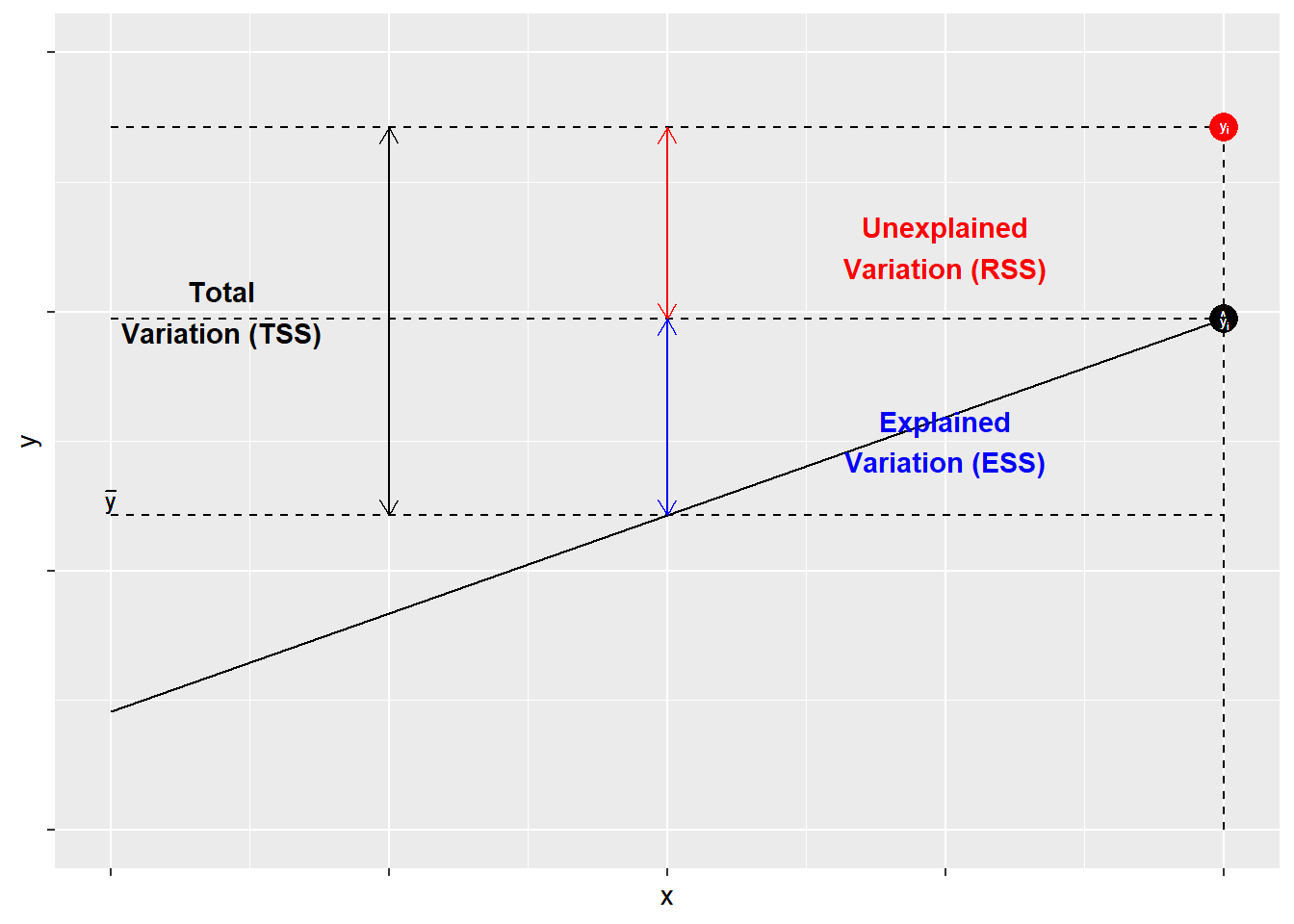
Para calcular R2R2 “a mano” en R, primero debemos determinar la suma total de cuadrados, que es la suma de las diferencias al cuadrado de los valores observados de YY a partir de la media de YY, σ (Y−¯Y) 2σ (Yi−Y¯) 2. Usando R, podemos crear un objeto llamado TSS.
TSS <- sum((ds.omit$glbcc_risk-mean(ds.omit$glbcc_risk))^2)
TSS## [1] 23678.85Recuerde que R2R2 es la relación de la suma explicada de cuadrados a la suma total de cuadrados (ESS/TSS). Por lo tanto, para calcular R2R2 necesitamos crear un objeto llamado RSS, la suma cuadrada de los residuos de nuestro modelo.
RSS <- sum(ols1$residuals^2)
RSS## [1] 15431.48A continuación, creamos un objeto llamado ESS, que es igual a TSS-RSS.
ESS <- TSS-RSS
ESS## [1] 8247.376Finalmente, calculamos el R2R2.
R2 <- ESS/TSS
R2## [1] 0.3483013Nota—felizmente— que el R2R2 calculado por “a mano” en R coincide con los resultados proporcionados por el comando summary.
Los valores para R2R2 pueden variar de cero a 1. En el caso de regresión simple, un valor de 1 indica que el coeficiente modelado (BB) “da cuenta” de toda la variación en YY. Dicho de otra manera, todas las desviaciones cuadradas en YiYi alrededor de la media (^YY^) están en ESS, sin ninguna en el residual (RSS). 16 Un valor de cero indicaría que todas las desviaciones en YiYi alrededor de la media están en RSS —todas residuales o error”. Nuestro ejemplo muestra que la variación en la ideología política (nuestro XX) representa aproximadamente el 34.8 por ciento de la variación en nuestra medida del riesgo percibido del cambio climático (YY).
9.2.3 Visualización de Regresión Bivariada
El ggplot2 el paquete proporciona un mecanismo para visualizar el efecto de la variable independiente, ideología, sobre la variable dependiente, riesgo percibido de cambio climático. Agregar geom_smooth calculará y visualizará una línea de regresión que representa la relación entre su IV y DV mientras minimiza la suma residual de cuadrados. Gráficamente (Figura\(\PageIndex{2}\)), vemos como un individuo se vuelve más conservador (ideología = 7), su percepción del riesgo de calentamiento global disminuye.
ggplot(ds.omit, aes(ideol, glbcc_risk)) +
geom_smooth(method = lm)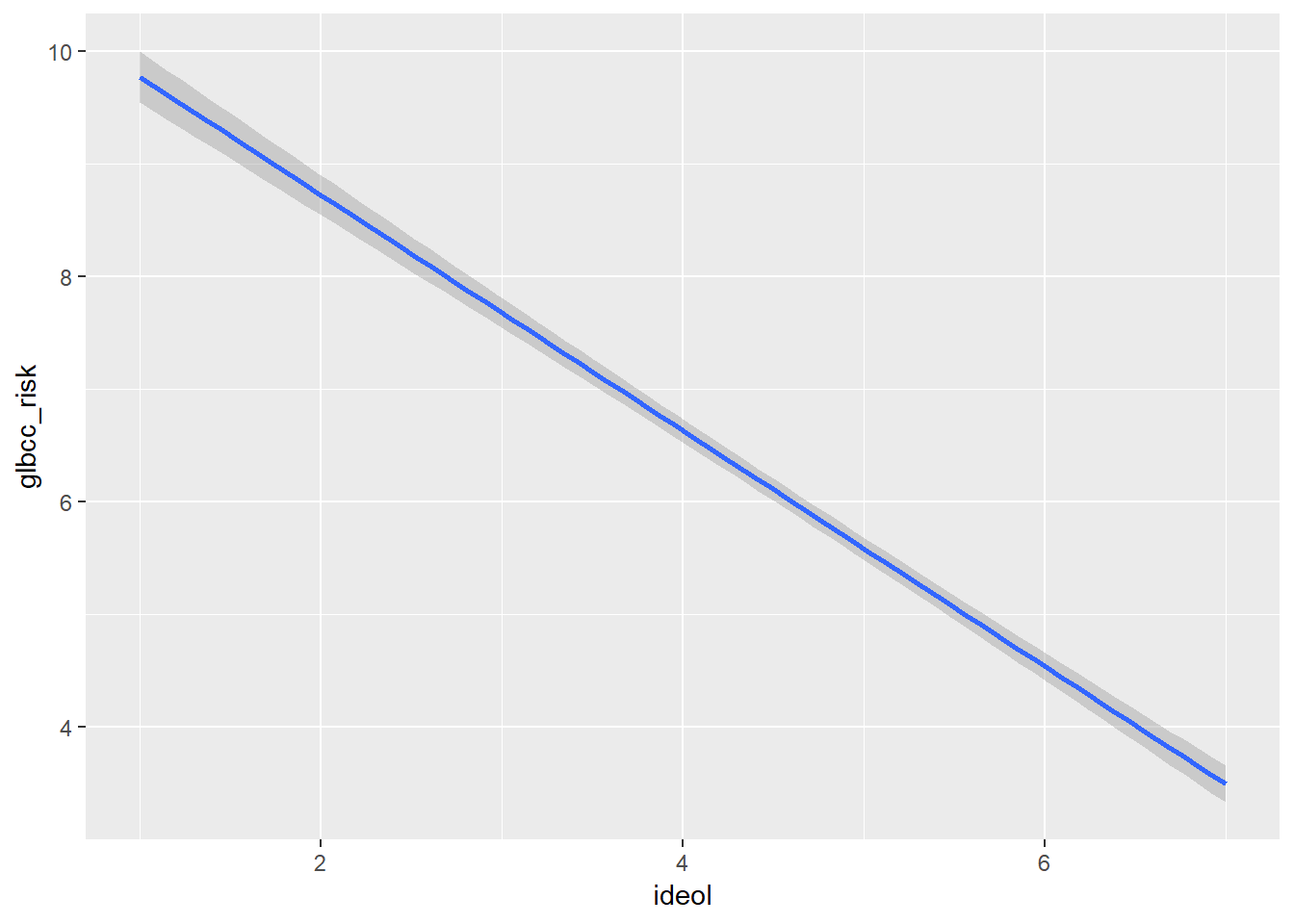
Limpieza del entorno R
Si recuerdas, al inicio del capítulo, creamos varios conjuntos de datos temporales. Deberíamos tomarnos el tiempo para aclarar nuestro espacio de trabajo para el próximo capítulo. La función rm en R los eliminará por nosotros.
rm(ds.omit) 

