4.13: Estimación de parámetros poblacionales

Hagamos una pausa por un momento para dirigirnos. Estamos a punto de entrar en el tema de la estimación. ¿Qué es eso y por qué debería importarte? En primer lugar, los parámetros poblacionales son cosas acerca de una distribución. Por ejemplo, las distribuciones tienen medios. La media es un parámetro de la distribución. La desviación estándar de una distribución es un parámetro. Cualquier cosa que pueda describir una distribución es un parámetro potencial.

Bien bien, ¿a quién le importa? Esta creo, es una muy buena pregunta. Hay algunas buenas razones concretas para cuidar. Y hay algunas grandes razones abstractas para cuidar. Desafortunadamente, la mayor parte del tiempo en la investigación, son las razones abstractas las que más importan, y estas pueden ser las más difíciles de entender.

 

Parámetros poblacionales concretos

Primero algunas razones concretas. Hay poblaciones reales por ahí, y a veces se quiere conocer los parámetros de las mismas. Por ejemplo, si eres una empresa de calzado, te gustaría conocer los parámetros poblacionales del tamaño de los pies. Como primer paso, querrías conocer la media y desviación estándar de la población. Si tu empresa supiera esto, y otras empresas no, a tu empresa le iría mejor (asumiendo que todos los zapatos son iguales). ¿Por qué le iría mejor a tu empresa y cómo podría usar los parámetros? Aquí hay una buena razón. Como empresa de calzado quieres satisfacer la demanda con la cantidad correcta de oferta. Si haces demasiados zapatos grandes o pequeños, y no hay suficiente gente para comprarlos, entonces estás haciendo zapatos extra que no venden. Si no haces lo suficiente de las tallas más populares, estarás dejando dinero en la mesa. ¿Correcto? Sí. Entonces, ¿qué sería lo óptimo para hacer? Quizás, harías diferentes cantidades de zapatos en cada talla, correspondientes a cómo la demanda de cada talla de zapato. Se sabría algo sobre la demanda averiguando la frecuencia de cada tamaño en la población. Se necesitaría conocer los parámetros poblacionales para hacer esto.

Afortunadamente, es bastante fácil obtener los parámetros poblacionales sin medir toda la población. ¿Quién tiene tiempo para medir los pies de todos los cuerpos? Nadie, ese es quién. En cambio, solo necesitarías elegir aleatoriamente a un grupo de personas, medir sus pies y luego medir los parámetros de la muestra. Si se toma una muestra lo suficientemente grande, hemos aprendido que la media muestral da una muy buena estimación de la media poblacional. En breve aprenderemos que una versión de la desviación estándar de la muestra también da una buena estimación de la desviación estándar de la población. Quizás los tamaños de zapatos tengan una forma ligeramente diferente a una distribución normal. Aquí también, si recolectas una muestra lo suficientemente grande, la forma de la distribución de la muestra será una buena estimación de la forma de las poblaciones. Todas estas son buenas razones para preocuparnos por estimar los parámetros poblacionales. Pero, ¿dirige una compañía de zapatos? Probablemente no.

 

Resumen de parámetros poblacionales

Incluso cuando pensamos que estamos hablando de algo concreto en Psicología, a menudo se vuelve abstracto de inmediato. En lugar de medir la población de tamaños de pies, ¿qué tal la población de felicidad humana? Todos pensamos que sabemos lo que es la felicidad, cada uno tiene más o menos de ella, hay un montón de gente, entonces debe haber una población de felicidad ¿verdad? Quizás, pero no es muy concreto. El primer problema es averiguar cómo medir la felicidad. Usemos un cuestionario. Considera estas preguntas:

¿Qué tan feliz estás ahora mismo en una escala del 1 al 7? ¿Qué tan feliz eres en general en una escala del 1 al 7? ¿Qué tan feliz eres por las mañanas en una escala del 1 al 7? ¿Qué tan feliz estás por las tardes en una escala del 1 al 7?

1. = muy infeliz
2. = infeliz
3. = una especie de infeliz
4. = en el medio
5. = una especie de feliz
6. = feliz
7. = muy feliz

Olvídate de hacer estas preguntas a todos en el mundo. Pidámoslos a mucha gente (nuestra muestra). ¿Qué crees que pasaría? Bueno, obviamente la gente daría bien todo tipo de respuestas. Podríamos contar las respuestas y trazarlas en un histograma. Esto nos mostraría una distribución de las puntuaciones de felicidad de nuestra muestra. “¡Genial, fantástico!” , usted dice. Sí, bien y dandy.

Entonces, por un lado podríamos decir muchas cosas sobre las personas de nuestra muestra. Podríamos decir exactamente quién dice que son felices y quién dice que no lo son, después de todo ¡nos acaban de decir!

Pero, ¿qué podemos decir de la población más grande? Podemos usar los parámetros de nuestra muestra (por ejemplo, media, desviación estándar, forma, etc.) para estimar algo sobre una población mayor. ¿Podemos inferir lo felices que están todos los demás, solo de nuestra muestra? SOSTENGA EL TELÉFONO.

 

Complicaciones con inferencia

Antes de enumerar un montón de complicaciones, déjame decirte qué creo que podemos hacer con nuestra muestra. Siempre que sea lo suficientemente grande, nuestros parámetros de muestra serán una estimación bastante buena de cómo sería otra muestra. Debido a la siguiente discusión, esto es a menudo todo lo que podemos decir. Pero, eso está bien, como ves a lo largo de este libro, ¡podemos trabajar con eso!

Problema 1: Múltiples poblaciones: Si observaste una gran muestra de datos del cuestionario encontrarás evidencia de múltiples distribuciones dentro de tu muestra. La gente responde las preguntas de manera diferente. Algunas personas son muy cautelosas y no muy extremas. Sus respuestas tenderán a distribuirse alrededor de la mitad de la escala, en su mayoría 3s, 4s y 5s. Algunas personas son muy bimodales, son muy felices y muy infelices, dependiendo de la hora del día. Las respuestas de estas personas serán en su mayoría 1s y 2s, y 6s y 7s, y esos números parecen provenir de una distribución completamente diferente. Algunas personas son completamente felices o completamente infelices. Nuevamente, estas dos “poblaciones” de números de personas parecen dos distribuciones diferentes, una con mayormente 6s y 7s, y otra con mayormente 1s y 2s. Otras personas serán más aleatorias, y sus puntajes se verán como una distribución uniforme. Entonces, ¿hay una sola población con parámetros que podamos estimar a partir de nuestra muestra? Probablemente no. Podría ser una mezcla de lotes de poblaciones con diferentes distribuciones.

Problema 2: ¿Qué miden estas preguntas? : Si el objetivo de hacer el cuestionario es estimar la felicidad de la población, realmente necesitamos preguntarnos si las mediciones de la muestra realmente nos dicen algo sobre la felicidad en primer lugar. Algunas preguntas: ¿Las personas son acertadas al decir lo felices que son? ¿La medida de la felicidad depende de la escala, por ejemplo, los resultados serían diferentes si usáramos 0-100, o -100 a +100, o no números? ¿La medida de la felicidad depende de la redacción de la pregunta? ¿Una medida como esta nos dice todo lo que queremos saber sobre la felicidad (probablemente no), qué le falta (quién sabe? probablemente muchos). En definitiva, nadie sabe si este tipo de preguntas miden lo que queremos que midan. Sólo esperamos que lo hagan. En cambio, tenemos una muy buena idea del tipo de cosas que realmente miden. Es realmente bastante obvio, y mirándote a la cara. Las mediciones del cuestionario miden cómo las personas responden a los cuestionarios. En otras palabras, cómo se comportan las personas y responden preguntas cuando se les da un cuestionario. Esto también podría medir algo sobre la felicidad, cuando la pregunta tiene que ver con la felicidad. Pero, resulta que las personas son notablemente consistentes en cómo responden preguntas, incluso cuando las preguntas son tonterías totales, o no tienen preguntas en absoluto (¡solo números para elegir!) Maul (2017).

Las complicaciones para llevar a casa aquí son que podemos recolectar muestras, pero en Psicología, muchas veces no tenemos una buena idea de las poblaciones que podrían estar vinculadas a estas muestras. Puede haber muchas poblaciones, o las poblaciones podrían ser diferentes dependiendo de a quién le preguntes. Por último, la “población” podría no ser la que tú quieres que sea.

 

Experimentos y parámetros poblacionales

Bien, entonces no somos dueños de una compañía de zapatos, y realmente no podemos identificar a la población de interés en Psicología, ¿no podemos simplemente saltarnos esta sección en estimación? Después de todo, la “población” es simplemente demasiado extraña y abstracta e inútil y contenciosa. ¡SOSTENGA EL TELÉFONO OTRA VEZ!

Resulta que podemos aplicar las cosas que hemos estado aprendiendo para resolver muchos problemas importantes en la investigación. Estos nos permiten responder preguntas con los datos que recopilamos. La estimación de parámetros es una de estas herramientas. Solo necesitamos ser un poco más creativos, y un poco más abstractos para usar las herramientas.

Esto es lo que ya sabemos. Los números que medimos vienen de alguna parte, hemos llamado a este lugar “distribuciones”. Las distribuciones controlan cómo llegan los números. Algunos números ocurren más que otros dependiendo de la distribución. Asumimos, aunque no sepamos cuál es la distribución, o lo que significa, que los números vinieron de uno. Segundo, cuando conseguimos algunos números, lo llamamos muestra. Todo este capítulo hasta el momento te ha enseñado una cosa. Cuando tu muestra es grande, se asemeja a la distribución de la que proviene. Y, cuando tu muestra sea grande, se parecerá muy de cerca a cómo se verá otra gran muestra de lo mismo. ¡Podemos usar este conocimiento!

Muy a menudo como Psicólogos lo que queremos saber es qué causa qué. Queremos saber si X provoca que algo cambie en Y. ¿Comer chocolate te hace más feliz? ¿Estudiar mejora tus calificaciones? Ahí hay un bazillions de este tipo de preguntas. Y, queremos respuestas a ellos.

He estado tratando de ser mayormente concreto hasta el momento en este libro de texto, por eso hablamos de tonterías como el chocolate y la felicidad, al menos son concretas. Vamos a darle una oportunidad a ser abstracto. Podemos hacerlo.

Entonces, queremos saber si X hace que Y cambie. ¿Qué es X? ¿Qué es Y? X es algo que cambias, algo que manipulas, la variable independiente. Y es algo que se mide. Entonces, estaremos tomando muestras de Y. “Oh, lo pillo, tomaremos muestras de Y, entonces podremos usar los parámetros muestrales para estimar los parámetros poblacionales de Y!” NO, en realidad no, pero sí algo así. Tomaremos muestra de Y, eso es algo que absolutamente hacemos. De hecho, eso es realmente todo lo que hacemos alguna vez, razón por la cual hablar de la población de Y no tiene sentido. Estamos más interesados en nuestras muestras de Y, y cómo se comportan.

Entonces, qué pasaría si elimináramos a X del universo por completo, y luego tomáramos una gran muestra de Y. Vamos a fingir que Y mide algo en un experimento de Psicología. Entonces, sabemos de inmediato que Y es variable. Cuando tomamos una muestra grande, tendrá una distribución (porque Y es variable). Entonces, podemos hacer cosas como medir la media de Y, y medir la desviación estándar de Y, y cualquier otra cosa que queramos saber sobre Y. Bien. Qué pasaría si replicáramos esta medición. Es decir, solo tomamos otra muestra aleatoria de Y, tan grande como la primera. Lo que debería suceder es que nuestra primera muestra debería parecerse mucho a nuestro segundo ejemplo. Después de todo, no le hicimos nada a Y, solo tomamos dos muestras grandes dos veces. Ambas muestras serán un poco diferentes (debido al error de muestreo), pero en su mayoría serán las mismas. Cuanto más grandes sean nuestras muestras, más se verán iguales, sobre todo cuando no hacemos nada para hacer que sean diferentes. Es decir, podemos usar los parámetros de una muestra para estimar los parámetros de una segunda muestra, porque tenderán a ser los mismos, especialmente cuando son grandes.

Ya estamos listos para el paso dos. Quieres saber si X cambia Y. ¿Qué haces? Haces que X suba y tomes una gran muestra de Y luego mírala. Haces que X baje, luego toma una segunda gran muestra de Y y mírala. A continuación, compara las dos muestras de Y. Si X no hace nada entonces ¿qué deberías encontrar? Ya lo discutimos en el párrafo anterior. Si X no hace nada, entonces tus dos grandes muestras de Y deberían ser bastante similares. No obstante, si X le hace algo a Y, entonces una de sus grandes muestras de Y será diferente a la otra. Habrás cambiado algo de Y. Quizás X hace que la media de Y cambie. O tal vez X hace que la variación en Y cambie. O, tal vez X haga cambiar toda la forma de la distribución. Si encontramos algún cambio grande que no pueda explicarse por el error de muestreo, entonces podemos concluir que algo sobre X causó un cambio en Y! ¡Podríamos usar este enfoque para conocer qué causa qué!

La idea muy importante sigue siendo sobre la estimación, solo que no la estimación de parámetros de población exactamente. Sabemos que cuando tomamos muestras varían naturalmente. Entonces, cuando estimamos un parámetro de una muestra, como la media, sabemos que estamos fuera por alguna cantidad. Cuando encontramos que dos muestras son diferentes, necesitamos averiguar si el tamaño de la diferencia es consistente con lo que el error de muestreo puede producir, o si la diferencia es mayor que eso. Si la diferencia es mayor, entonces podemos estar seguros de que el error de muestreo no produjo la diferencia. Entonces, podemos inferir con confianza que algo más (como una X) sí causó la diferencia. Este poco de pensamiento abstracto es de lo que trata la mayor parte del resto del libro de texto. Determinar si hay alguna diferencia causada por tu manipulación. Hay más en la historia, siempre hay. Podemos ser más específicos que solo, hay alguna diferencia, pero con fines introductorios, nos centraremos en la búsqueda de diferencias como concepto fundacional.

 

Resumen provisional

Hemos hablado de estimación sin hacer ninguna estimación, por lo que en la siguiente sección haremos alguna estimación de la media y de la desviación estándar. Formalmente, hablamos de esto como usar una muestra para estimar un parámetro de la población. Siéntase libre de pensar en la “población” de diferentes maneras. Podría ser población concreta, como la distribución de tamaños de pies. O bien, podría ser algo más abstracto, como la estimación de parámetros de cómo suelen verse las muestras cuando provienen de una distribución.

 

Estimación de la media poblacional

Supongamos que vamos a Brooklyn y 100 de los lugareños tienen la amabilidad de pasar por una prueba de coeficiente intelectual. El puntaje promedio de CI entre estas personas resulta ser\(\bar{X}=98.5\). Entonces, ¿cuál es el verdadero coeficiente intelectual medio para toda la población de Brooklyn? Obviamente, no sabemos la respuesta a esa pregunta. Podría ser\(97.2\), pero si también podría ser\(103.5\). Nuestro muestreo no es exhaustivo por lo que no podemos dar una respuesta definitiva. Sin embargo si se ve obligado a dar una “mejor suposición” tendría que decir\(98.5\). Esa es la esencia de la estimación estadística: dar una mejor suposición. Estamos usando la media de la muestra como la mejor estimación de la media poblacional.

En este ejemplo, estimar el parámetro de población desconocido es sencillo. Calculo la media muestral, y la uso como mi estimación de la media poblacional. Es bastante simple, y en la siguiente sección explicaremos la justificación estadística de esta respuesta intuitiva. No obstante, por el momento vamos a asegurarnos de reconocer que el estadístico muestral y la estimación del parámetro poblacional son cosas conceptualmente diferentes. Un estadístico de muestra es una descripción de sus datos, mientras que la estimación es una suposición sobre la población. Con eso en mente, los estadísticos suelen utilizar notación diferente para referirse a ellos. Por ejemplo, si se denota la verdadera media poblacional\(\mu\), entonces usaríamos\(\hat\mu\) para referirnos a nuestra estimación de la media poblacional. En contraste, la media muestral se denota\(\bar{X}\) o a veces\(m\). Sin embargo, en muestras simples al azar, la estimación de la media poblacional es idéntica a la media muestral: si observo una media muestral de\(\bar{X} = 98.5\), entonces mi estimación de la media poblacional también lo es\(\hat\mu = 98.5\). Para ayudar a mantener la notación clara, aquí hay una tabla práctica:

Símbolo	¿Qué es?	¿Sabemos lo que es?
\(\bar{X}\)	Media de la muestra	Sí, calculado a partir de los datos brutos
\(\mu\)	Media verdadera de la población	Casi nunca se sabe con certeza
\(\hat{\mu}\)	Estimación de la media poblacional	Sí, idéntica a la media de la muestra

 

Estimación de la desviación estándar de la población

Hasta ahora, la estimación parece bastante simple, y tal vez te estés preguntando por qué te obligué a leer todas esas cosas sobre la teoría del muestreo. En el caso de la media, nuestra estimación del parámetro poblacional (i.e.\(\hat\mu\)) resultó ser idéntica a la estadística muestral correspondiente (i.e.\(\bar{X}\)). Sin embargo, eso no siempre es cierto. Para ver esto, pensemos cómo construir una estimación de la desviación estándar de la población, que vamos a denotar\(\hat\sigma\). ¿Cuál vamos a utilizar como estimación en este caso? Tu primer pensamiento podría ser que podríamos hacer lo mismo que hicimos al estimar la media, y simplemente usar el estadístico de muestra como nuestra estimación. Eso es casi lo correcto, pero no del todo.

He aquí por qué. Supongamos que tengo una muestra que contiene una sola observación. Para este ejemplo, ayuda considerar una muestra donde no tienes intuiciones en absoluto sobre cuáles podrían ser los verdaderos valores de la población, así que usemos algo completamente ficticio. Supongamos que la observación en cuestión mide la cromulencia de mis zapatos. Resulta que mis zapatos tienen una cromulencia de 20. Así que aquí está mi muestra:

20

Esta es una muestra perfectamente legítima, incluso si tiene un tamaño de muestra de\(N=1\). Tiene una media muestral de 20, y porque cada observación en esta muestra es igual a la media muestral (¡obviamente!) tiene una desviación estándar muestral de 0. Como descripción de la muestra esto parece bastante correcto: la muestra contiene una sola observación y por lo tanto no se observa variación dentro de la muestra. Una desviación estándar de muestra\(s = 0\) es la respuesta correcta aquí. Pero como estimación de la desviación estándar de la población, se siente completamente demente, ¿verdad? Es cierto que tú y yo no sabemos nada sobre lo que es la “cromulencia”, pero sabemos algo sobre los datos: ¡la única razón por la que no vemos ninguna variabilidad en la muestra es que la muestra es demasiado pequeña para mostrar alguna variación! Entonces, si tienes un tamaño de muestra de\(N=1\), parece que la respuesta correcta es solo decir “ni idea en absoluto”.

Observe que no tiene la misma intuición cuando se trata de la media muestral y la media poblacional. Si se ve obligado a hacer una mejor conjetura sobre la media poblacional, no se siente completamente demente adivinar que la media poblacional es 20. Seguro, probablemente no te sentirías muy confiado en esa suposición, porque solo tienes la única observación con la que trabajar, pero sigue siendo la mejor conjetura que puedes hacer.

Extendamos un poco este ejemplo. Supongamos que ahora hago una segunda observación. Mi conjunto de datos ahora tiene\(N=2\) observaciones de la cromulencia de los zapatos, y la muestra completa ahora se ve así:

20, 22

En esta ocasión, nuestra muestra es lo suficientemente grande como para que podamos observar alguna variabilidad: ¡dos observaciones es el número mínimo necesario para que se observe cualquier variabilidad! Para nuestro nuevo conjunto de datos, la media de la muestra es\(\bar{X}=21\), y la desviación estándar de la muestra es\(s=1\). ¿Qué intuiciones tenemos sobre la población? Nuevamente, en lo que respecta a la media poblacional, la mejor conjetura que podemos hacer es la media muestral: si se obliga a adivinar, probablemente adivinaríamos que la cromulencia media poblacional es 21. ¿Qué pasa con la desviación estándar? Esto es un poco más complicado. La desviación estándar de la muestra se basa únicamente en dos observaciones, y si eres como yo probablemente tengas la intuición de que, con solo dos observaciones, no le hemos dado a la población “suficientes oportunidades” para revelarnos su verdadera variabilidad. No es sólo que sospechemos que la estimación es incorrecta: después de todo, con sólo dos observaciones esperamos que esté equivocada hasta cierto punto. La preocupación es que el error sea sistemático.

Si el error es sistemático, eso significa que está sesgado. Por ejemplo, imagínese si la media muestral fue siempre menor que la media poblacional. Si esto fuera cierto (no lo es), entonces no podríamos usar la media de la muestra como estimador. Sería sesgado, estaríamos usando el número equivocado.

Resulta que la desviación estándar de la muestra es un estimador sesgado de la desviación estándar de la población. Podemos anticiparnos a esto por lo que hemos estado discutiendo. Cuando el tamaño de la muestra es 1, la desviación estándar es 0, que obviamente es pequeña. Cuando el tamaño de la muestra es 2, la desviación estándar se convierte en un número mayor que 0, pero debido a que solo tenemos dos muestras, sospechamos que aún podría ser demasiado pequeña. Resulta que esta intuición es correcta.

Sería bueno demostrar esto de alguna manera. De hecho hay pruebas matemáticas que confirman esta intuición, pero a menos que tengas los antecedentes matemáticos adecuados no ayudan mucho. En cambio, lo que voy a hacer es usar R para simular los resultados de algunos experimentos. Con eso en mente, volvamos a nuestros estudios de CI. Supongamos que el coeficiente intelectual medio poblacional verdadero es 100 y la desviación estándar es 15. Puedo usar la función rnorm () para generar los resultados de un experimento en el que mido puntajes de\(N=2\) CI, y calcular la desviación estándar de la muestra. Si hago esto una y otra vez, y trazo un histograma de estas desviaciones estándar de muestra, lo que tengo es la distribución muestral de la desviación estándar. He trazado esta distribución en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Distribución muestral de la desviación estándar de la muestra para un experimento de dos puntajes de CI. La verdadera desviación estándar de la población es de 15 (línea discontinua), pero como se puede ver en el histograma, la gran mayoría de los experimentos producirán una desviación estándar de la muestra mucho más pequeña que esta. En promedio, este experimento produciría una desviación estándar muestral de sólo 8.5, ¡muy por debajo del valor verdadero! En otras palabras, la desviación estándar de la muestra es una estimación sesgada de la desviación estándar de la población.

A pesar de que la verdadera desviación estándar de la población es de 15, el promedio de las desviaciones estándar de la muestra es de sólo 8.5. Observe que esto es muy diferente de cuando estábamos trazando distribuciones de muestreo de la media muestral, las que siempre estuvieron centradas alrededor de la media de la población.

Ahora vamos a extender la simulación. En lugar de restringirnos a la situación en la que tenemos un tamaño de muestra de\(N=2\), repitamos el ejercicio para tamaños de muestra del 1 al 10. Si trazamos la media de la muestra promedio y la desviación estándar promedio de la muestra en función del tamaño de la muestra, se obtienen los siguientes resultados.

La figura\(\PageIndex{2}\) muestra la media de la muestra en función del tamaño de la muestra. Observe que es una línea plana. La media muestral no subestima ni sobreestima la media poblacional. ¡Es una estimación imparcial!

Figura\(\PageIndex{2}\): Una ilustración del hecho de que la media muestral es un estimador imparcial de la media poblacional.

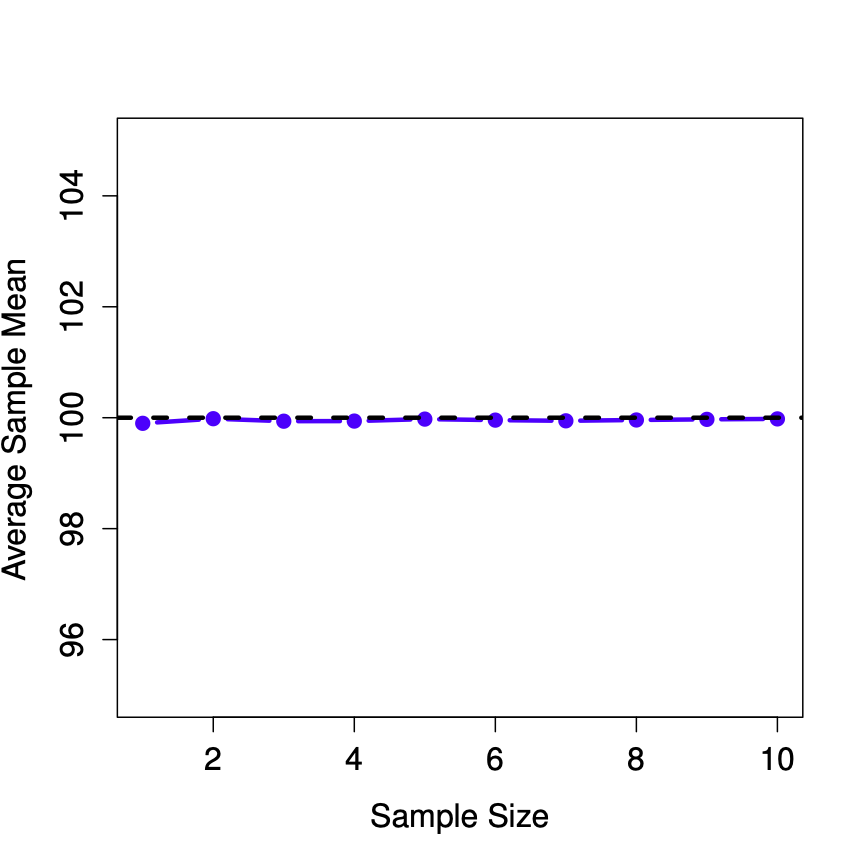
La figura\(\PageIndex{3}\) muestra la desviación estándar de la muestra en función del tamaño de la muestra. Observe que no es una línea plana. ¡La desviación estándar de la muestra subestima sistemáticamente la desviación estándar de la población!

Figura\(\PageIndex{3}\): Una ilustración del hecho de que la desviación estándar de la muestra es un estimador sesgado de la desviación estándar de la población.

En otras palabras, si queremos hacer una “mejor conjetura” (\(\hat\sigma\), nuestra estimación de la desviación estándar de la población) sobre el valor de la desviación estándar de la población\(\sigma\), debemos asegurarnos de que nuestra conjetura sea un poco mayor que la desviación estándar de la muestra\(s\).

La solución a este sesgo sistemático resulta muy simple. Así es como funciona. Antes de abordar la desviación estándar, veamos la varianza. Si recuerda del segundo capítulo, la varianza de la muestra se define como el promedio de las desviaciones cuadradas de la media de la muestra. Es decir:

\[s^2 = \frac{1}{N} \sum_{i=1}^N (X_i - \bar{X})^2 \nonumber \]

La varianza muestral\(s^2\) es un estimador sesgado de la varianza poblacional\(\sigma^2\). Pero resulta que solo necesitamos hacer un pequeño retoque para transformar esto en un estimador imparcial. Todo lo que tenemos que hacer es dividir por\(N-1\) más que por\(N\). Si hacemos eso, obtenemos la siguiente fórmula:

\[\hat\sigma^2 = \frac{1}{N-1} \sum_{i=1}^N (X_i - \bar{X})^2 \nonumber \]

Se trata de un estimador imparcial de la varianza poblacional\(\sigma\).

Una historia similar se aplica para la desviación estándar. Si dividimos por\(N-1\) más que\(N\), nuestra estimación de la desviación estándar de la población se convierte en:

\[\hat\sigma = \sqrt{\frac{1}{N-1} \sum_{i=1}^N (X_i - \bar{X})^2} \nonumber \]

Vale la pena señalar que los programas de software hacen suposiciones por ti, sobre qué varianza y desviación estándar estás calculando. Algunos programas se dividen automáticamente por\(N-1\), otros no. Es necesario verificar para averiguar qué están haciendo. No dejes que el software te diga qué hacer. El software es para que usted le diga qué hacer.

Un punto final: en la práctica, mucha gente tiende a referirse a\(\hat{\sigma}\) (es decir, la fórmula donde dividimos por\(N-1\)) como la desviación estándar de la muestra. Técnicamente, esto es incorrecto: la desviación estándar de la muestra debe ser igual a\(s\) (es decir, la fórmula donde dividimos por\(N\)). No son lo mismo, ni conceptual ni numéricamente. Una es propiedad de la muestra, la otra es una característica estimada de la población. Sin embargo, en casi todas las aplicaciones de la vida real, lo que realmente nos importa es la estimación del parámetro poblacional, y así la gente siempre informa\(\hat\sigma\) más que\(s\).

Nota

Tenga en cuenta que si debe dividir por N o N-1 también depende de su filosofía sobre lo que esté haciendo. Por ejemplo, si no crees que lo que estás haciendo es estimar un parámetro de población, entonces ¿por qué dividirías por N-1? Además, cuando N es grande, no importa demasiado. La diferencia entre un N grande, y un N-1 grande, es apenas -1.

Este es el número correcto para reportar, por supuesto, es que las personas tienden a ponerse un poco imprecisas sobre la terminología cuando la escriben, porque la “desviación estándar de la muestra” es más corta que la “desviación estándar estimada de la población”. No es gran cosa, y en la práctica hago lo mismo que hacen todos los demás. No obstante, creo que es importante mantener separados los dos conceptos: nunca es buena idea confundir “propiedades conocidas de tu muestra” con “conjeturas sobre la población de la que procede”. En el momento en que empiezas a pensar eso\(s\) y\(\hat\sigma\) eres lo mismo, empiezas a hacer exactamente eso.

Para terminar esta sección, aquí hay otro par de tablas para ayudar a mantener las cosas claras:

Símbolo	¿Qué es?	¿Sabemos lo que es?
\(s^2\)	Varianza de la muestra	Sí, calculado a partir de los datos brutos
\(\sigma^2\)	Varianza poblacional	Casi nunca se sabe con certeza
\(\hat{\sigma}^2\)	Estimación de la varianza poblacional	Sí, pero no lo mismo que la varianza de la muestra