8.3: Cálculo del ANOVA de RM

Ahora que estás familiarizado con el concepto de una tabla ANOVA (¿recuerdas la tabla del último capítulo donde reportamos todas las partes para calcular el\(F\) -valor?) , podemos echar un vistazo a las cosas que necesitamos averiguar para hacer la tabla ANOVA. La siguiente figura presenta un resumen para la tabla ANOVA de medidas repetidas. Nos muestra todo lo que necesitamos calcular para obtener el\(F\) -valor de nuestros datos.

Figura\(\PageIndex{1}\): Ecuaciones para el cálculo de la tabla ANOVA para un diseño de medidas repetidas.

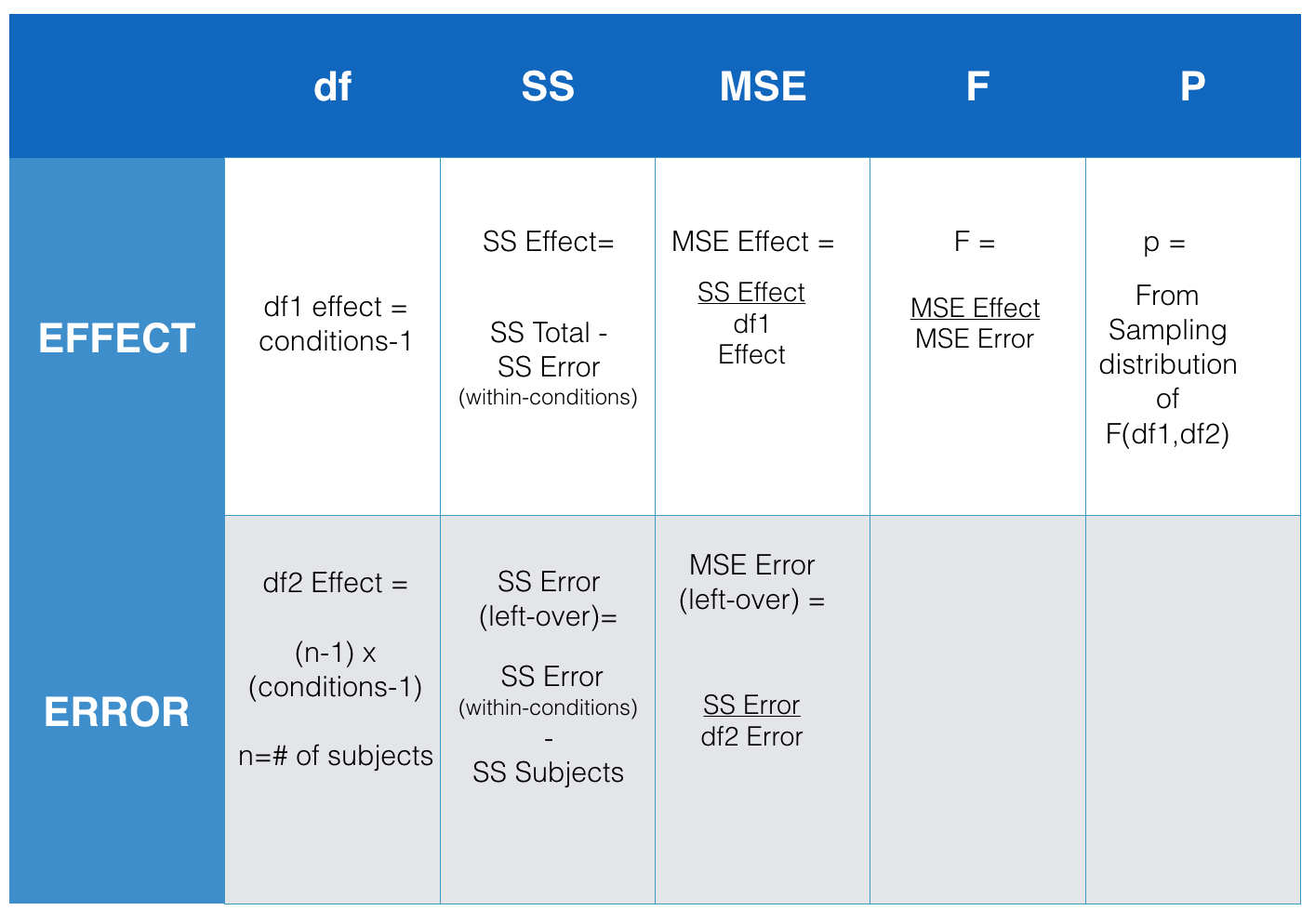
Entonces, lo que tenemos que hacer es calcular todas las\(SS\) es que hicimos antes para el ANOVA entre sujetos. Eso significa que los siguientes tres pasos son idénticos a los que hiciste antes. De hecho, básicamente voy a copiar los siguientes tres pasos para encontrar\(SS_\text{TOTAL}\),\(SS_\text{Effect}\), y\(SS_\text{Error (within-conditions)}\). Después de eso hablaremos de\(SS_\text{Error (within-conditions)}\) dividirnos en dos partes, esto es lo nuevo para este capítulo. ¡Aquí vamos!

 

SS Total

Las sumas totales de cuadrados, o\(SS\text{Total}\) mide la variación total en un conjunto de datos. Todo lo que hacemos es encontrar la diferencia entre cada puntaje y la gran media, luego cuadramos las diferencias y las sumamos todas.

suppressPackageStartupMessages(library(dplyr))
scores <- c(20,11,2,6,2,7,2,11,2)
conditions <- as.character(rep(c("A","B","C"), each=3))
subjects <-rep(1:3,3)
diff <-scores-mean(scores)
diff_squared <-diff^2
df<-data.frame(subjects,conditions,scores,diff, diff_squared)
df$conditions<-as.character(df$conditions)
df$subjects<-as.character(df$subjects)
df <- df %>%
  rbind(c("Sums","", colSums(df[1:9,3:5]))) %>%
  rbind(c("Means","",colMeans(df[1:9,3:5])))
knitr::kable(df)

asignaturas	condiciones	puntuaciones	diff	diff_squared
1	A	20	13	169
2	A	11	4	16
3	A	2	-5	25
1	B	6	-1	1
2	B	2	-5	25
3	B	7	0	0
1	C	2	-5	25
2	C	11	4	16
3	C	2	-5	25
Sumas		63	0	302
Medios		7	0	33.55555555556

La media de todas las puntuaciones se llama la Gran Media. Se calcula en la tabla, la Gran Media = 7.

También calculamos todas las puntuaciones de diferencia a partir de la Gran Media. Las puntuaciones de diferencia están en la columna titulada diff. A continuación, cuadramos las puntuaciones de diferencia, y esas están en la siguiente columna llamada diff_squared.

Cuando sumas todas las desviaciones cuadradas individuales (sscores de diferencia) obtienes las sumas de cuadrados. Por eso se llama las sumas de cuadrados (SS).

Ahora, tenemos la primera parte de nuestra respuesta:

\[SS_\text{total} = SS_\text{Effect} + SS_\text{Error} \nonumber \]

\[SS_\text{total} = 302 \nonumber \]

y

\[302 = SS_\text{Effect} + SS_\text{Error} \nonumber \]

 

Efecto SS

\(SS_\text{Total}\)nos dio un número que representa todo el cambio en nuestros datos, en qué se diferencian todos de la gran media.

Lo que queremos hacer a continuación es estimar cuánto del cambio total en los datos podría deberse a la manipulación experimental. Por ejemplo, si ejecutamos un experimento que provoca cambios en la medición, entonces las medias para cada grupo serán diferentes de las demás, y las puntuaciones en cada grupo serán diferentes de cada uno. Como resultado, las fuerzas de manipulación cambian sobre los números, y esto naturalmente significará que alguna parte de la variación total en los números es causada por la manipulación.

La manera de aislar la variación debido a la manipulación (también llamada efecto) es mirar las medias en cada grupo, y calcular las puntuaciones de diferencia entre la media de cada grupo y la media grande, y luego las desviaciones cuadradas para encontrar la suma para\(SS_\text{Effect}\).

Considera esta tabla, mostrando los cálculos para\(SS_\text{Effect}\).

suppressPackageStartupMessages(library(dplyr))
scores <- c(20,11,2,6,2,7,2,11,2)
conditions <- as.character(rep(c("A","B","C"), each=3))
subjects <-rep(1:3,3)
means <-c(11,11,11,5,5,5,5,5,5)
diff <-means-mean(scores)
diff_squared <-diff^2
df<-data.frame(subjects,conditions,scores,means,diff, diff_squared)
df$conditions<-as.character(df$conditions)
df$subjects<-as.character(df$subjects)
df <- df %>%
  rbind(c("Sums","", colSums(df[1:9,3:6]))) %>%
  rbind(c("Means","",colMeans(df[1:9,3:6])))
knitr::kable(df)

asignaturas	condiciones	puntuaciones	significa	diff	diff_squared
1	A	20	11	4	16
2	A	11	11	4	16
3	A	2	11	4	16
1	B	6	5	-2	4
2	B	2	5	-2	4
3	B	7	5	-2	4
1	C	2	5	-2	4
2	C	11	5	-2	4
3	C	2	5	-2	4
Sumas		63	63	0	72
Medios		7	7	0	8

Observe que creamos una nueva columna llamada media, estas son las medias para cada condición, A, B y C.

\(SS_\text{Effect}\)representa la cantidad de variación que es causada por diferencias entre las medias. La columna diff es la diferencia entre cada media de condición y la gran media, así que para la primera fila, tenemos 11-7 = 4, y así sucesivamente.

Encontramos que\(SS_\text{Effect} = 72\), esto es lo mismo que el ANOVA del capítulo anterior

 

Error SS (dentro de las condiciones)

Genial, llegamos a SS Error. Ya encontramos SS Total, y SS Effect, así que ahora podemos resolver para SS Error así:

\[SS_\text{total} = SS_\text{Effect} + SS_\text{Error (within-conditions)} \nonumber \]

conmutación alrededor:

\[ SS_\text{Error} = SS_\text{total} - SS_\text{Effect} \nonumber \]

\[ SS_\text{Error (within conditions)} = 302 - 72 = 230 \nonumber \]

O bien, podríamos calcular\(SS_\text{Error (within conditions)}\) directamente a partir de los datos como lo hicimos la última vez:

suppressPackageStartupMessages(library(dplyr))
scores <- c(20,11,2,6,2,7,2,11,2)
conditions <- as.character(rep(c("A","B","C"), each=3))
subjects <-rep(1:3,3)
means <-c(11,11,11,5,5,5,5,5,5)
diff <-means-scores
diff_squared <-diff^2
df<-data.frame(subjects,conditions,scores,means,diff, diff_squared)
df$conditions<-as.character(df$conditions)
df$subjects<-as.character(df$subjects)
df <- df %>%
  rbind(c("Sums","", colSums(df[1:9,3:6]))) %>%
  rbind(c("Means","",colMeans(df[1:9,3:6])))
knitr::kable(df)

asignaturas	condiciones	puntuaciones	significa	diff	diff_squared
1	A	20	11	-9	81
2	A	11	11	0	0
3	A	2	11	9	81
1	B	6	5	-1	1
2	B	2	5	3	9
3	B	7	5	-2	4
1	C	2	5	3	9
2	C	11	5	-6	36
3	C	2	5	3	9
Sumas		63	63	0	230
Medios		7	7	0	25.55555555556

Cuando calculamos\(SS_\text{Error (within conditions)}\) directamente, encontramos la diferencia entre cada puntaje y la condición media para esa puntuación. Esto nos da la variación de error restante alrededor de la media de condición, que la media de condición no explica.

 

Sujetos SS

Ahora estamos listos para calcular nueva partición, llamada\(SS_\text{Subjects}\). Primero encontramos los medios para cada tema. Para el sujeto 1, esta es la media de sus puntuaciones en las Condiciones A, B y C. La media para el sujeto 1 es 9.33 (repitiendo). Observe que aquí va a haber algún error de redondeo, eso está bien por ahora.

La columna de medias muestra ahora todas las medias del sujeto. Luego encontramos la diferencia entre cada media de sujeto y la gran media. Estas desviaciones se muestran en la columna diff. Entonces cuadramos las desviaciones, y las resumimos.

suppressPackageStartupMessages(library(dplyr))
scores <- c(20,11,2,6,2,7,2,11,2)
conditions <- as.character(rep(c("A","B","C"), each=3))
subjects <-rep(1:3,3)
means <-c(9.33,8,3.66,9.33,8,3.66,9.33,8,3.66)
diff <-means-mean(scores)
diff_squared <-diff^2
df<-data.frame(subjects,conditions,scores,means,diff, diff_squared)
df$conditions<-as.character(df$conditions)
df$subjects<-as.character(df$subjects)
df <- df %>%
  rbind(c("Sums","", colSums(df[1:9,3:6]))) %>%
  rbind(c("Means","",colMeans(df[1:9,3:6])))
knitr::kable(df)

asignaturas	condiciones	puntuaciones	significa	diff	diff_squared
1	A	20	9.33	2.33	5.4289
2	A	11	8	1	1
3	A	2	3.66	-3.34	11.1556
1	B	6	9.33	2.33	5.4289
2	B	2	8	1	1
3	B	7	3.66	-3.34	11.1556
1	C	2	9.33	2.33	5.4289
2	C	11	8	1	1
3	C	2	3.66	-3.34	11.1556
Sumas		63	62.97	-0.02999999999994	52.7535
Medios		7	6.996666666667	-0.003333333333326	5.8615

Encontramos que la suma de las desviaciones cuadradas\(SS_\text{Subjects}\) = 52.75. Observe nuevamente, esto tiene algún pequeño error de redondeo debido a que algunas de las medias del sujeto tenían decimales repetidos, y no se dividieron de manera uniforme.

Podemos ver el efecto del error de redondeo si miramos la suma y la media en la columna diff. Sabemos que estos deben ser ambos cero, porque la Gran media es el punto de equilibrio en los datos. La suma y la media son ambas muy cercanas a cero, pero no son cero por error de redondeo.

 

Error SS (sobrante)

Ahora podemos hacer lo último. Recuerden que queríamos\(SS_\text{Error (within conditions)}\) dividir la en dos partes,\(SS_\text{Subjects}\) y\(SS_\text{Error (left-over)}\). Porque ya hemos calculado\(SS_\text{Error (within conditions)}\) y\(SS_\text{Subjects}\), podemos resolver para\(SS_\text{Error (left-over)}\):

\[SS_\text{Error (left-over)} = SS_\text{Error (within conditions)} - SS_\text{Subjects} \nonumber \]

\[SS_\text{Error (left-over)} = SS_\text{Error (within conditions)} - SS_\text{Subjects} = 230 - 52.75 = 177.25 \nonumber \]

 

Consulta nuestro trabajo

Antes de continuar calculando los MSE y el valor F para nuestros datos, verifiquemos rápidamente nuestro trabajo. Por ejemplo, podríamos hacer que R calcule el ANOVA de medidas repetidas para nosotros, y luego podríamos mirar la tabla ANOVA y ver si estamos en el camino correcto hasta el momento.

suppressPackageStartupMessages(library(dplyr))
library(xtable)
scores <- c(20,11,2,6,2,7,2,11,2)
conditions <- as.character(rep(c("A","B","C"), each=3))
subjects <-rep(1:3,3)
means <-c(9.33,8,3.66,9.33,8,3.66,9.33,8,3.66)
diff <-means-mean(scores)
diff_squared <-diff^2
df<-data.frame(subjects,conditions,scores,means,diff, diff_squared)
df$conditions<-as.character(df$conditions)
df$subjects<-as.character(df$subjects)

summary_out <- summary(aov(scores~conditions + Error(subjects/conditions),df[1:9,]))
knitr::kable(xtable(summary_out))

	Df	Suma Cuadrados	Media Cuadrada	Valor F	Pr (>F)
Residuales	2	52.66667	26.33333	NA	F)" style="vertical-align:middle;">NA
condiciones	2	72.00000	36.00000	0.8120301	F)" style="vertical-align:middle;">0.505848
Residuales	4	177.33333	44.33333	NA	F)" style="vertical-align:middle;">NA

Bien, se ve bien. Encontramos\(SS_\text{Effect}\) que el es 72, y el SS para las condiciones (lo mismo) en la tabla también es 72. Encontramos\(SS_\text{Subjects}\) que el es 52.75, y el SS para el primer residual (lo mismo) en la tabla también se repite 53.66. Eso está cerca, y nuestro número está apagado por error de redondeo. Por último, encontramos que el\(SS_\text{Error (left-over)}\) es 177.25, y el SS para los residuales inferiores en la tabla (lo mismo) en la tabla es 177.33 repitiéndose, nuevamente cerrado pero ligeramente apagado debido al error de redondeo.

Hemos terminado nuestro trabajo de computar las sumas de cuadrados que necesitamos para poder hacer los siguientes pasos, que incluyen computar los MSE para el efecto y el término de error. Una vez que hacemos eso, podemos encontrar el valor F, que es la relación de las dos MSE.

Antes de hacer eso, es posible que hayas notado que resolvimos para\(SS_\text{Error (left-over)}\), en lugar de calcularlo directamente a partir de los datos. En este capítulo no te vamos a mostrar los pasos para hacer esto. No estamos tratando de ocultar nada, en cambio resulta que estos pasos están relacionados con otra idea importante en ANOVA. Discutimos esta idea, que se llama interacción en el siguiente capítulo, cuando discutimos diseños factoriales (diseños con más de una variable independiente).

 

Calcular los MSE

El cálculo de los MSE (error cuadrático medio) que necesitamos para el\(F\) valor -implica los mismos pasos generales que la última vez. Dividimos cada SS por los grados de libertad para las SS.

Los grados de libertad para\(SS_\text{Effect}\) son los mismos que antes, el número de condiciones - 1. Tenemos tres condiciones, por lo que el df es 2. Ahora podemos calcular el\(MSE_\text{Effect}\).

\[MSE_\text{Effect} = \frac{SS_\text{Effect}}{df} = \frac{72}{2} = 36 \nonumber \]

Los grados de libertad para\(SS_\text{Error (left-over)}\) son diferentes a los anteriores, son los (número de sujetos - 1) multiplicado por el (número de condiciones -1). Tenemos 3 sujetos y tres condiciones, entonces\((3-1) * (3-1) = 2*2 =4\). Quizás se esté preguntando por qué estamos multiplicando estos números. Sostenga ese pensamiento por ahora y espere hasta el siguiente capítulo. Independientemente, ahora podemos calcular el\(MSE_\text{Error (left-over)}\).

\[MSE_\text{Error (left-over)} = \frac{SS_\text{Error (left-over)}}{df} = \frac{177.33}{4}= 44.33 \nonumber \]

 

Compute F

Acabamos de encontrar las dos MSE que necesitamos calcular\(F\). Pasamos por todo esto\(F\) para calcular nuestros datos, así que hagámoslo:

\[F = \frac{MSE_\text{Effect}}{MSE_\text{Error (left-over)}} = \frac{36}{44.33}= 0.812 \nonumber \]

Y, ¡ahí lo tenemos!

 

valor p

Ya realizamos el ANOVA de medidas repetidas usando R y reportamos el ANOVA. Aquí está otra vez. La tabla muestra el\(p\) -valor asociado a nuestro\(F\) -valor.

suppressPackageStartupMessages(library(dplyr))
library(xtable)
scores <- c(20,11,2,6,2,7,2,11,2)
conditions <- as.character(rep(c("A","B","C"), each=3))
subjects <-rep(1:3,3)
means <-c(9.33,8,3.66,9.33,8,3.66,9.33,8,3.66)
diff <-means-mean(scores)
diff_squared <-diff^2
df<-data.frame(subjects,conditions,scores,means,diff, diff_squared)
df$conditions<-as.character(df$conditions)
df$subjects<-as.character(df$subjects)

summary_out <- summary(aov(scores~conditions + Error(subjects/conditions),df[1:9,]))
knitr::kable(xtable(summary_out))

	Df	Suma Cuadrados	Media Cuadrada	Valor F	Pr (>F)
Residuales	2	52.66667	26.33333	NA	F)" style="vertical-align:middle;">NA
condiciones	2	72.00000	36.00000	0.8120301	F)" style="vertical-align:middle;">0.505848
Residuales	4	177.33333	44.33333	NA	F)" style="vertical-align:middle;">NA

Podríamos escribir los resultados de nuestro experimento y decir que la condición de efecto principal no fue significativa, F (2,4) = 0.812, MSE = 44.33, p = 0.505.

¿Qué significa esta afirmación? Recuerde, que el\(p\) -valor representa la probabilidad de obtener el\(F\) valor que observamos o mayor bajo el nulo (suponiendo que las muestras provienen de la misma distribución, el supuesto de que no hay diferencias). Entonces, sabemos que un\(F\) -valor de 0.812 o mayor ocurre con bastante frecuencia por casualidad (cuando no hay diferencias reales), de hecho sucede 50.5% de las veces. En consecuencia, no rechazamos la idea de que cualquier diferencia en los medios que hemos observado podría haberse producido por casualidad.