11.2: Modelos de Muestreo Independientes
- Page ID
- 151865
Primero consideraremos el caso cuando queremos comparar las medias poblacionales de dos poblaciones mediante muestreo independiente.
Distribución de la diferencia de dos medias muestrales
Supongamos que quisiéramos probar la hipótesis\(H_o: \mu_{1}=\mu_{2}\). Tenemos estimadores puntuales para ambos\(\mu_{1}\) y\(\mu_{2}\), es decir\(\overline{X}_1\),\(\overline{X}_1\) y, que tienen aproximadamente Distribuciones Normales bajo el Teorema del Límite Central, pero sería útil combinarlos en un solo estimador. Afortunadamente se sabe que si dos variables aleatorias tienen una Distribución Normal, entonces también lo hace la suma y la diferencia. Por lo tanto, podemos reafirmar la hipótesis como\(H_o: \mu_{1}-\mu_{2}=0\) y utilizar la diferencia de medias muestrales\(\overline{X}_1 - \overline{X}_1\) como estimador puntual para la diferencia en medias poblacionales\(\mu_{1}-\mu_{2}\).
Primero consideraremos el caso cuando queremos comparar las medias poblacionales de dos poblaciones mediante muestreo independiente.
Distribución de la diferencia de dos medias muestrales
Supongamos que quisiéramos probar la hipótesis\(H_o: \mu_{1}=\mu_{2}\). Tenemos estimadores puntuales para ambos\(\mu_{1}\) y\(\mu_{2}\), es decir\(\overline{X}_1\),\(\overline{X}_1\) y, que tienen aproximadamente Distribuciones Normales bajo el Teorema del Límite Central, pero sería útil combinarlos en un solo estimador. Afortunadamente se sabe que si dos variables aleatorias tienen una Distribución Normal, entonces también lo hace la suma y la diferencia. Por lo tanto, podemos reafirmar la hipótesis como\(H_o: \mu_{1}-\mu_{2}=0\) y utilizar la diferencia de medias muestrales\(\overline{X}_1 - \overline{X}_2\) como estimador puntual para la diferencia en medias poblacionales\(\mu_{1}-\mu_{2}\).
\(\mu_{\overline{X}_{1}-\overline{X}_{2}}=\mu_{1-} \mu_{2}\)
\(\sigma_{\overline{X}_{1}-\overline{X}_{2}}=\sqrt{\dfrac{\sigma_{1}^{2}}{n_{1}}+\dfrac{\sigma_{2}^{2}}{n_{2}}}\)
\(Z=\dfrac{\left(\overline{X}_{1}-\overline{X}_{2}\right)-\left(\mu_{1}-\mu_{2}\right)}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\)si\(n_1\) y\(n_2\) son suficientemente grandes.
Comparando dos medias, muestreo independiente: Modelo cuando se conocen las varianzas poblacionales
Cuando se conocen las varianzas poblacionales, el estadístico de prueba para la Hipótesis se\(H_o: \mu_{1}=\mu_{2}\) puede probar con el estadístico de\(Z\) prueba de distribución normal mostrado anteriormente. Además, si tanto el tamaño\(n_1\) de la muestra como\(n_2\) superan los 30, también se puede utilizar este modelo.
Ejemplo: Casas y albercas
¿Las casas más grandes tienen más probabilidades de tener albercas? Los datos de metros cuadrados (tamaño) de viviendas unifamiliares en California se separaron en dos poblaciones: Casas con albercas y casas sin albercas. Contamos con datos de 130 viviendas con albercas y 95 viviendas sin albercas.

Solución
Diseño
Hipótesis de investigación:
\(H_o: \mu_{1} \leq \mu_{2}\)(Las casas con albercas no tienen más metros cuadrados medios)
\(H_a: \mu_{1} > \mu_{2}\)(Las casas con albercas tienen más metros cuadrados medios)
Dado que ambos tamaños de muestra son mayores de 30, el modelo será una \(Z\)prueba de muestra grande comparando dos medias poblacionales con muestreo independiente.
Este modelo es apropiado ya que los tamaños muestrales aseguran que la distribución de la media muestral es aproximadamente Normal a partir del Teorema del Límite Central. Optamos por una prueba de una cola ya que queremos apoyar la afirmación de que los hogares con albercas son más grandes. El estadístico de prueba será\(=\dfrac{\left(\overline{X}_{1}-\overline{X}_{2}\right)-\left(\mu_{1}-\mu_{2}\right)}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\)
El error tipo I sería rechazar la Hipótesis Nulo y reclamar casa con albercas son más grandes, cuando no son más grandes. Se decidió limitar este error estableciendo el nivel de significancia (\(\alpha\)) a 1%.
La regla de decisión bajo el método del valor crítico sería rechazar la Hipótesis Null cuando el valor del estadístico de prueba se encuentre en la región de rechazo. En otras palabras, rechazar\(H_o\) cuándo\(Z > 2.326\). La decisión bajo el método\(p\) ‐value es rechazar\(H_o\) si el\(p\) ‐valor es <\(\alpha\).
Datos/Resultados

Dado que el estadístico de prueba (\(Z = 4.19\)) es mayor que el valor crítico (2.326),\(H_o\) se rechaza. También el\(p\) ‐valor (0.000013) es menor que\(\alpha\) (0.01), la decisión es Rechazar\(H_o\).
Conclusión
El investigador hace la fuerte declaración de que las casas con albercas tienen un metraje medio significativamente mayor que el hogar sin albercas.
Modelo cuando se desconocen las varianzas poblacionales, pero se supone que son iguales
En el caso de que se desconozcan las desviaciones estándar de la población, parece lógico simplemente reemplazar las desviaciones estándar poblacionales para cada población con las desviaciones estándar de la muestra y usar una\(t\) distribución como la que hicimos para el caso de una población. Sin embargo, esto no es tan simple cuando el tamaño de la muestra para cualquiera de los grupos es menor de 30
Consideraremos dos modelos. Este primer modelo (que preferimos usar ya que tiene más potencia) asume que las varianzas poblacionales son iguales y se llama la varianza agrupada\(t\) ‐test. En este modelo combinamos o “agrupamos” las dos desviaciones estándar de la muestra en una sola estimación llamada desviación estándar agrupada,\(s_p\). Si el teorema del límite central está funcionando, entonces podemos sustituir\(s_1\) y\(s_p\)\(s_2\) obtener\(t\) una distribución con\(n_{1}+n_{2}-2\) grados de libertad:
Supuestos de modelo
- Muestreo Independiente
- \(\overline{X}_{1}-\overline{X}_{2}\)aproximadamente Normal
- \(\sigma_{1}^{2}=\sigma_{2}^{2}\)
Estadístico de prueba
- \(t=\dfrac{\left(\overline{X}_{1}-\overline{X}_{2}\right)-\left(\mu_{1}-\mu_{2}\right)}{s_{p} \sqrt{\frac{1}{n_{1}}+\frac{1}{n_{2}}}}\)
- \(s_{p}=\sqrt{\dfrac{\left(n_{1}-1\right) s_{1}^{2}-\left(n_{2}-1\right) s_{2}^{2}}{n_{1}+n_{2}-2}}\)
- Grados de libertad\(=n_{1}+n_{2}-2\)
Ejemplo: Economía de combustible
Un estudio reciente de la EPA comparó la economía de combustible en carretera de los turismos nacionales e importados. Una muestra de 15 autos domésticos reveló una media de 33.7 MPG (milla por galón) con una desviación estándar de 2.4 mpg. Una muestra de 12 automóviles importados reveló una media de 35.7 mpg con una desviación estándar de 3.9. En el nivel de significancia .05 ¿puede la EPA concluir que el MPG es mayor para los autos importados?

Solución
Diseño
Lo mejor es asociar el subíndice 2 con el grupo de control; en este caso dejaremos que los autos nacionales sean población 2.
Hipótesis de investigación:
\(H_o: \mu_{1} \leq \mu_{2}\)(Los autos compactos importados no tienen un MPG medio más alto)
\(H_a: \mu_{1} > \mu_{2}\)(Los autos compactos importados tienen un MPG medio más alto)
Supondremos que las varianzas poblacionales son iguales\(\sigma_{1}^{2}=\sigma_{2}^{2}\), por lo que el modelo será una \(t\)prueba de varianza agrupada. Este modelo es apropiado si la distribución de las diferencias de medias muestrales es aproximadamente Normal a partir del Teorema del Límite Central. Se selecciona una prueba de una cola en función de\(H_a\).
El error tipo I sería rechazar la Hipótesis Null y afirmar que las importaciones tienen un MPG medio más alto, cuando no tienen MPG más alto. La prueba se ejecutará a un nivel de significancia (\(\alpha\)) del 5%.
Los grados de libertad para esta prueba son 25, por lo que la regla de decisión bajo el método del valor crítico sería rechazar\(H_o\) cuándo\(t > 1.708\). La decisión bajo el método\(p\) ‐value es rechazar\(H_o\) si el\(p\) ‐valor es <\(\alpha\).
Datos/Resultados
\(s_{p}=\sqrt{\dfrac{(12-1) 3.86^{2}-(12-1) 2.16^{2}}{15+12-2}}=3.03\)
\(t=\dfrac{(35.76-33.59)-0}{3.03 \sqrt{\frac{1}{12}+\frac{1}{15}}}=1.85\)
Desde 1.85 > 1.708, la decisión sería Rechazar\(H_o\). También se calcula que el valor p‐es .0381 lo que nuevamente muestra que el resultado es significativo en el nivel del 5%.
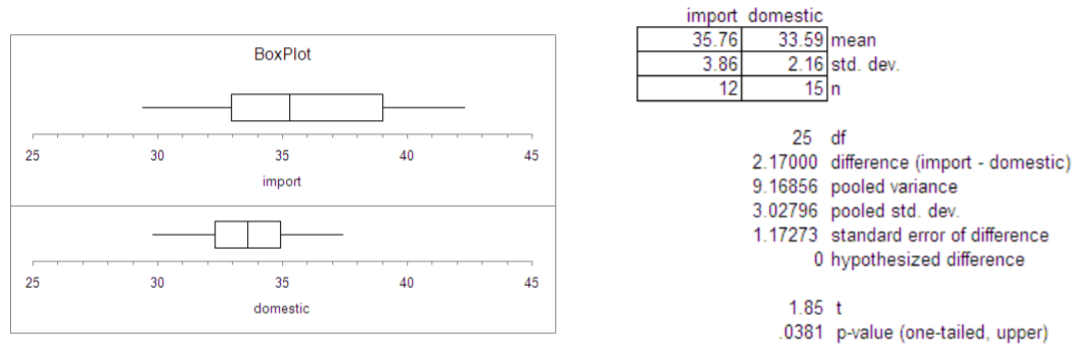
Conclusión
Los autos compactos importados tienen una calificación promedio de MPG significativamente más alta en comparación con los autos nacionales
Modelo cuando se desconocen varianzas poblacionales, pero se supone que son desiguales
En el ejemplo anterior, asumimos que las varianzas poblacionales eran iguales. No obstante, al observar la gráfica de caja de los datos o las desviaciones estándar de la muestra, parece que los autos de importación tienen más variabilidad MPG que los automóviles nacionales, lo que violaría el supuesto de varianzas iguales requeridas para la prueba de Varianza agrupada\(t\) ‐test.
Afortunadamente, existe un modelo alternativo que se ha desarrollado para cuando las varianzas poblacionales son desiguales, llamado modelo de Behrens‐Fisher 81, o la prueba de varianzas desiguales\(t\) ‐test.
Supuestos de modelo
- Muestreo Independiente
- \(\overline{X}_{1}-\overline{X}_{2}\)aproximadamente Normal
- \(\sigma_{1}^{2} \neq \sigma_{2}^{2}\)
Estadístico de prueba
- \(t^{\prime}=\dfrac{\left(\bar{X}_{1}-\bar{X}_{2}\right)-\left(\mu_{1}-\mu_{2}\right)}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\)
- \(d f=\dfrac{\left(\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}\right)^{2}}{\left[\frac{\left(s_{1}^{2} / n_{1}\right)^{2}}{\left(n_{1}-1\right)}+\frac{\left(s_{2}^{2} / n_{2}\right)^{2}}{\left(n_{2}-1\right)}\right]}\)
Los grados de libertad serán menores o iguales a\(n_{1}+n_{2}-2\), por lo que esta prueba generalmente tendrá menos potencia que la varianza agrupada\(t\) ‐test.
Ejemplo: Economía de combustible
Repetiremos el ejemplo anterior para ver si podemos apoyar la afirmación de que los autos compactos importados tienen MPG promedio más altos en comparación con los autos compactos nacionales. Esta vez asumiremos que las varianzas poblacionales no son iguales.
Solución
Diseño
Nuevamente vamos a dejar que los autos nacionales sean población 2.
Hipótesis de investigación:
\(H_o: \mu_{1} \leq \mu_{2}\)(Los autos compactos importados no tienen un MPG medio más alto)
\(H_a: \mu_{1} > \mu_{2}\)(Los autos compactos importados tienen un MPG medio más alto)
Supondremos que las varianzas poblacionales son desiguales\(\sigma_{1}^{2} \neq \sigma_{2}^{2}\), por lo que el modelo será una varianza desigual\(t\) ‐test. Este modelo es apropiado si la distribución de las diferencias de medias muestrales es aproximadamente Normal a partir del Teorema del Límite Central. Se selecciona una prueba de una cola en función de\(H_a\).
El error de tipo I sería rechazar la Hipótesis Null y afirmar que las importaciones tienen un MPG medio más alto, cuando no tienen MPG más alto. La prueba se ejecutará a un nivel de significancia (\(\alpha\)) del 5%. Los grados de libertad para esta prueba son 16 (ver cálculo a continuación), por lo que la regla de decisión bajo el método del valor crítico sería rechazar\(H_o\) cuándo\(t > 1.746\). La decisión bajo el método\(p\) ‐value es rechazar\(H_o\) si el\(p\) ‐valor es <\(\alpha\)
Datos/Resultados

\(d f=\dfrac{\left(\frac{2.16^{2}}{15}+\frac{3.86^{2}}{12}\right)^{2}}{\left[\frac{\left(2.16^{2} / 15\right)^{2}}{(15-1)}+\frac{\left(3.86^{2} / 12\right)^{2}}{(12-1)}\right]}=16\)
\(t=\dfrac{(35.76-33.59)-0}{\sqrt{\frac{2.16^{2}}{15}+\frac{3.86^{2}}{12}}}=1.74\)
Desde 1.74 <1.746, la decisión sería No Rechazar\(H_o\). También se calcula que el\(p\) valor ‐es .0504 lo que nuevamente muestra que el resultado no es significativo (apenas) al nivel del 5%.
Conclusión
Evidencia insuficiente para afirmar que los autos compactos importados tienen una calificación promedio de MPG significativamente más alta en comparación con los automóviles nacionales.
Se puede ver la menor potencia de esta prueba cuando se compara con la varianza agrupada\(t\) ‐ejemplo de prueba donde Ho fue rechazado. Siempre preferimos ejecutar la prueba con mayor potencia cuando sea apropiado.


